Study on Partial Differential Equations and 3D Printing

When Partial Differential Equations and Neural Networks Meet 3D Printing: A Case Study of 3D Printing of PINN Solutions
Tianwei Li, Ruike Li
Article ID: 102731
2023 China Automation Congress (CAC)

Abstract
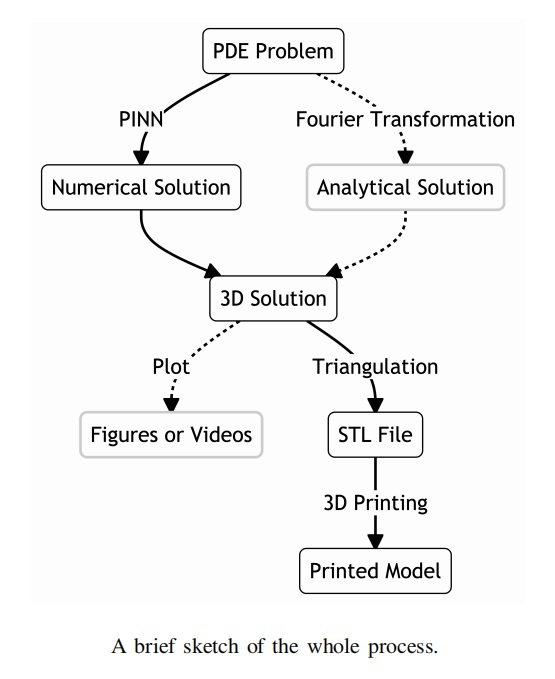
In the past decades, the PDE and the 3D printing communities have developed rapidly in parallel. However, surprisingly, they have very little interaction. The PDE-based 3D printing technique is almost the only reported combination that uses PDE to model and optimize the behavior of materials during the printing process. In this paper, we propose another application that also bridges the gap between the PDE community and the 3D printing community by 3D-printing the numerical solutions of PDE for educational purposes. 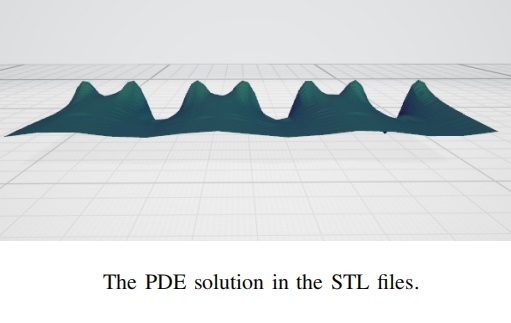Specifically, we apply the PINN technique to solve the PDE with initial conditions and boundary conditions, export it as a STL file through triangulation, and feed it to the 3D printer for printing. Numerical simulations and experiments have verified the process.The scheme may be enjoyably used for educational demonstration and scientific art.

Index Terms
Physics-informed neural network, Partial differential equations, 3D printing.