图

主讲教师

李辉

图论简介

图论以图为研究对象, 在计算机科学、运筹学、系统科学和数学中有重要地位.

一个图就是一个离散的拓扑结构, 经常用于描述和研究许多领域中的问题.

图论中的图是由若干给定的点及连接两点的线所构成的图形, 这种图形通常用来描述某种事物之间的特定关系. 用点代替事物, 用两点之间的线代表相应两事物之间具有的各种关系.

几个图论的经典问题:

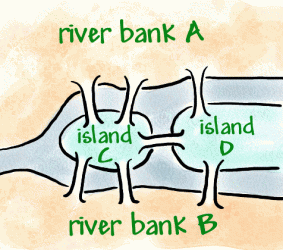
问题一: 哥尼斯堡七桥问题 (The Konigsberg Bridge Problem, https://nrich.maths.org/2484)

问题二: 哈密尔顿环球旅行问题 (Hamiltonian path problem)

问题三: 四色问题 (Four color theorem)

问题四: 旅行商问题 (Travelling salesman problem)

哥尼斯堡七桥问题: 从这四片陆地中任何一片出发, 仅通过每座桥一次, 回到起点.

哈密尔顿环球旅行问题: 从一个节点出发, 经过每个节点恰好1次, 然后回到出发点.

四色问题: 对任何一张地图进行着色, 两个共同边界的区域染不同的颜色, 则只需四种颜色就足够.

图的基本概念

图的定义

定义: 设\(A\)和\(B\)是任意两个集合, 称 \[A\&B=\{(a, b)|a{\in}A, b{\in}B\}\] 为\(A\)与\(B\)的无序积.\((a, b)\)称为无序偶.

对于无序偶, 有\((a, b)=(b, a)\).

例: 设\(A=\{a, b\}\), \(B=\{1, 2\}\), 则

\[A\&B=\{(a, 1), (a, 2), (b, 1), (b, 2)\}=\{(1, a), (a, 2), (b, 1), (b, 2)\}\] \[(a, 1)=(1, a), (a, 2)=(2, a), {\cdots}\]

图分为无向图、有向图和混和图三类.

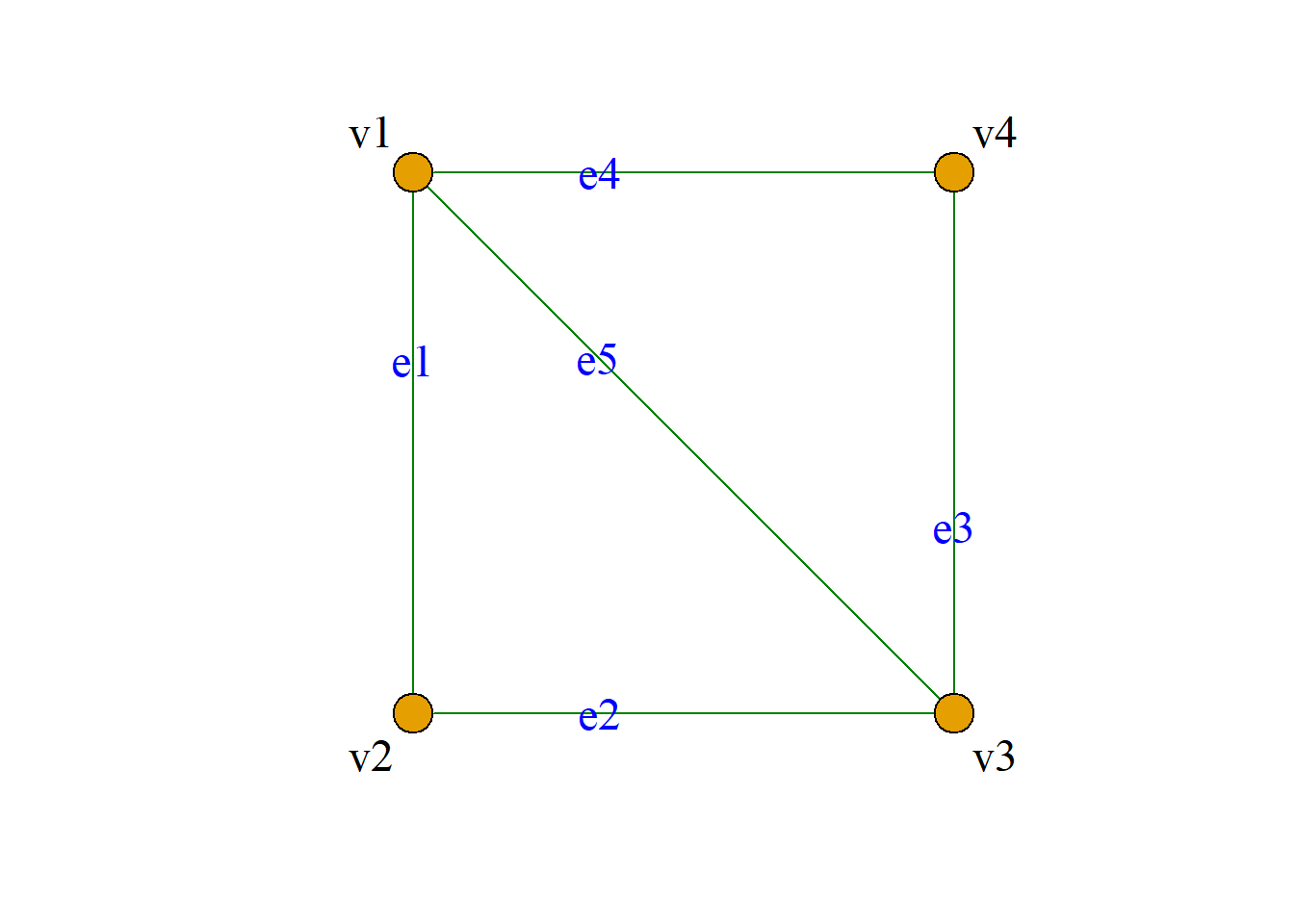
定义: 一个无向图是一个三元组\(G={\langle}V, E, \varphi{\rangle}\). 其中:

\(V\)是一个非空有限集合, 它的元素称为结点(节点, 顶点).
\(E\)是一个有限集合, 它的元素称为无向边.
\(\varphi\)是从边集\(E\)到结点集\(V\)上的无序偶映射

(即\(\varphi:E{\rightarrow}V\&V\)).

通常是用平面上的图形来表示无向图

\(G={\langle}V, E, {\varphi}{\rangle}\), 称为无向图的图示.

\(V\)中的每个结点用一个小圆圈(小圆点)来表示, \(E\)中的每条边用连接它的两个端点的直线或曲线来表示.

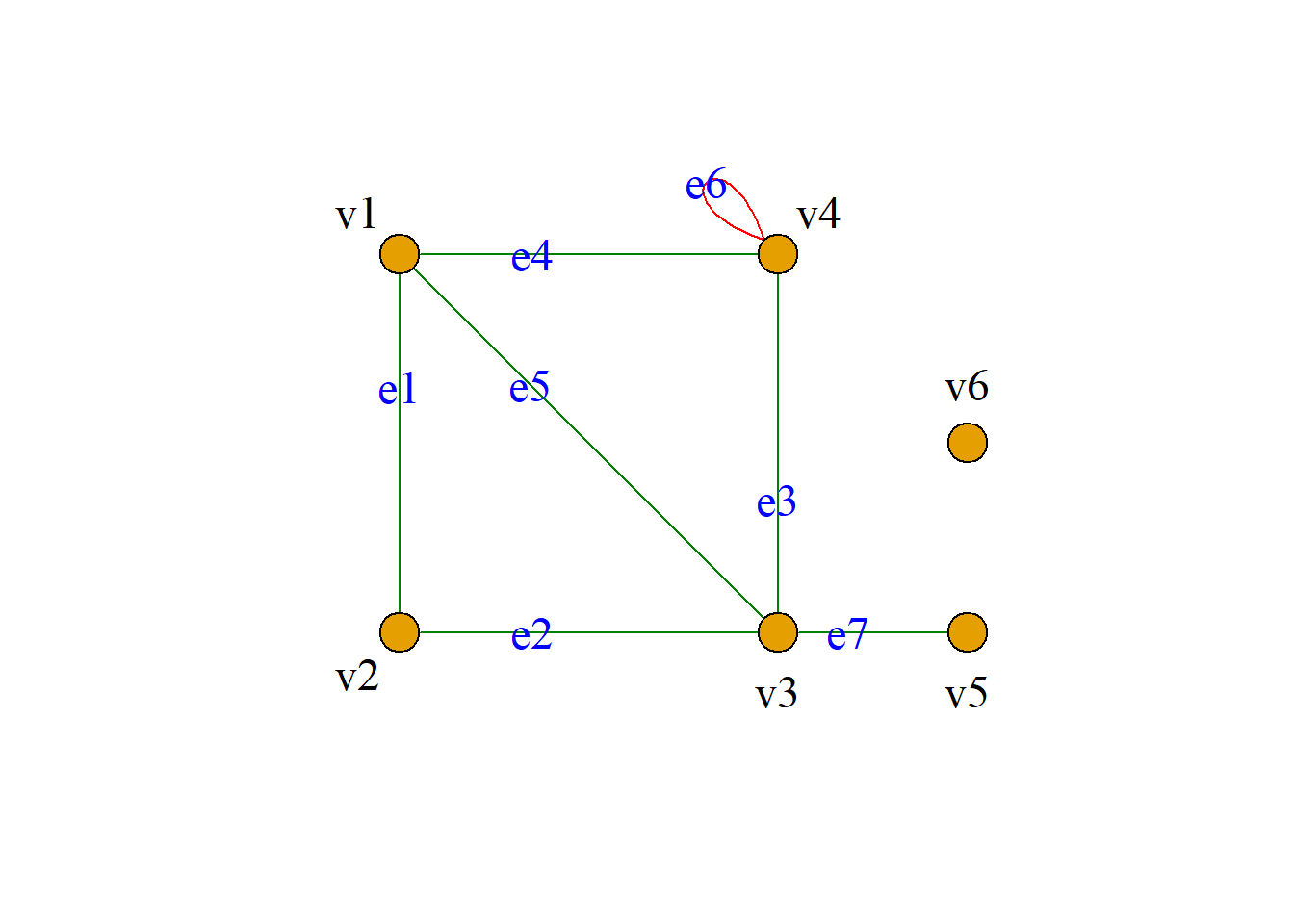
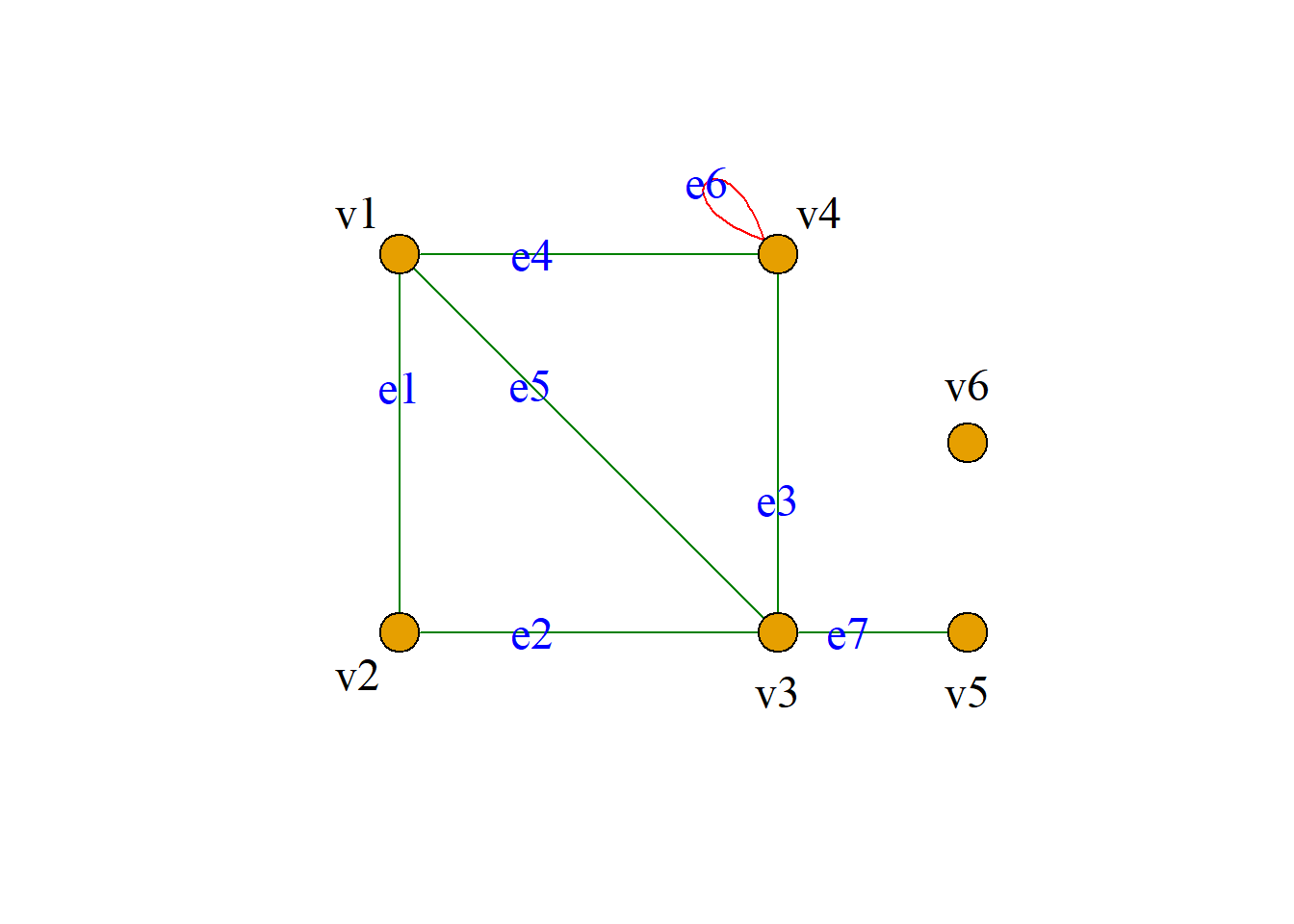
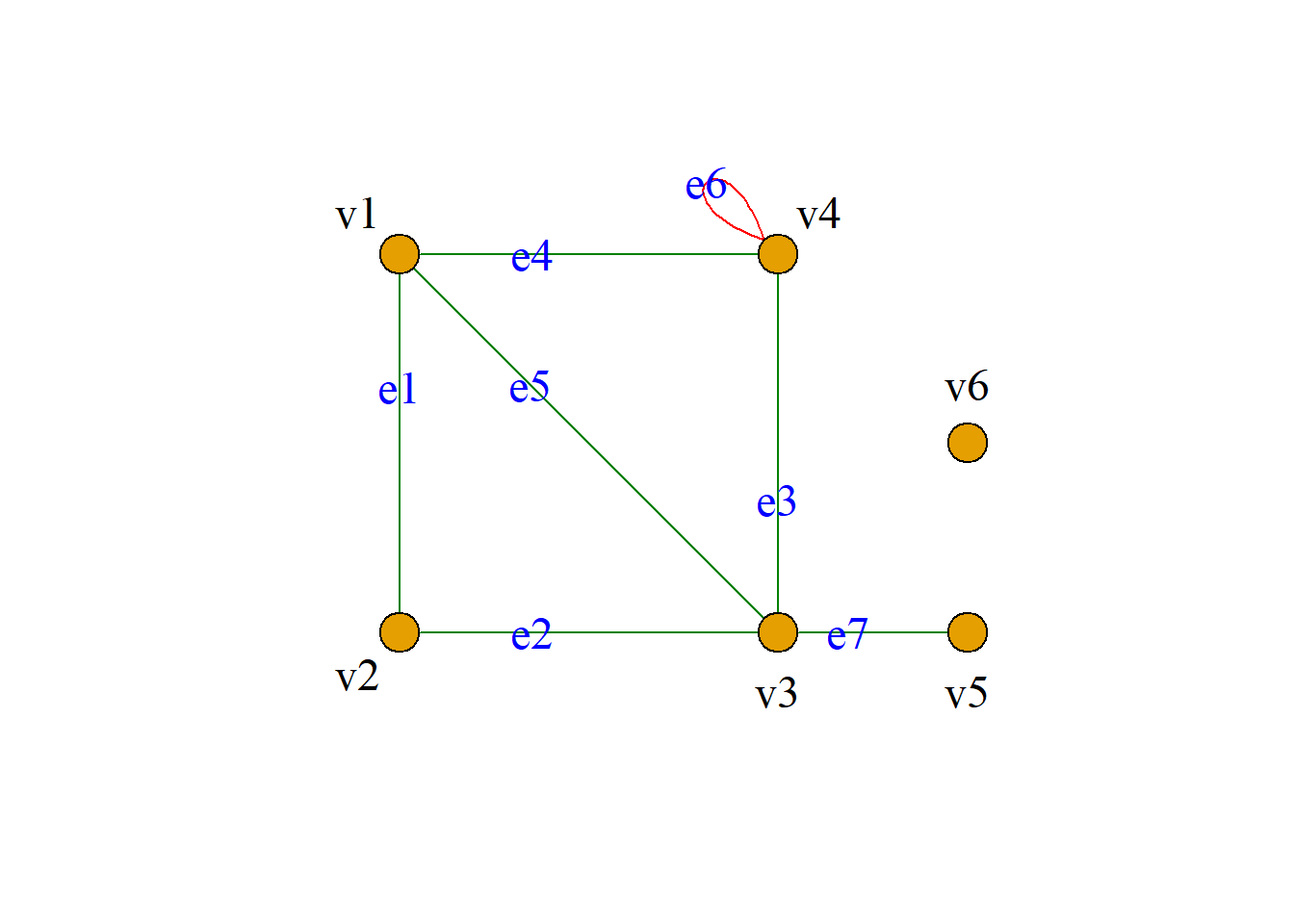
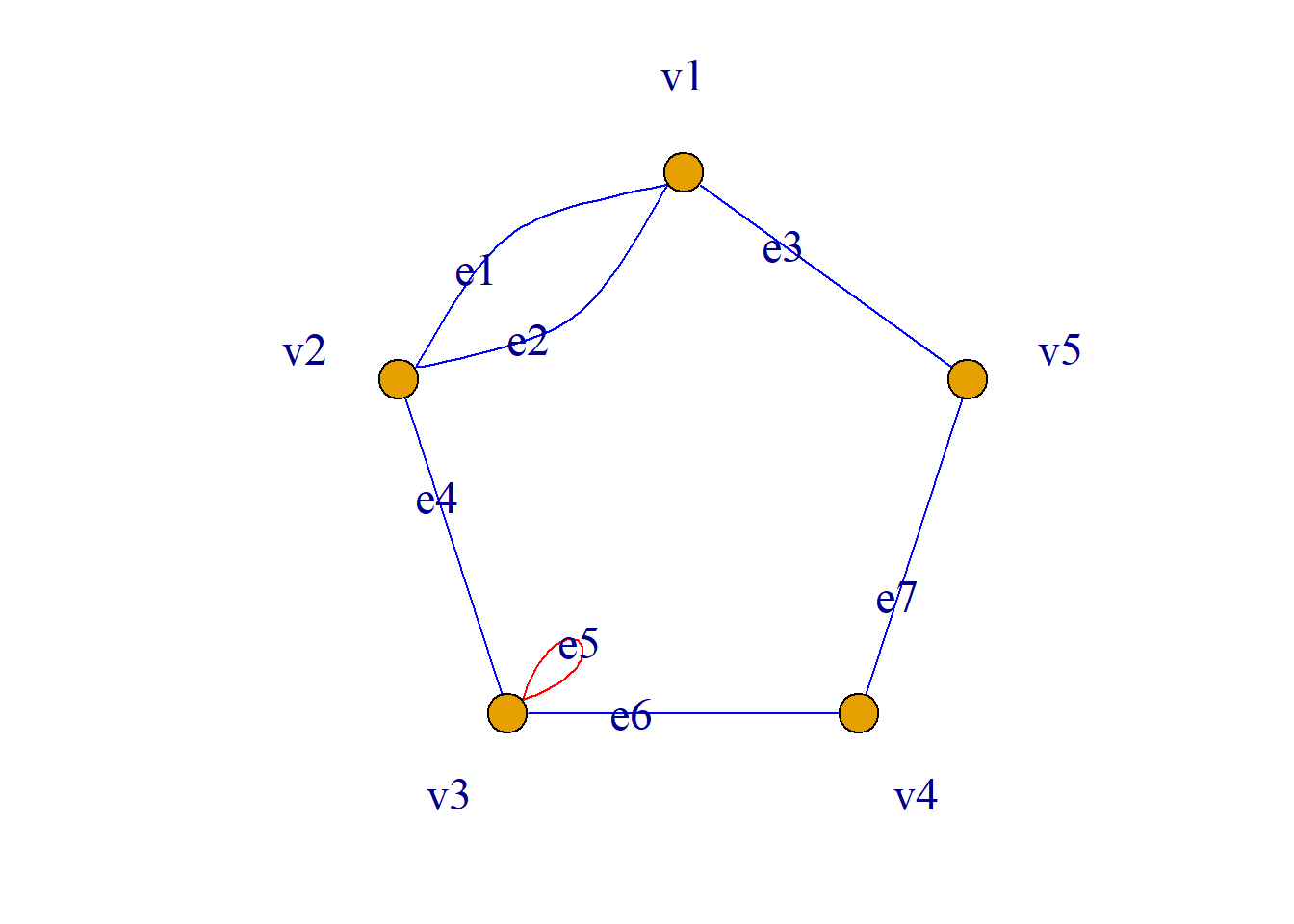
例: 无向图\(G={\langle}V, E, {\varphi}{\rangle}\), 其中:

\[V=\{v_1, v_2, v_3, v_4, v_5, v_6\},\] \[E=\{e_1, e_2, e_3, e_4, e_5, e_6, e_7\}.\] \[{\varphi}(e_1)=(v_1, v_2),\,\,{\varphi}(e_2)=(v_2, v_3)\] \[{\varphi}(e_3)=(v_3, v_4),\,\,{\varphi}(e_4)=(v_1, v_4)\] \[{\varphi}(e_5)=(v_1, v_3),\,\,{\varphi}(e_6)=(v_4, v_4)\] \[{\varphi}(e_7)=(v_3, v_5)\] 简化表示: \[V=\{v_1, v_2, v_3, v_4, v_5, v_6\}, \] \[E=\{(v_1, v_2), (v_2, v_3), (v_3, v_4), (v_1, v_4),\] \[(v_1, v_3), (v_4, v_4), (v_3, v_5)\}\]

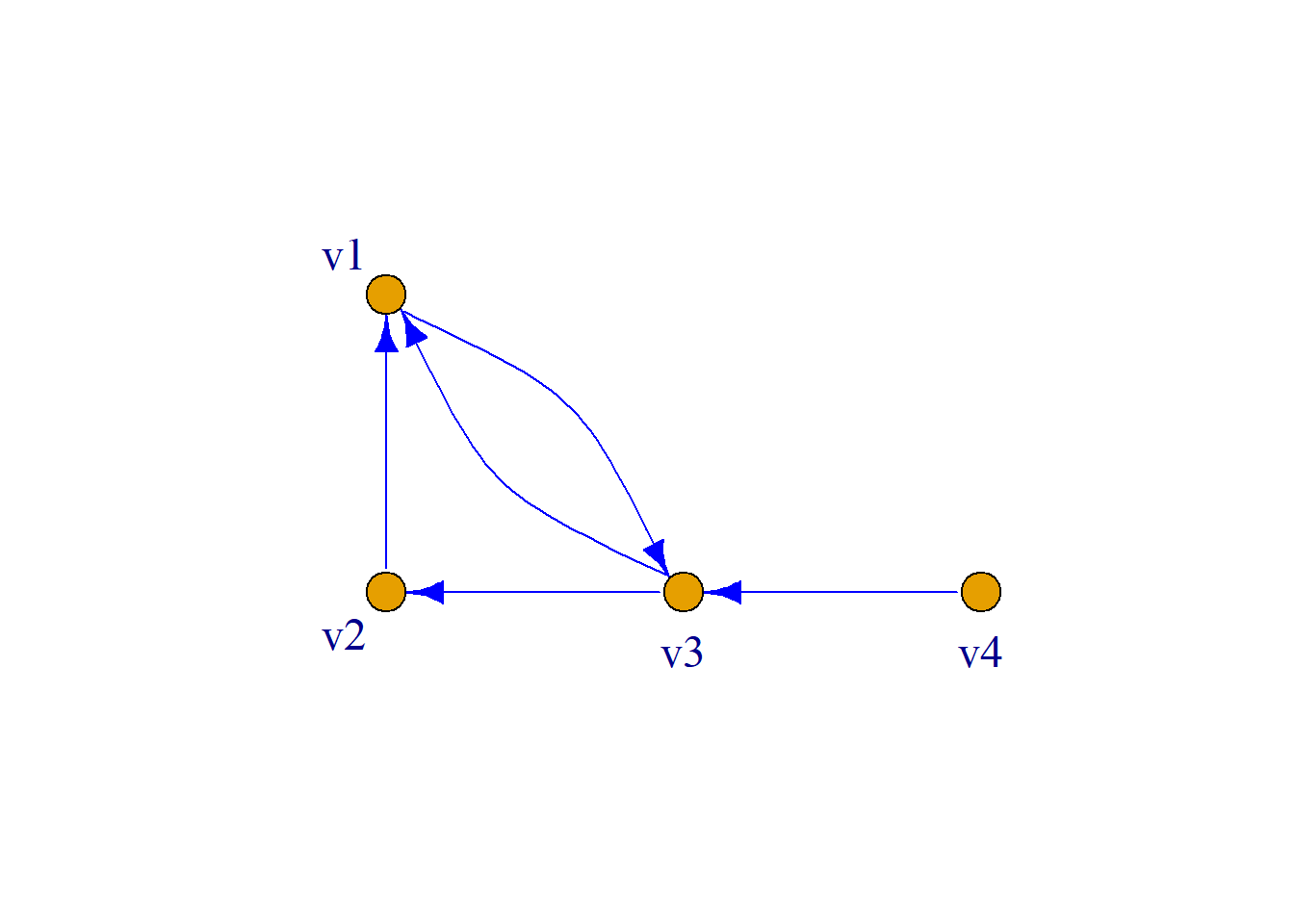
定义: 一个有向图是一个三元组\(G={\langle}V, E, {\varphi}{\rangle}\).

其中:

\(V\)是一个非空有限集合, 它的元素称为结点(节点, 顶点).
\(E\)是一个有限集合, 它的元素称为有向边.
\({\varphi}\)是从边集E到结点集\(V\)上的有序偶映射

(即\({\varphi}:E{\rightarrow}V{\times}V)\).

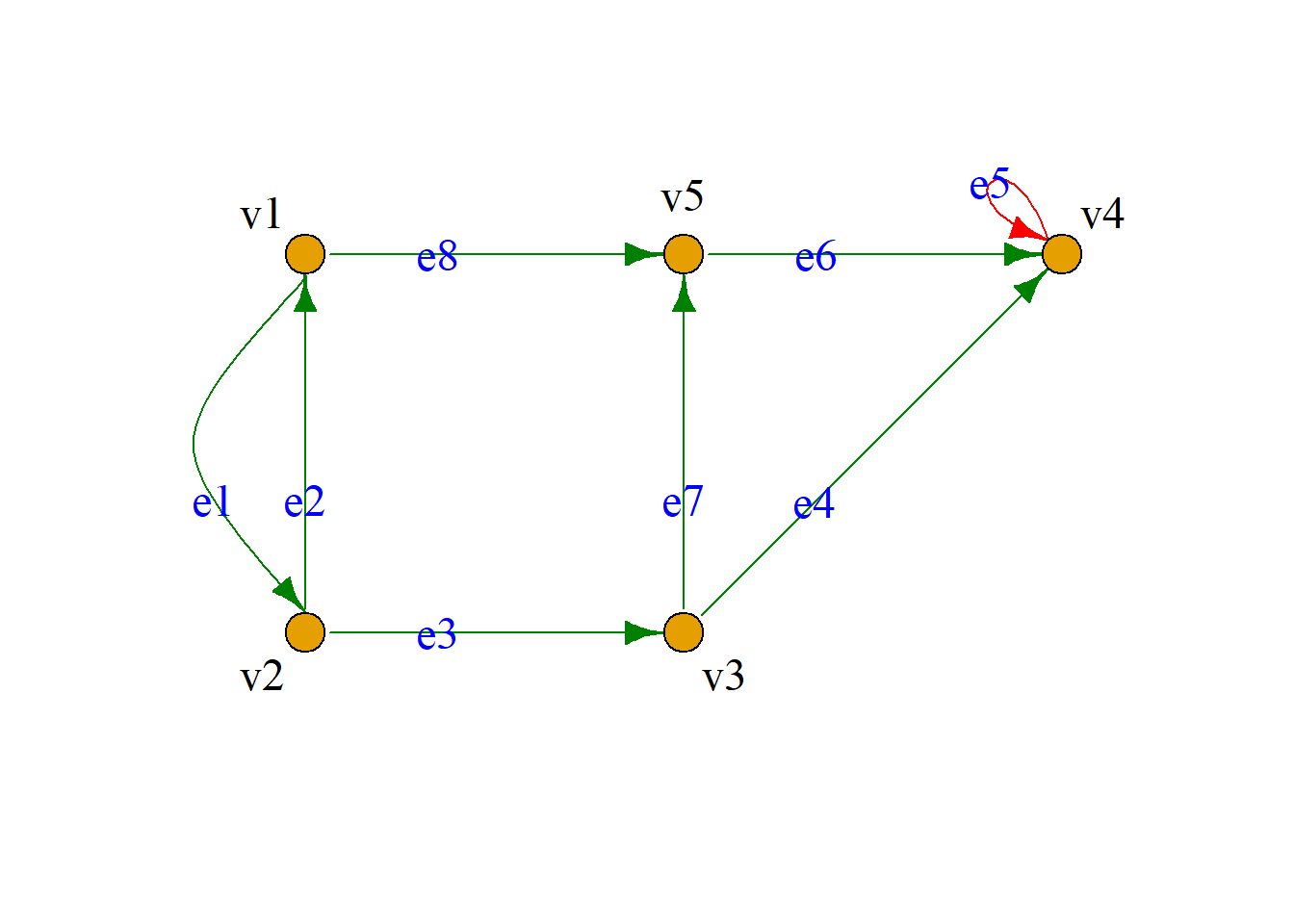
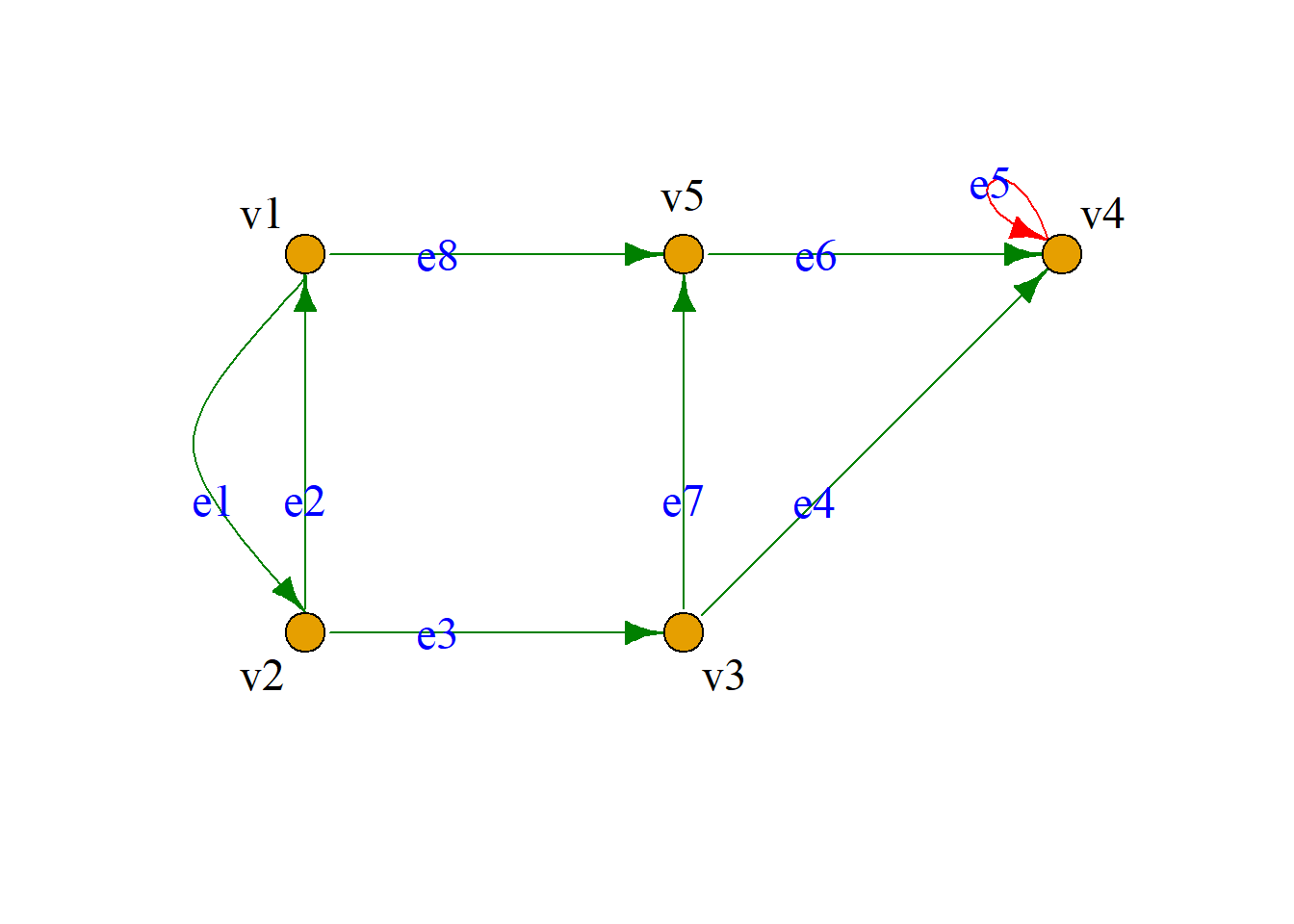
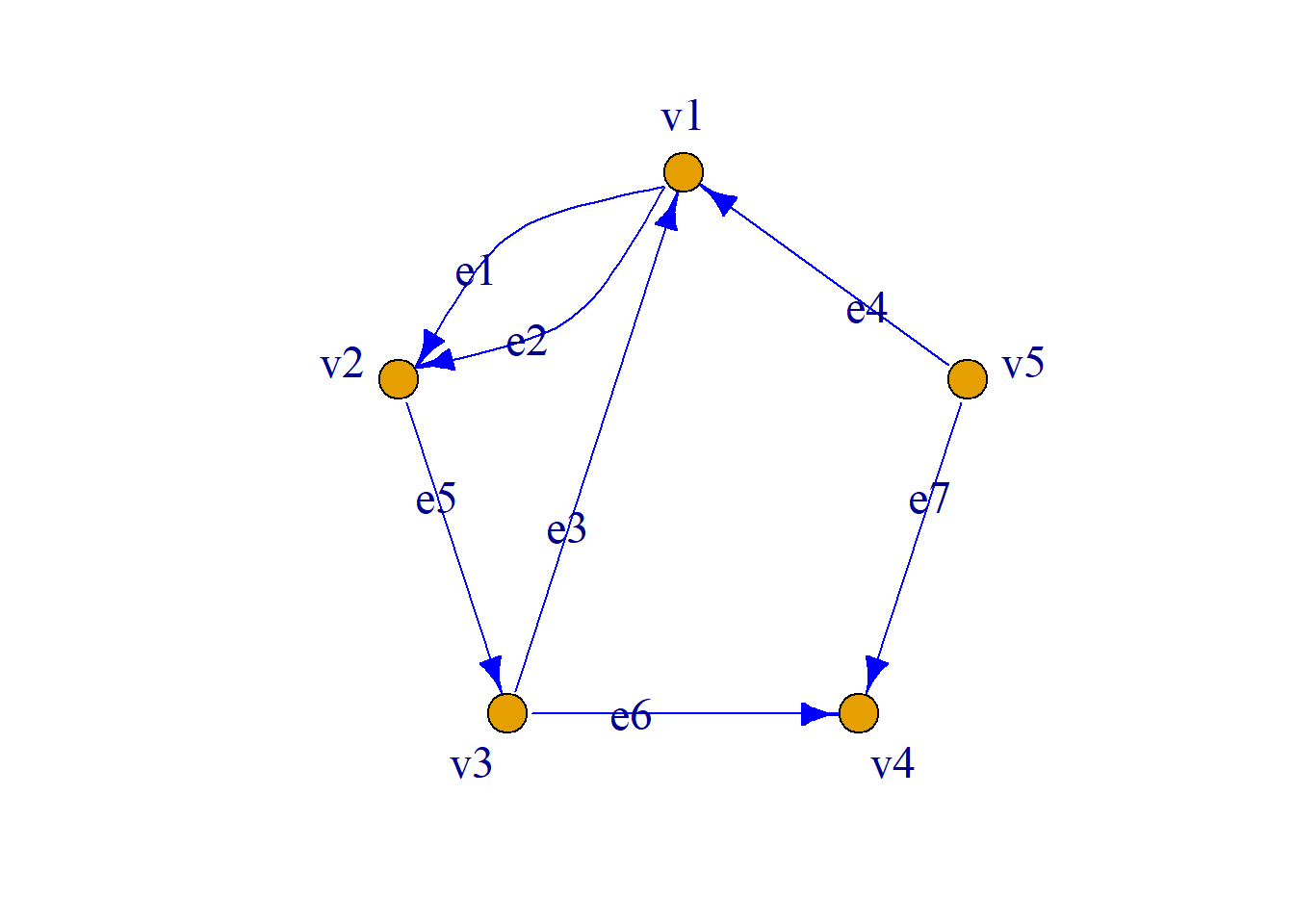
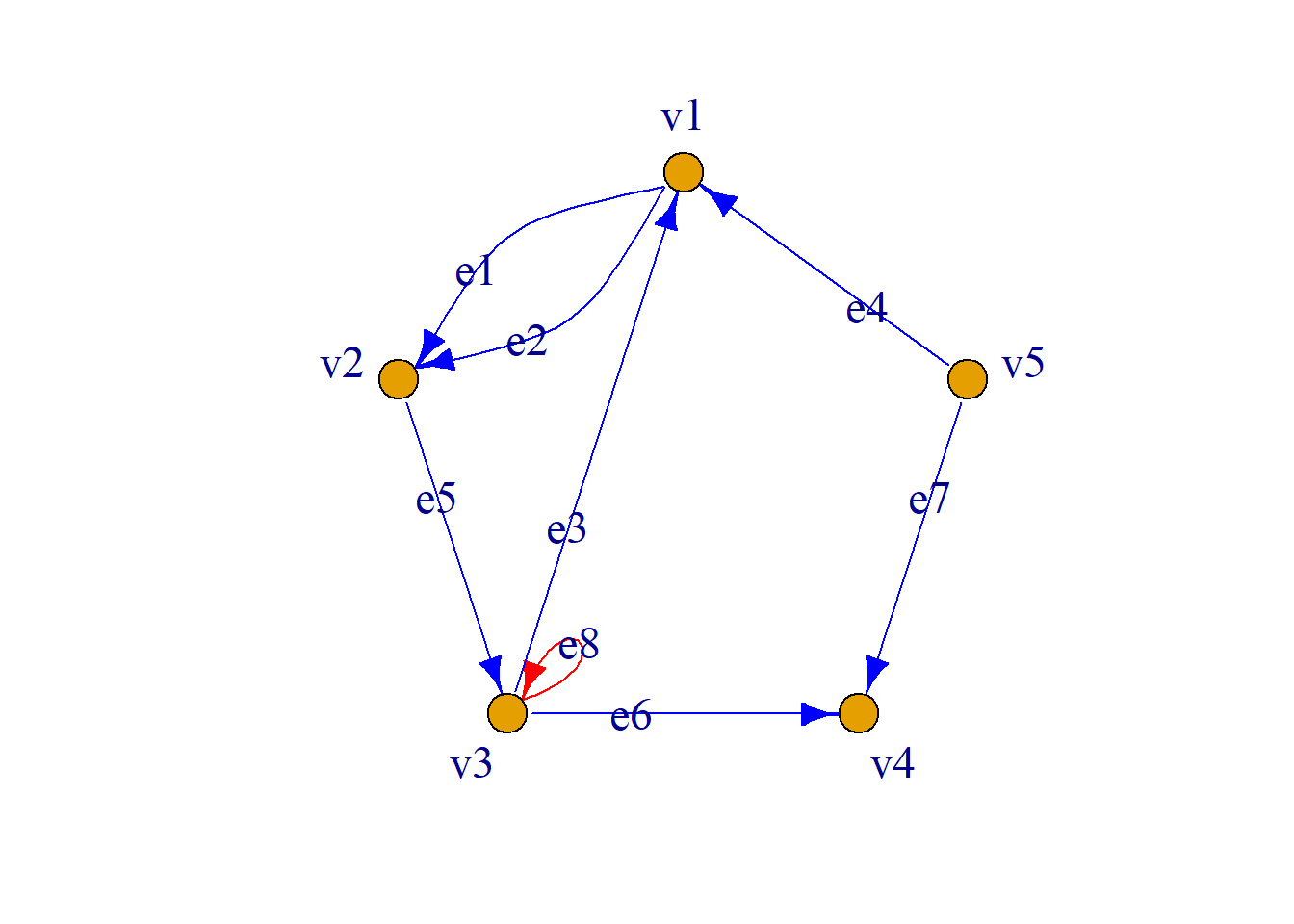
例: 有向图\(G={\langle}V, E, {\varphi}{\rangle}\), \(V=\{v_1, v_2, v_3, v_4, v_5\}\)

\[E=\{e_1, e_2, e_3, e_4, e_5, e_6, e_7, e_8\}\] \[{\varphi}(e_1)={\langle}v_1, v_2{\rangle},\,\,{\varphi}(e_2)={\langle}v_2, v_1{\rangle}\] \[{\varphi}(e_3)={\langle}v_2, v_3{\rangle},\,\,{\varphi}(e_4)={\langle}v_3, v_4{\rangle}\] \[{\varphi}(e_5)={\langle}v_4, v_4{\rangle},\,\,{\varphi}(e_6)={\langle}v_5, v_4{\rangle}\] \[{\varphi}(e_7)={\langle}v_3, v_5{\rangle},\,\,{\varphi}(e_8)={\langle}v_1, v_5{\rangle}\]

简化表示: \[V=\{v_1, v_2, v_3, v_4, v_5\}\] \[E=\{{\langle}v_2, v_1{\rangle}, {\langle}v_1, v_2{\rangle}, {\langle}v_2, v_3{\rangle}, {\langle}v_3, v_4{\rangle}, \] \[{\langle}v_4, v_4{\rangle}, {\langle}v_5, v_4{\rangle}, {\langle}v_3, v_5{\rangle}, {\langle}v_1, v_5{\rangle}\}\]

进一步简化: \(G={\langle}5, 8{\rangle}\)

图的相关术语

定义: 对于无向图, 若边\(e\)与结点的无序偶\((v_i, v_j)\)相联系, 则称结点\(v_i\)和\(v_j\)是\(e\)的端点, 记为\(e=(v_i, v_j)\), 并称\(e\)关联结点\(v_i\)和\(v_j\), 结点\(v_i\)和\(v_j\)为邻接点.

关联同一个结点的两条边称为邻接边.

一条边关联的两个结点若相同, 称之为环.

例: \(e_1=(v_1, v_2), v_1, v_2\)为\(e_1\)的端点, \(e_1\)关联结点\(v_1\)和\(v_2\), \(v_1\)和\(v_2\)称为邻接点, \(e_3\)和\(e_4\)称为邻接边. \(e_6\)为环.

定义: 在无向图中, 对于任意结点\(v\)而言, 关联\(v\)的边的数目称为\(v\)的度, 记为\(d(v)\)(\(deg(v)\)).若结点\(v\)上有环, 该结点的度因环而增加1.

例: 图\(G\)中, 各结点的度分别为:

\[d(v_1)=3, d(v_2)=2, \] \[d(v_3)=4, d(v_4)=4, \] \[d(v_5)=1, d(v_6)=0.\]

定义: 对于有向图, 若边\(e\)与结点有序偶\({\langle}v_i, v_j{\rangle}\)相联系, 则称结点\(v_i\)和\(v_j\)是\(e\)的端点, 记为\(e={\langle}v_i, v_j{\rangle}\), 并称\(v_i\)为\(e\)的始点, \(v_j\)为\(e\)的终点, \(v_i\)邻接到\(v_j\), \(v_j\)邻接于\(v_i\), \(e\)关联结点\(v_i\)和\(v_j\), 结点\(v_i\)和\(v_j\)为邻接结点.

关联同一个结点的两条边称为邻接边.

例: \(e_2={\langle}v_3, v_1{\rangle}\);\(v_1\), \(v_3\)为\(e_2\)的端点;\(v_3\)为\(e_2\)的始点, \(v_1\)为\(e_2\)的终点;\(e_2\)关联结点\(v_1\)和\(v_3\);\(v_1\)和\(v_3\)称为邻接点, \(e_1\)和\(e_3\)称为邻接边.

定义: 在有向图中, 对于任意结点\(v\)而言, 以\(v\)为始点的边的数目, 称为\(v\)的出度, 记为\(d^+(v)\).

以\(v\)为终点的边的数目, 称为\(v\)的入度, 记为\(d^-(v)\).

结点的出度与入度之和, 称为结点\(v\)的度, 记为\(d(v)\).

显然\(d(v)=d^+(v)+d^-(v).\)

若结点\(v\)上有环, 该结点的出度和入度因环而各增加1.

例: 如图, 各结点的度分别为:

\[d(v_1)=d^+(v_1)+d^-(v_1)=2+1=3\] \[d(v_2)=d^+(v_2)+d^-(v_2)=2+1=3\] \[d(v_3)=d^+(v_3)+d^-(v_3)=2+1=3\] \[d(v_4)=d^+(v_4)+d^-(v_4)=1+3=4\] \[d(v_5)=d^+(v_5)+d^-(v_5)=1+2=3\]

度为1的结点称为悬挂点.

图中\(v_5\)是悬挂点.

度为0的结点称为孤立点.

图中\(v_6\)是孤立点.

孤立点是无边关联的结点.

定义: 对于图\(G={\langle}V, E{\rangle}\), 记

\[\Delta(G)=max\{d(v)|v{\in}V\}\] \[\delta(G)=min\{d(v)|v{\in}V\}\]

分别称为图\(G={\langle}V, E{\rangle}\)的最大度和最小度. 图中: \[\Delta(G)=4\] \[\delta(G)=0.\]

有些图只有孤立点, 这类图称为零图.

特别地, 仅由一个孤立点组成的图称为平凡图.

显然, 在零图和平凡图中只有结点而没有边.

定理(握手定理): 在任何图\(G={\langle}V, E{\rangle}\)(有向图或无向图)中, 各结点的度之和等于边数的两倍, 即:

\[\sum_{v{\in}V}d(v)=2m\] 其中, \(m=|E|\)为图\(G\)的边数.

证明: 因为每条边关联两个结点(环关联一个结点两次), 故每条边为结点的度之总和提供两度, \(m\)条边共提供\(2m\)度, 这意味着各结点度的总和是边数目的两倍.

定理: 在任何图\(G={\langle}V, E{\rangle}\)中, 度为奇数的结点个数必为偶数.

证明: 设\(v_1\)和\(v_2\)分别是图中偶数度结点和奇数度结点的集合, 于是由有 \[\sum_{v{\in}V_1}d(v)+\sum_{v{\in}V_2}d(v)=\sum_{v{\in}V}d(v)=2m\] 式中\(2m\)和\(\sum_{v{\in}V_1}d(v)\)均是偶数, 所以, \(\sum_{v{\in}V_2}d(v)\)也是偶数.

又因为和式\(\sum_{v{\in}V_2}d(v)\)中的每一项均为奇数, 故其项数必为偶数.

例: 问是否存在含有6个结点, 度分别为: 1, 2, 3, 4, 2, 1的无向图？

解: 不存在这样的无向图. 因为如果存在这样的以1, 2, 3, 4, 2, 1为结点度的无向图, 则该图奇度结点的个数为3, 是一个奇数.

定理: 在任何有向图\(G={\langle}V, E{\rangle}\)中, 各结点的出度之和等于各结点的入度之和, 即: \[\sum_{v{\in}V}d^+(v)=\sum_{v{\in}V}d^-(v)=m\] 其中, \(m=|E|\)为图\(G\)的边数.

证明: 每条有向边都有一个始点和一个终点, 即每条有向边对应一个出度和一个入度, 所以\(m\)条有向边必产生\(m\)个出度和\(m\)个入度.

这\(m\)个出度和\(m\)个入度就是图中所有结点的出度之和与入度之和.

因此, 在有向图中, 各结点的出度之和等于各结点的入度之和, 都等于边的数目.

定义: 各结点的度均相同的图称为正则图. 各结点的度均为\(k\)的正则图称为k度正则图, 记作k-正则图.

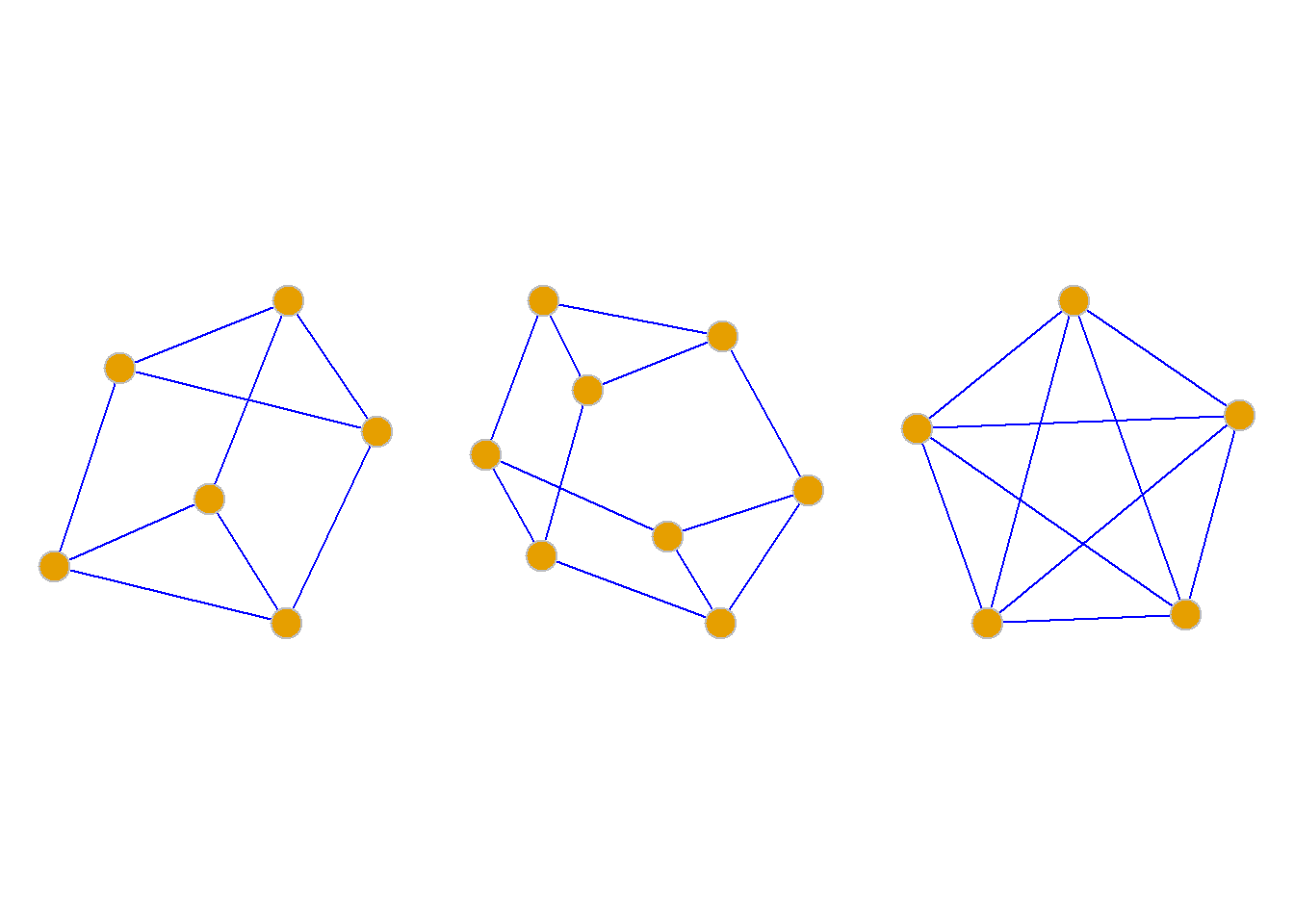
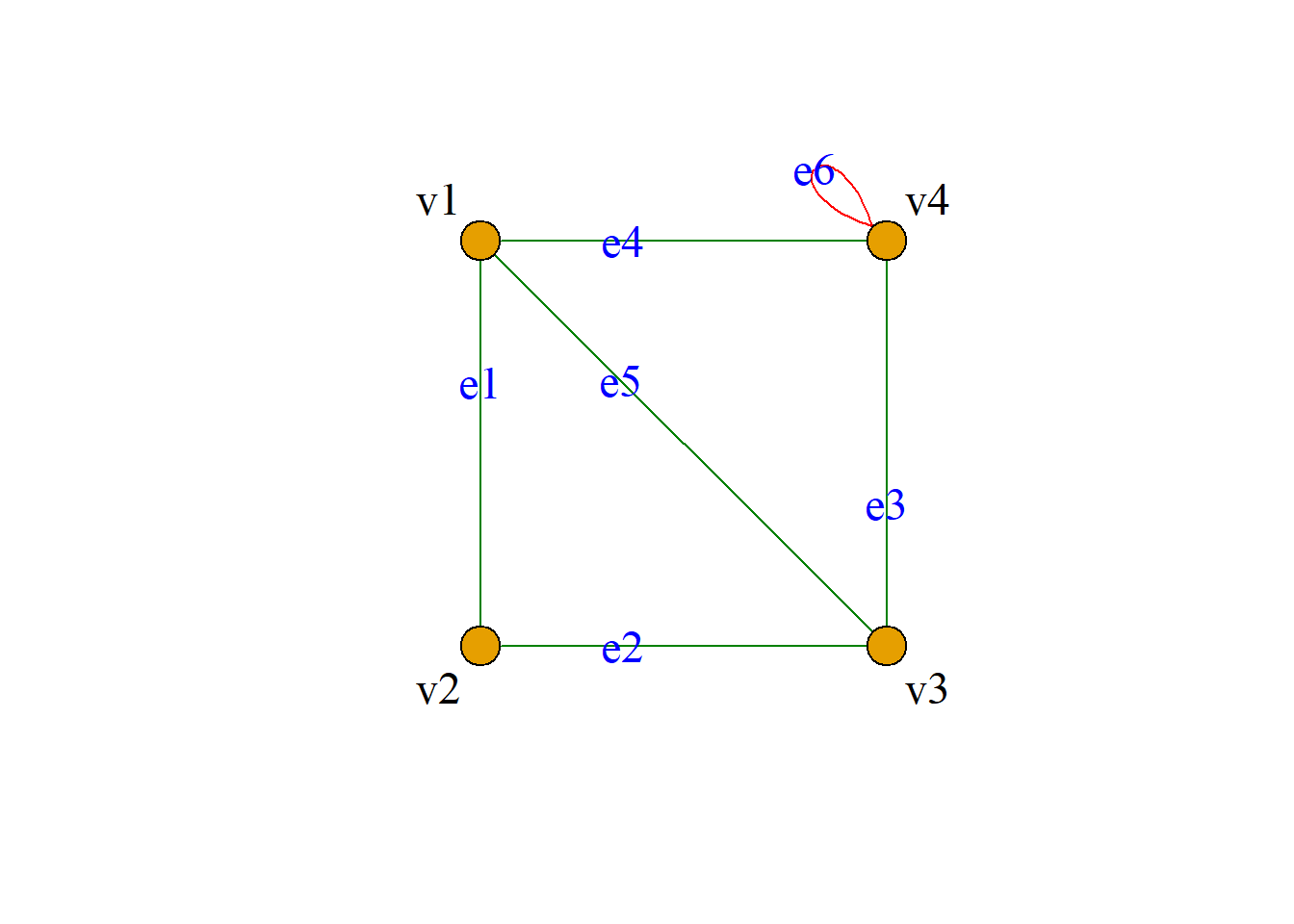
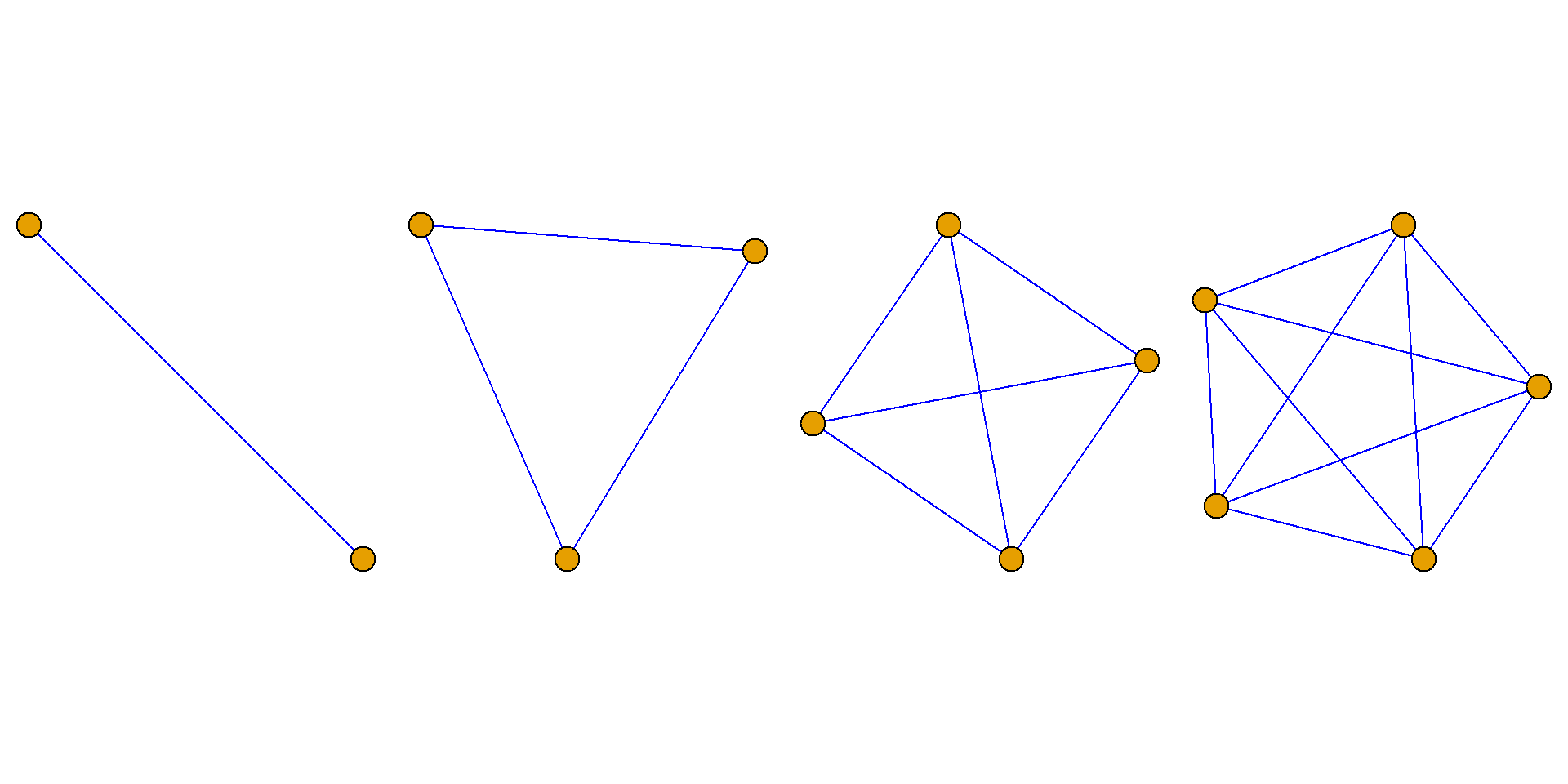
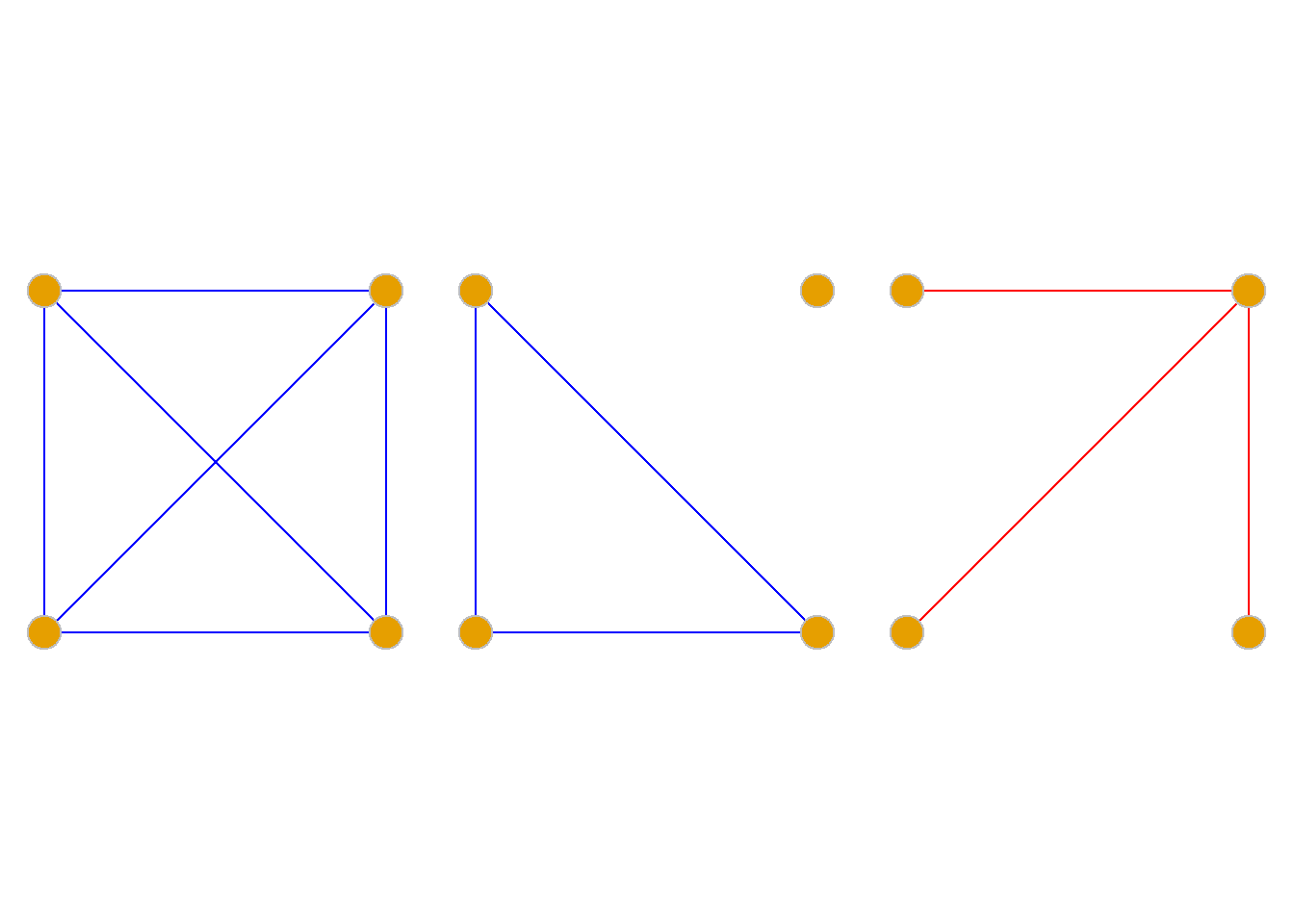
伪图、多重图和简单图

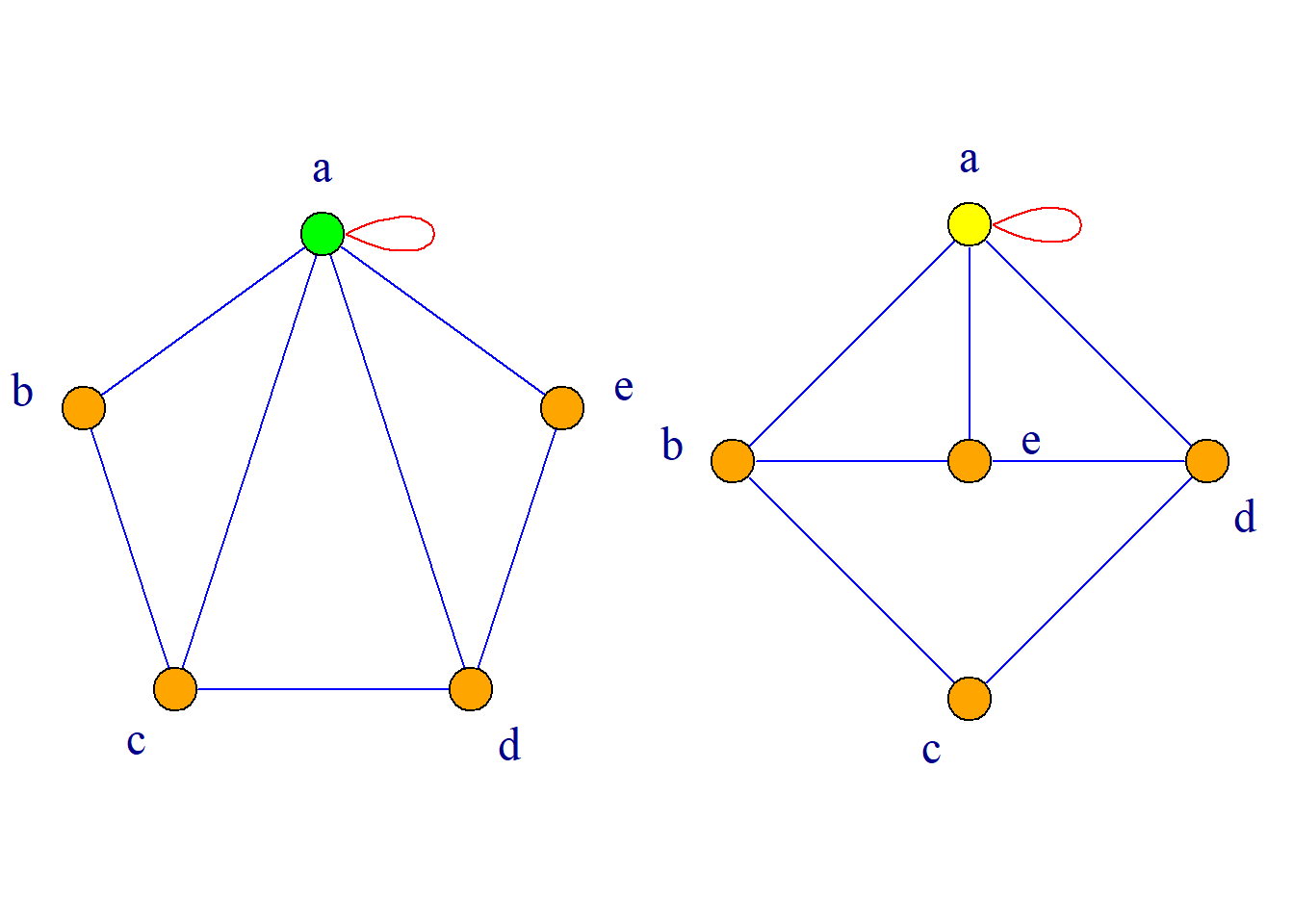
定义: 含有环的图称为伪图.

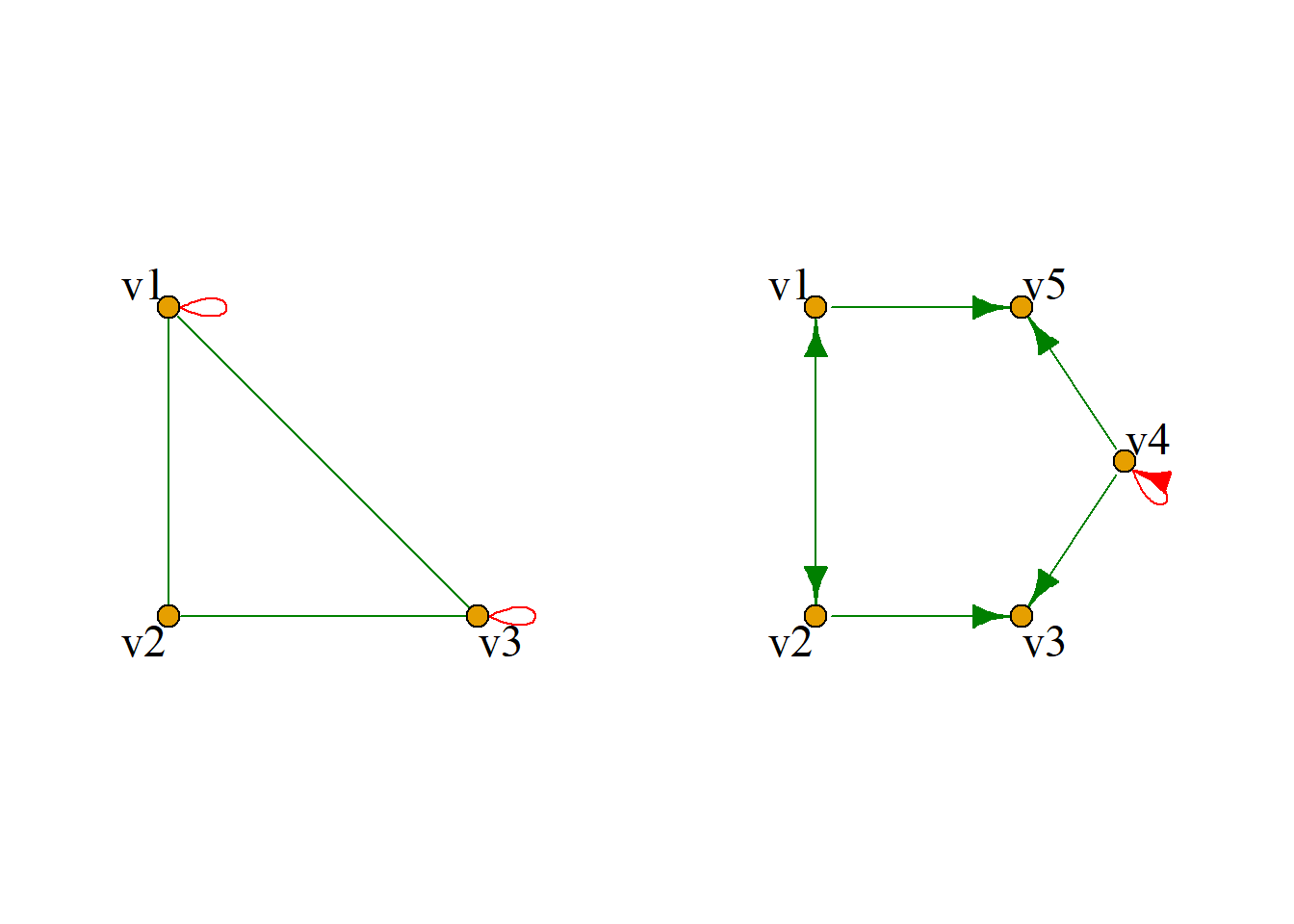
定义: 在图中, 关联同一对结点的边若有多条(对有向图, 这些边的始点和终点应相同), 称这些边为平行边或重边, 平行边的条数称为平行边的重数.

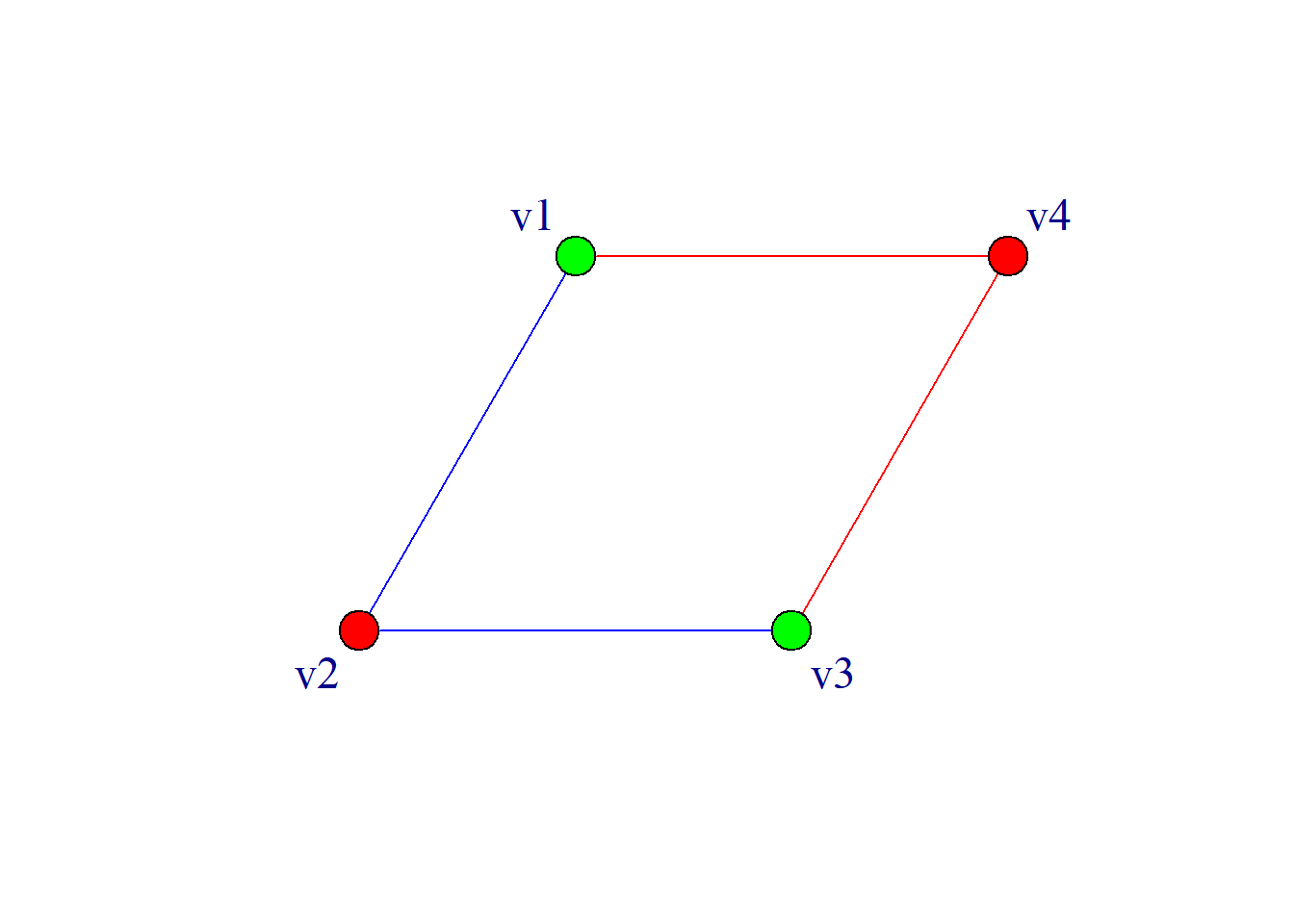
含有平行边但不含有环的图称为多重图.

右图皆为多重图.

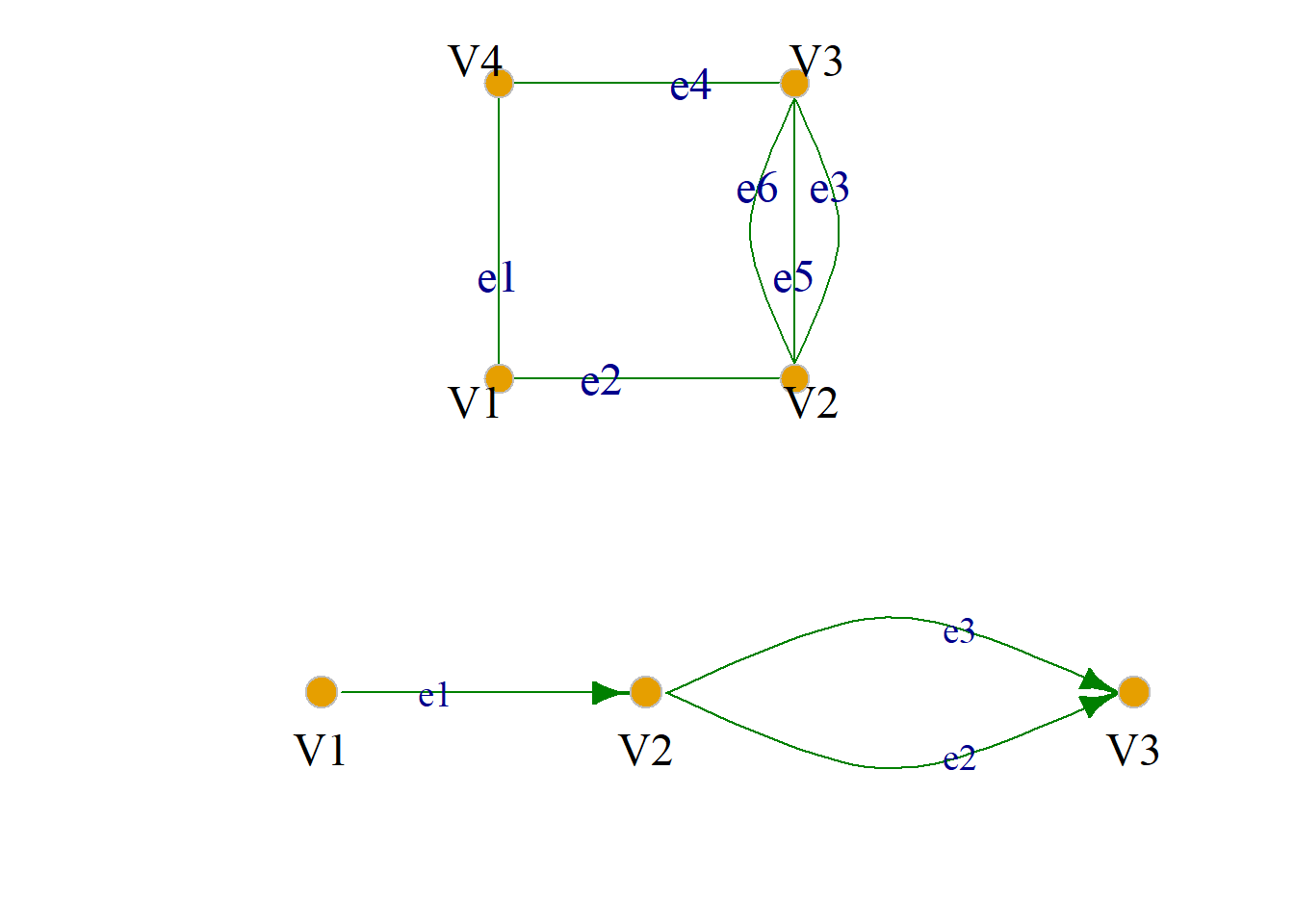
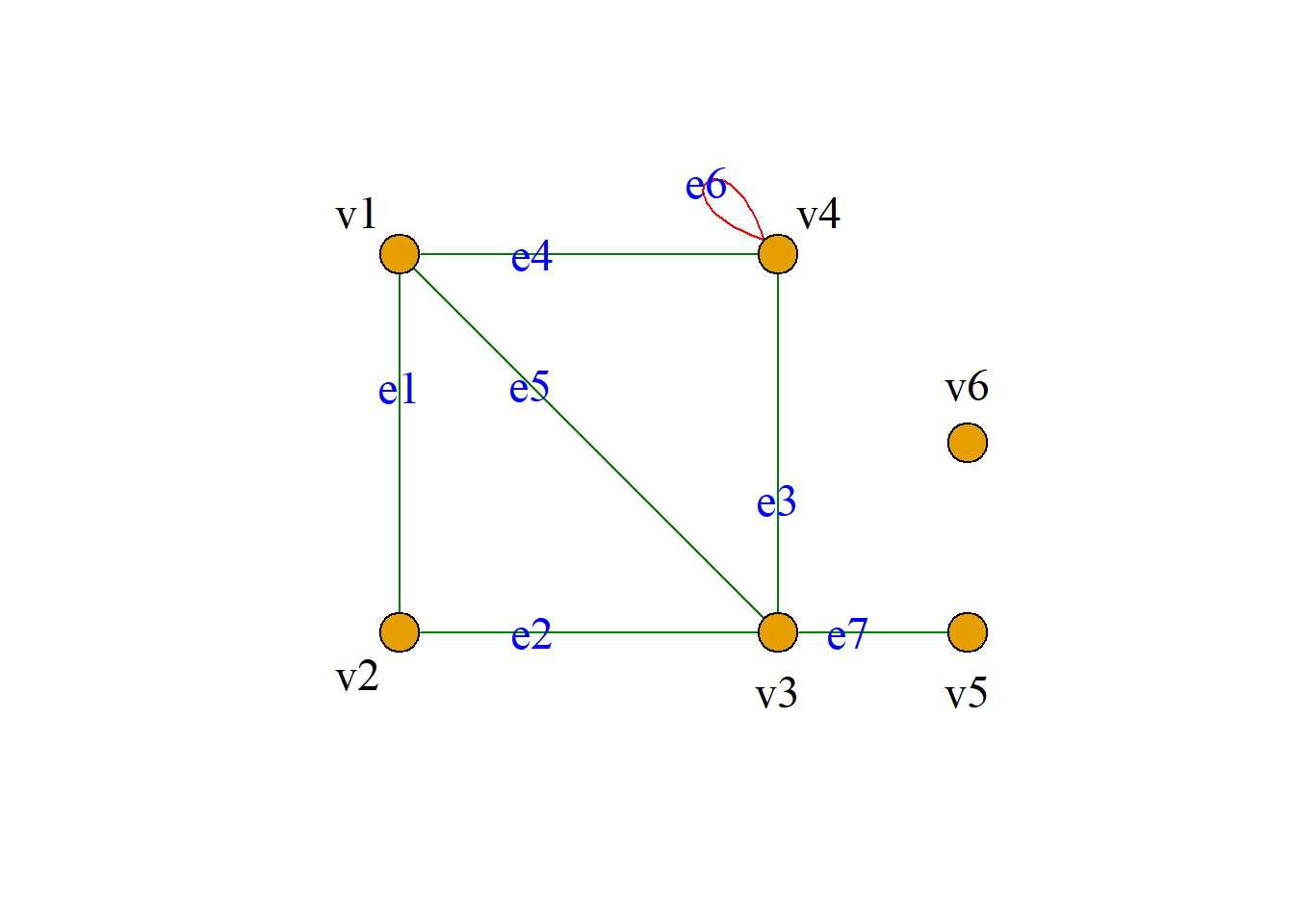
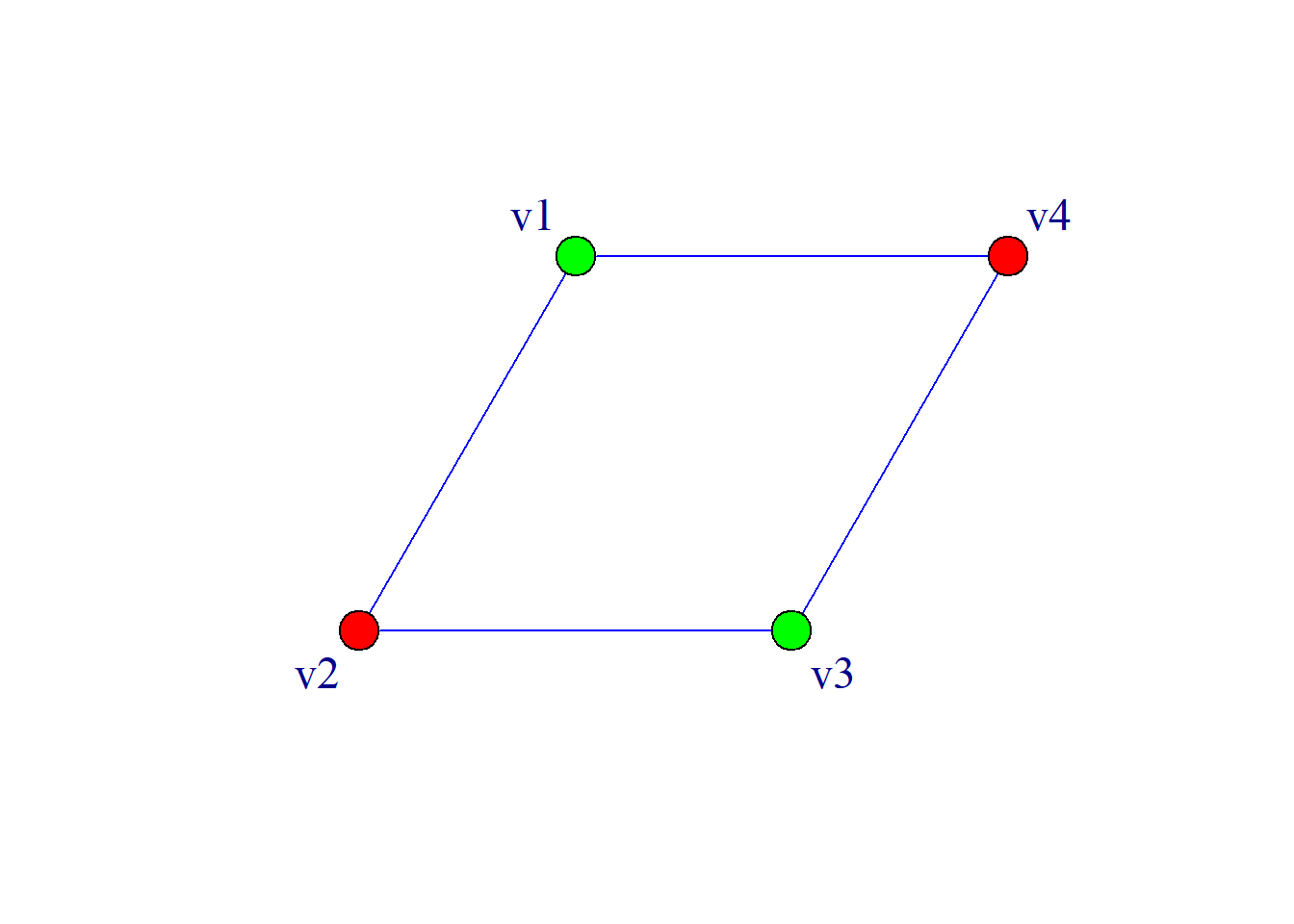
定义: 既不包含平行边又不包含环的图称为简单图.

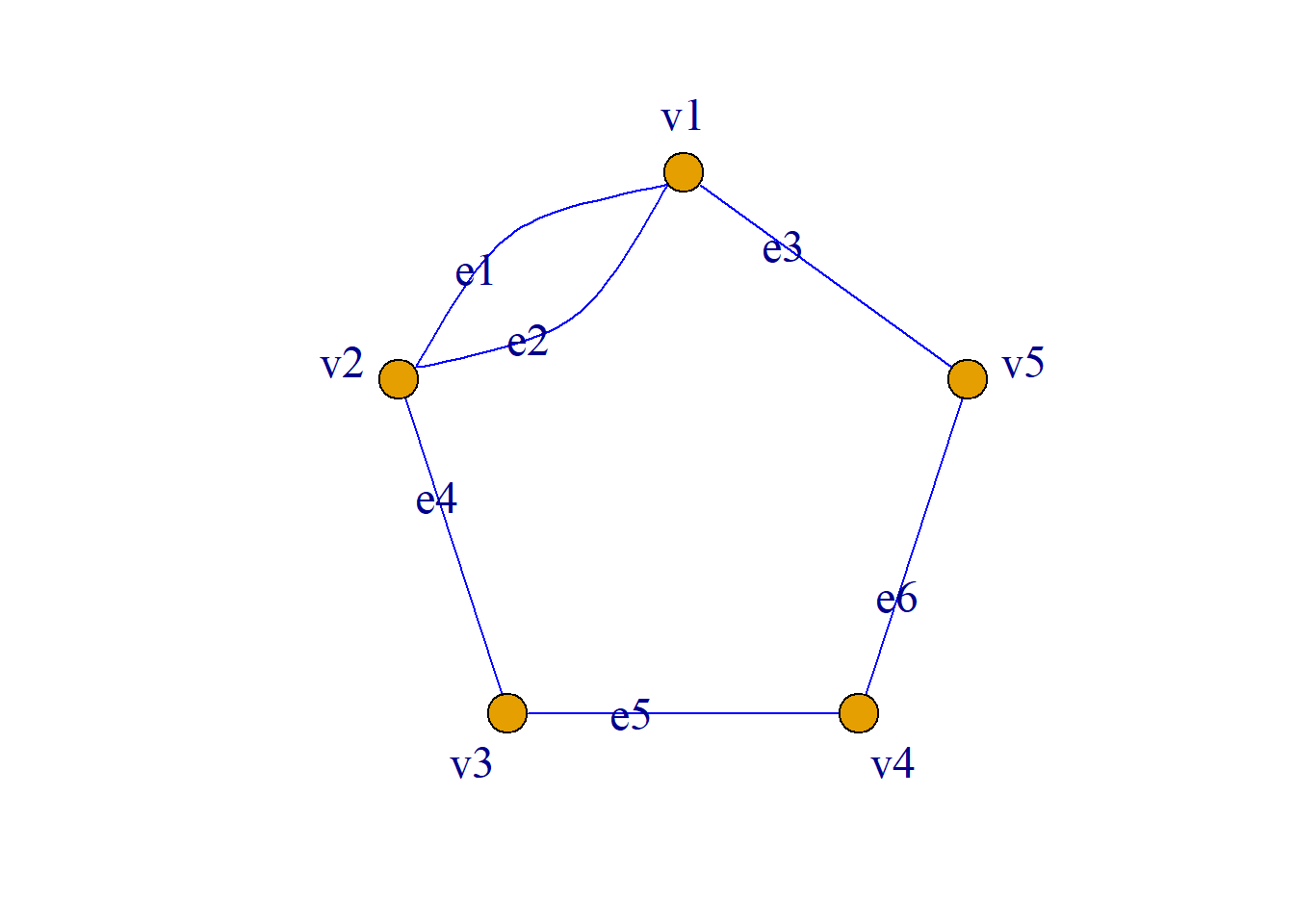
如图所示皆为简单图.

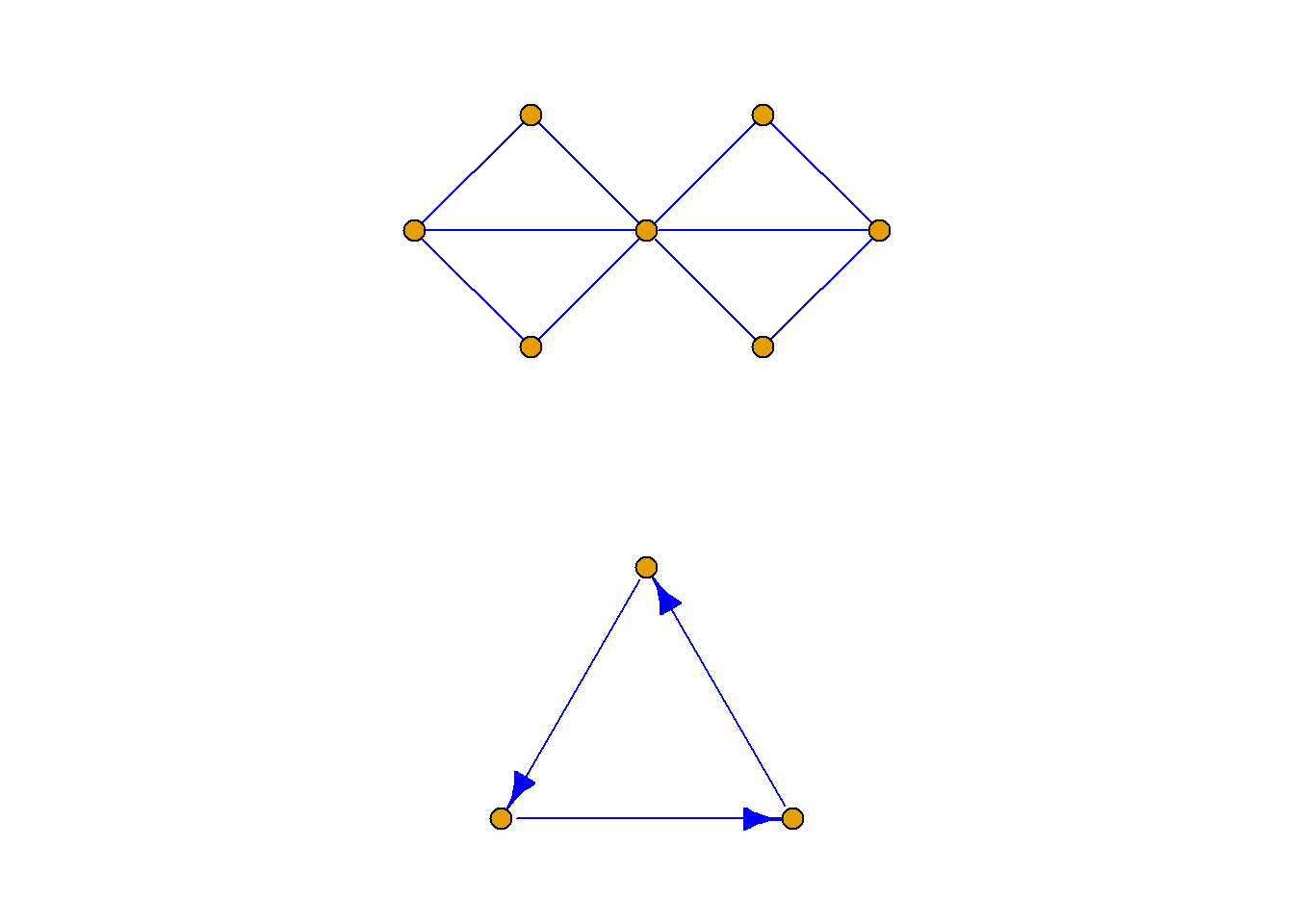
定义: 如果有向图是简单图, 称其为有向简单图 (简单有向图).

如果无向图是简单图, 称其为无向简单图 (简单无向图).

既含有有向边, 又含有无向边的图称为混和图.

完全图

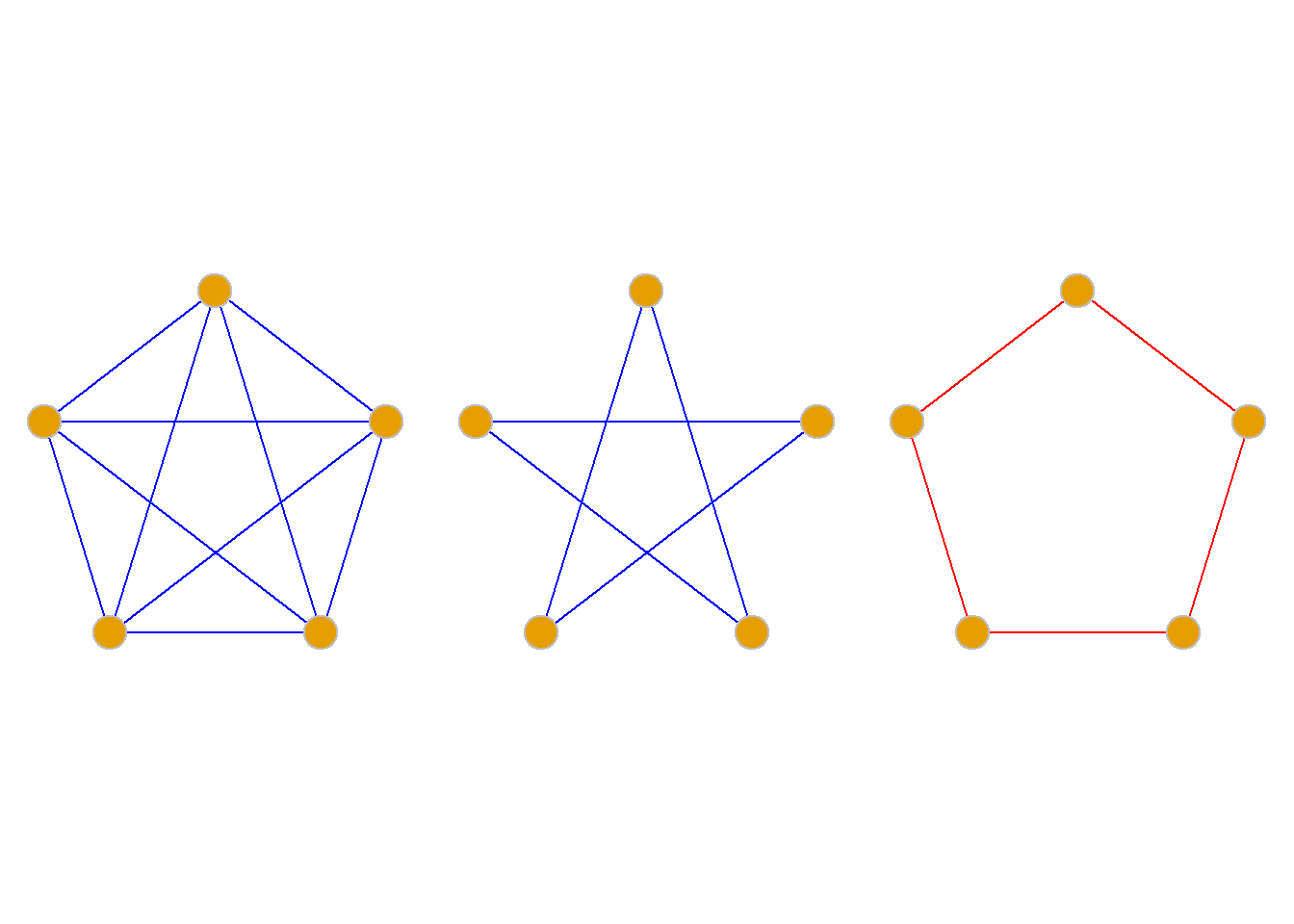
定义: 如果在无向简单图的每对结点之间都恰有一条无向边, 则称该图为无向完全图. 含有\(n\)个结点的无向完全图记为\(K_n\).

定义: 如果在有向简单图的每对结点之间都恰有一对方向相反的有向边, 则称该图为有向完全图. 含有\(n\)个结点的有向完全图记为\(K_n\).

定理: 对于含有\(n\)个结点\(m\)条边的无向完全图\(K_n\), 有 \[m=\frac{n(n-1)}{2}\] 证明: 在无向完全图\(K_n\)中, 任意两结点间都有一条边相连接, \(n\)个结点中任取两个的组合数为: \[C_n^2=\frac{1}{2}n(n-1)\]

故\(K_n\)的边数为: \[m=\frac{n(n-1)}{2}\]

定理: 对于含有\(n\)个结点\(m\)条边的有向完全图\(K_n\), 有\(m=n(n-1)\).

子图

定义: 设\(G={\langle}V, E{\rangle}\)和\(G^\prime={\langle}V^\prime, E^\prime{\rangle}\)是两个图, 于是

如果\(V^\prime{\subseteq}V\)且\(E^\prime{\subseteq}E\), 则称\(G^\prime\)是\(G\)的子图, 记为\(G^\prime{\subseteq}G\).
如果\(V^\prime{\subseteq}V\)且\(E^\prime{\subseteq}E\), 但\(E^\prime{\neq}E\)或\(V^\prime{\neq}V\), 则称\(G^\prime\)是\(G\)的真子图, 记为\(G^\prime{\subset}G\).
如果\(V^\prime=V\)且\(E^\prime{\subseteq}E\), 则称\(G^\prime\)是\(G\)的生成子图或支撑子图. 图\(G\)本身和零图称为其平凡生成子图.

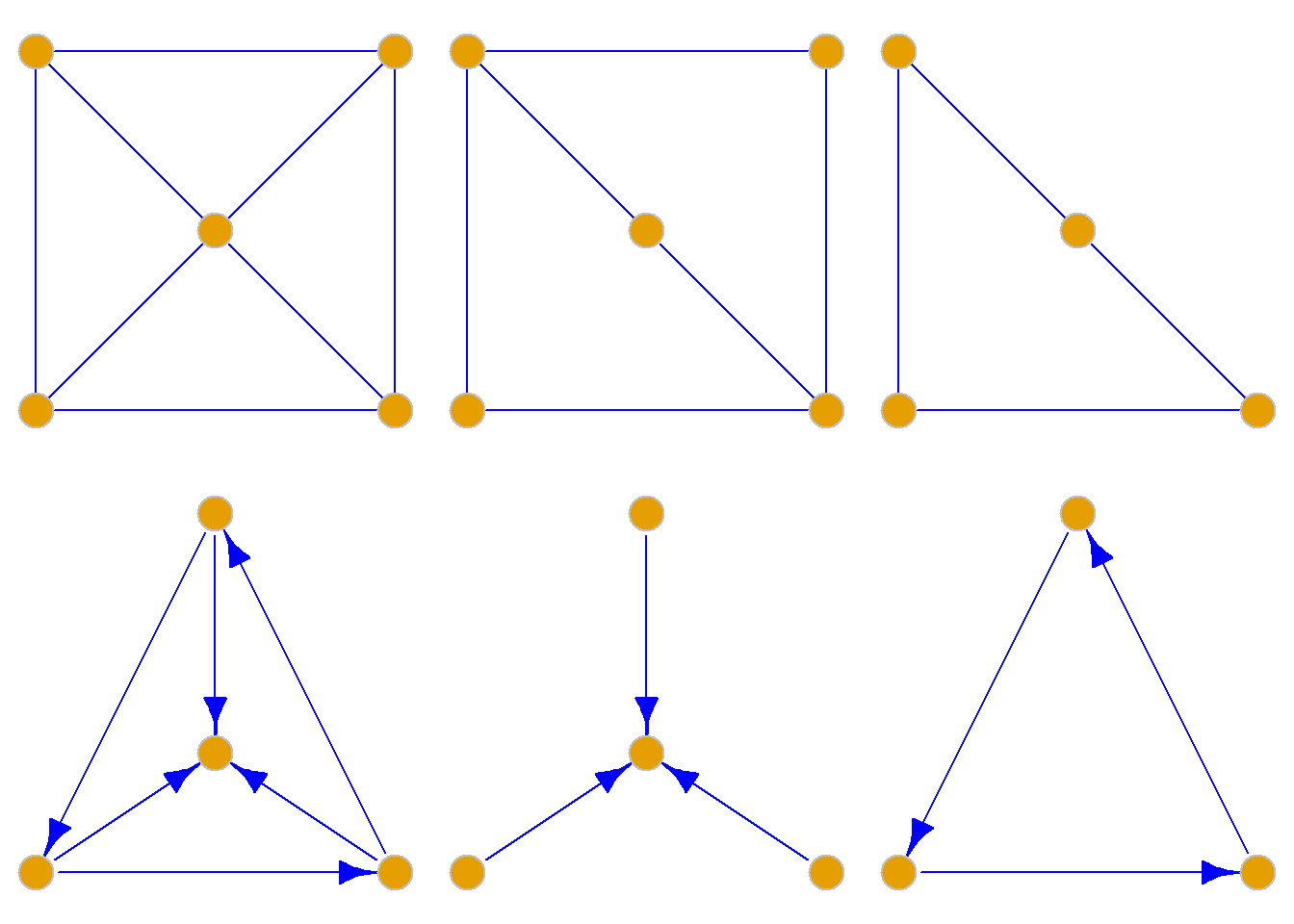
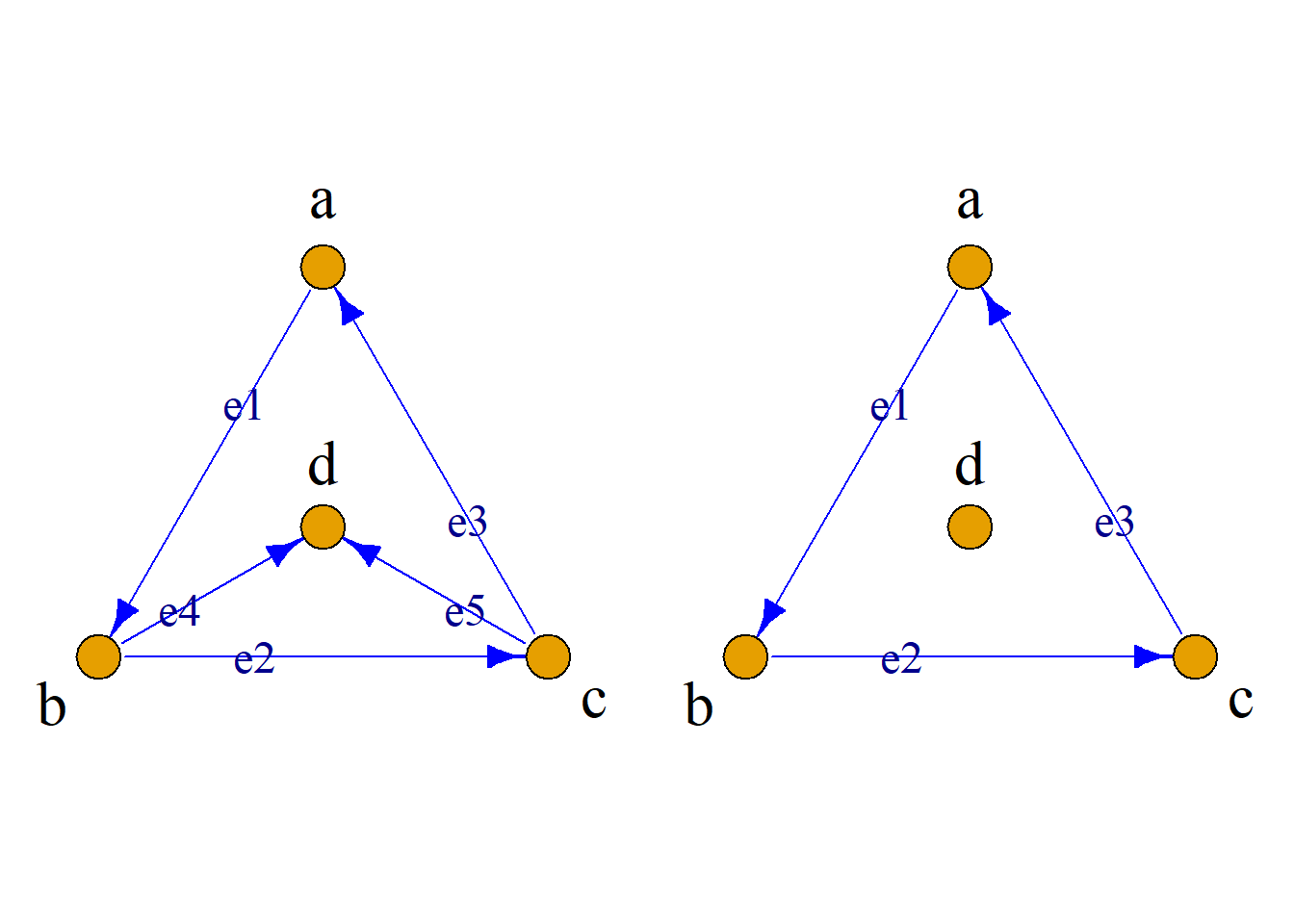
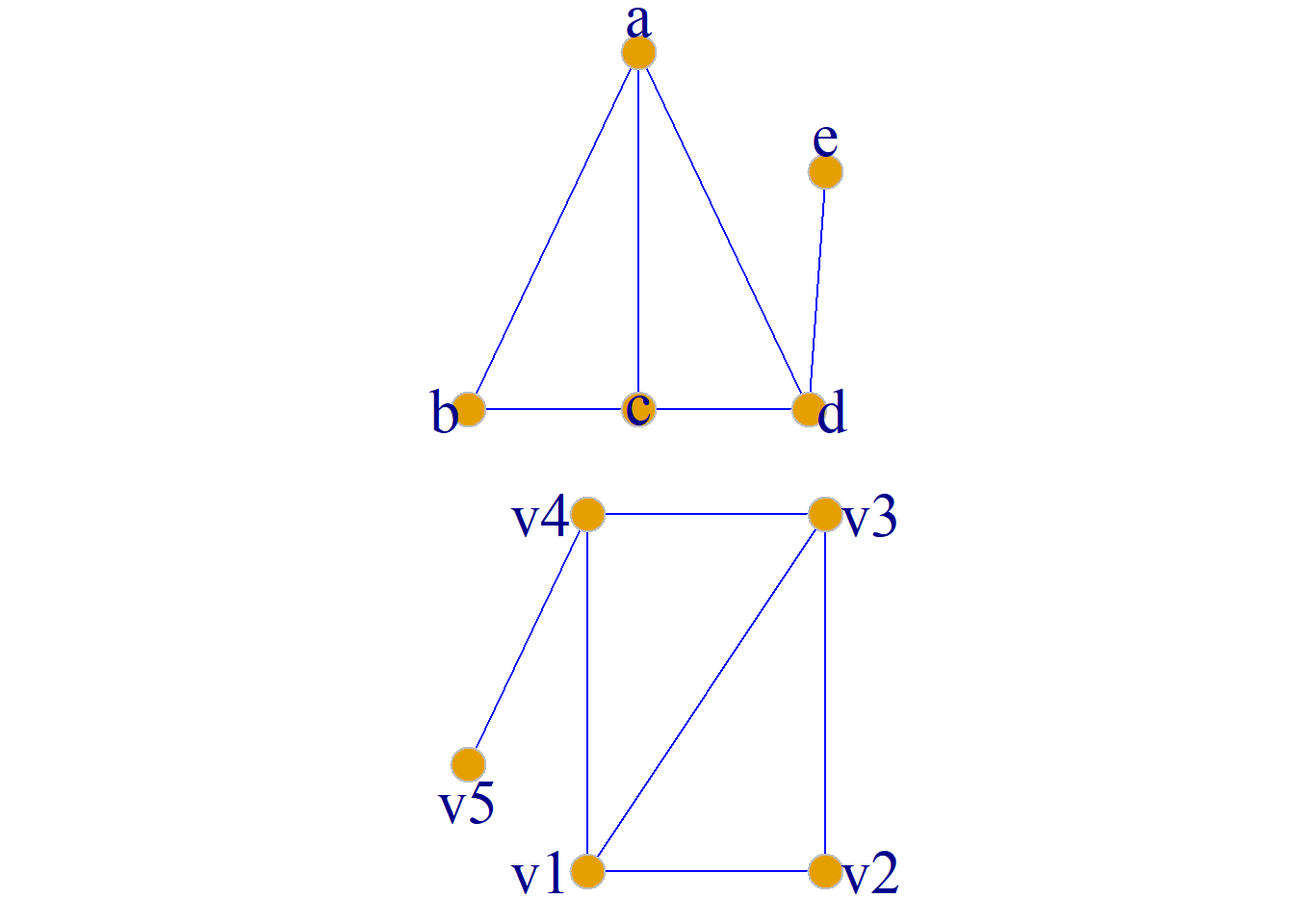
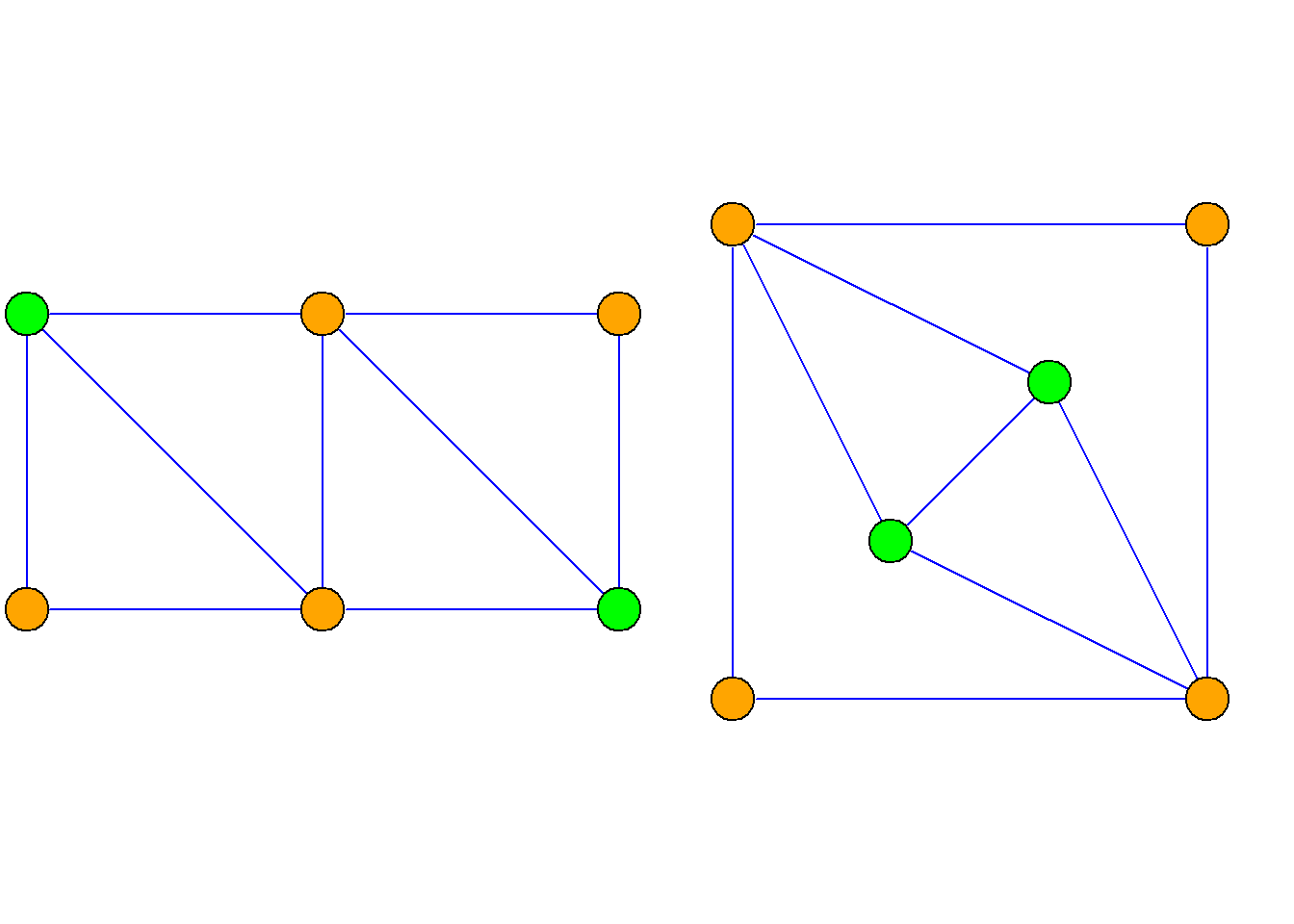
(b)(c)均是(a)的子图和真子图, (b)也是(a)的生成子图; (e)(f)是(d)的子图和真子图, (e)也是(d)的生成子图.

定义: 对图\(G={\langle}V, E{\rangle}\), \(V^\prime{\subseteq}V\)非空子集, 以\(V^\prime\)为结点集, 以两端点均在\(V^\prime\)中的边的全体为边集构成的图, 称为由结点集\(V^\prime\)导出的\(G\)的子图, 简称导出子图, 记为\(G[V^\prime]\).

例: 如图所示, 选择子集\(V^\prime=\{a, b, c\}\)

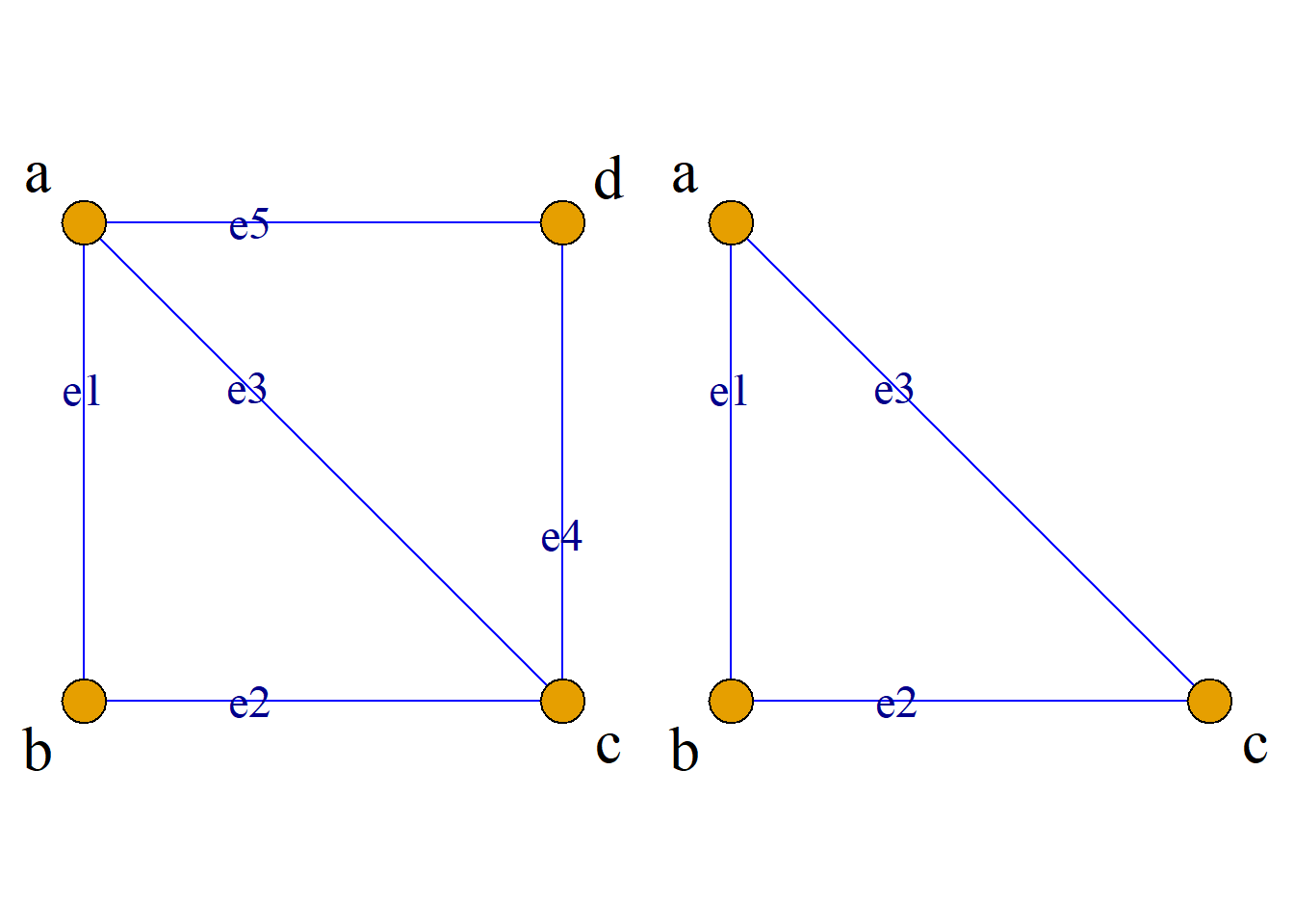
定义: 对于图\(G={\langle}V, E{\rangle}\), 设\(E^\prime\)是\(E\)的非空子集, 以\(E^\prime\)为边集, 以\(E^\prime\)中边的端点的全体为结点集构成的图, 称为由边集\(E^\prime\)导出的\(G\)的子图, 简称导出子图, 记为\(G[E^\prime]\).

例: 如图所示, 选择子集\(E^\prime=\{e_1, e_2, e_3\}\)

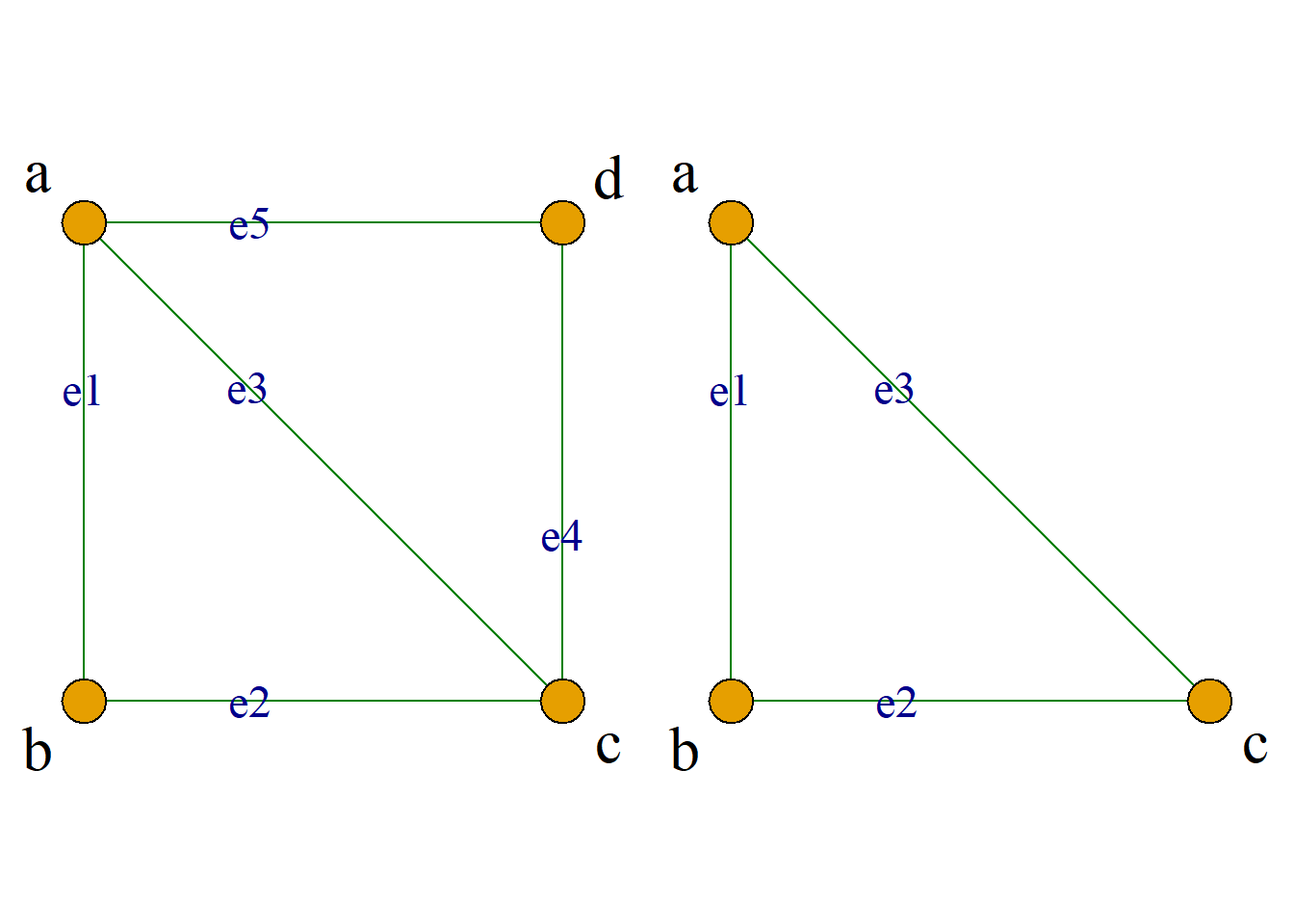
几类导出子图的表示:

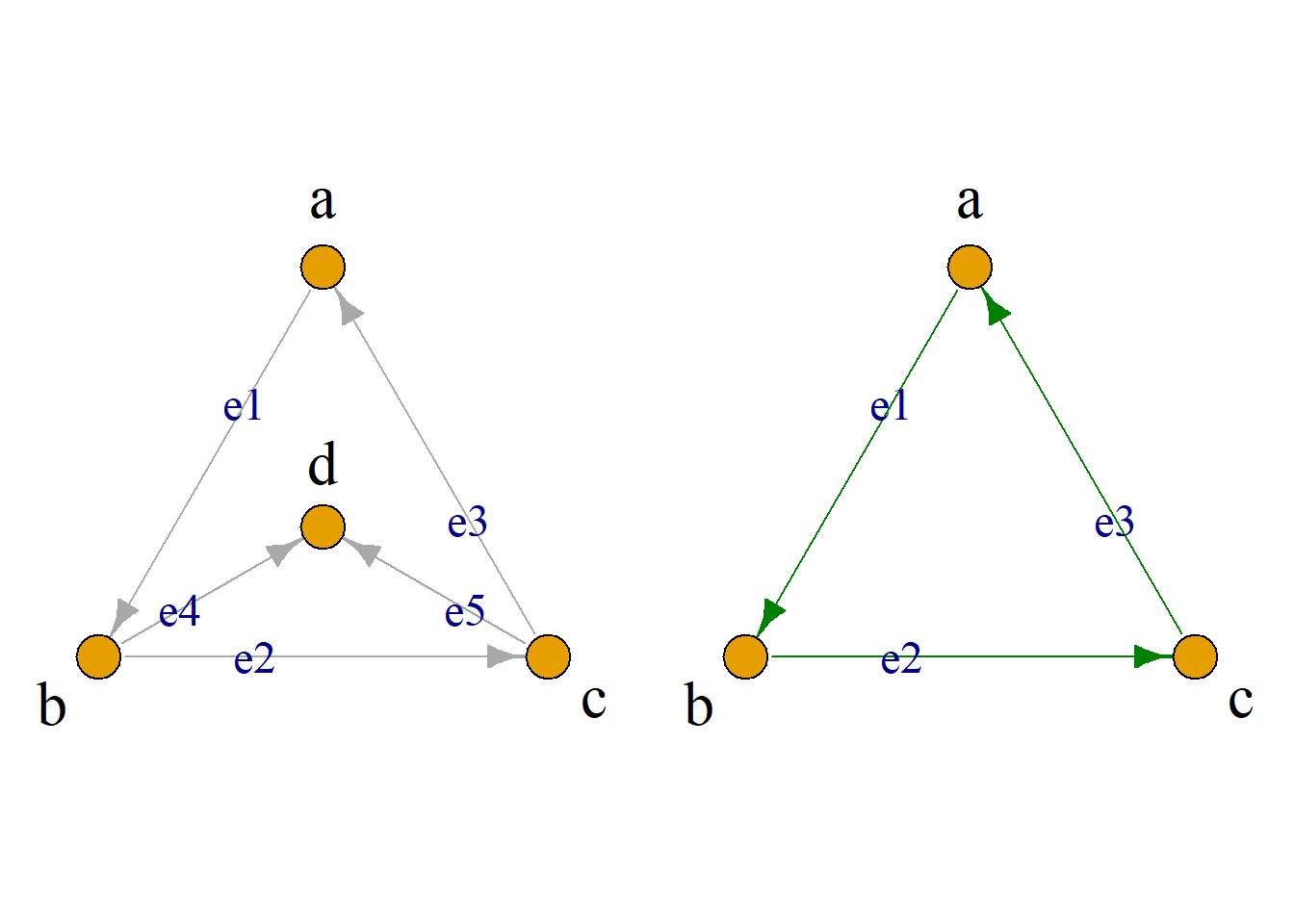
对于图\(G={\langle}V, E{\rangle}\), \(V^\prime{\subseteq}V\), 从\(G\)中删除\(V^\prime\)中各结点及关联各结点的边, 所得到的子图记为\(G-V^\prime\), 它实际上就是导出子图\(G[V-V^\prime]\).

特别地若\(V^\prime=\{v\}\), 简记为\(G-v\).

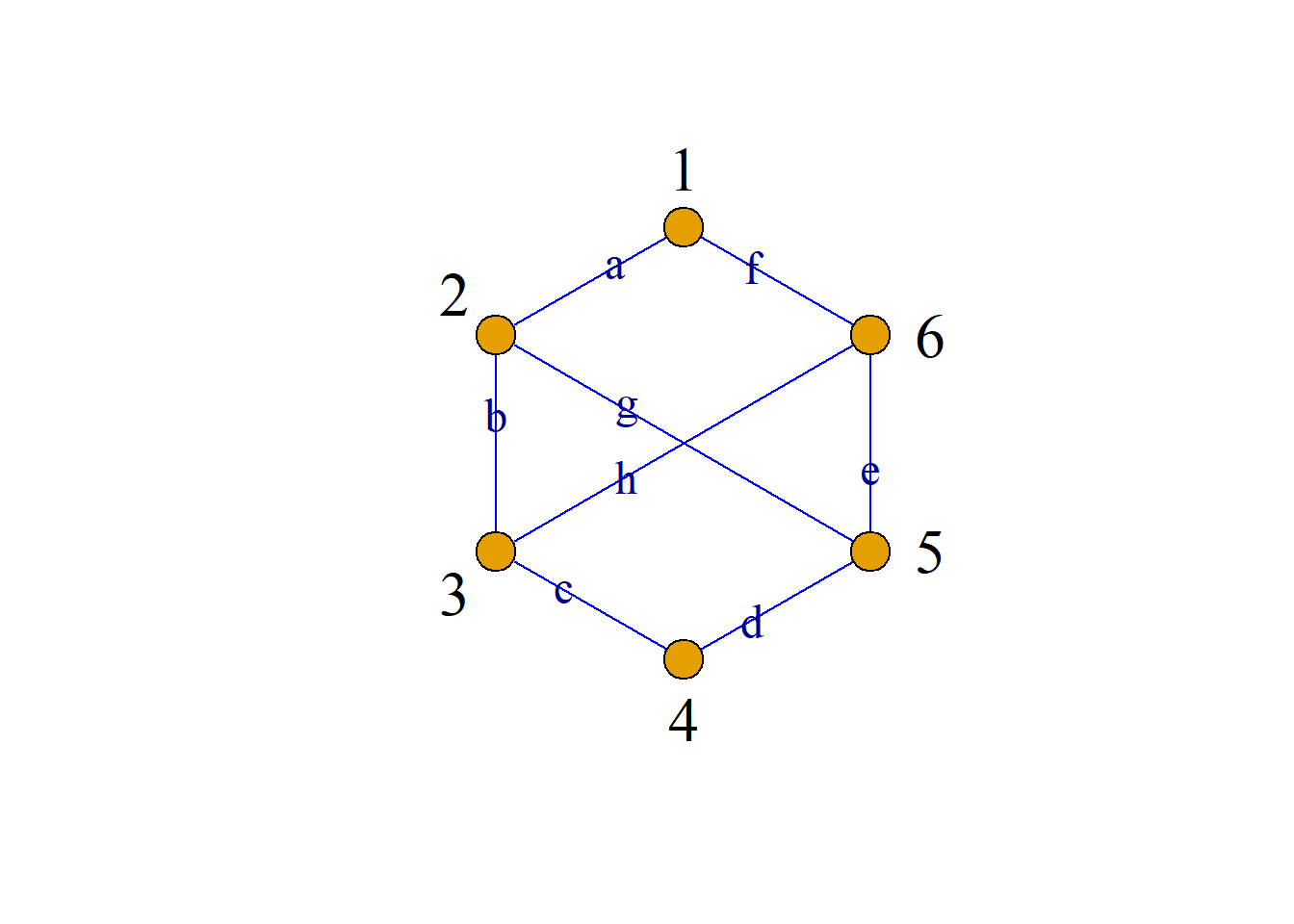
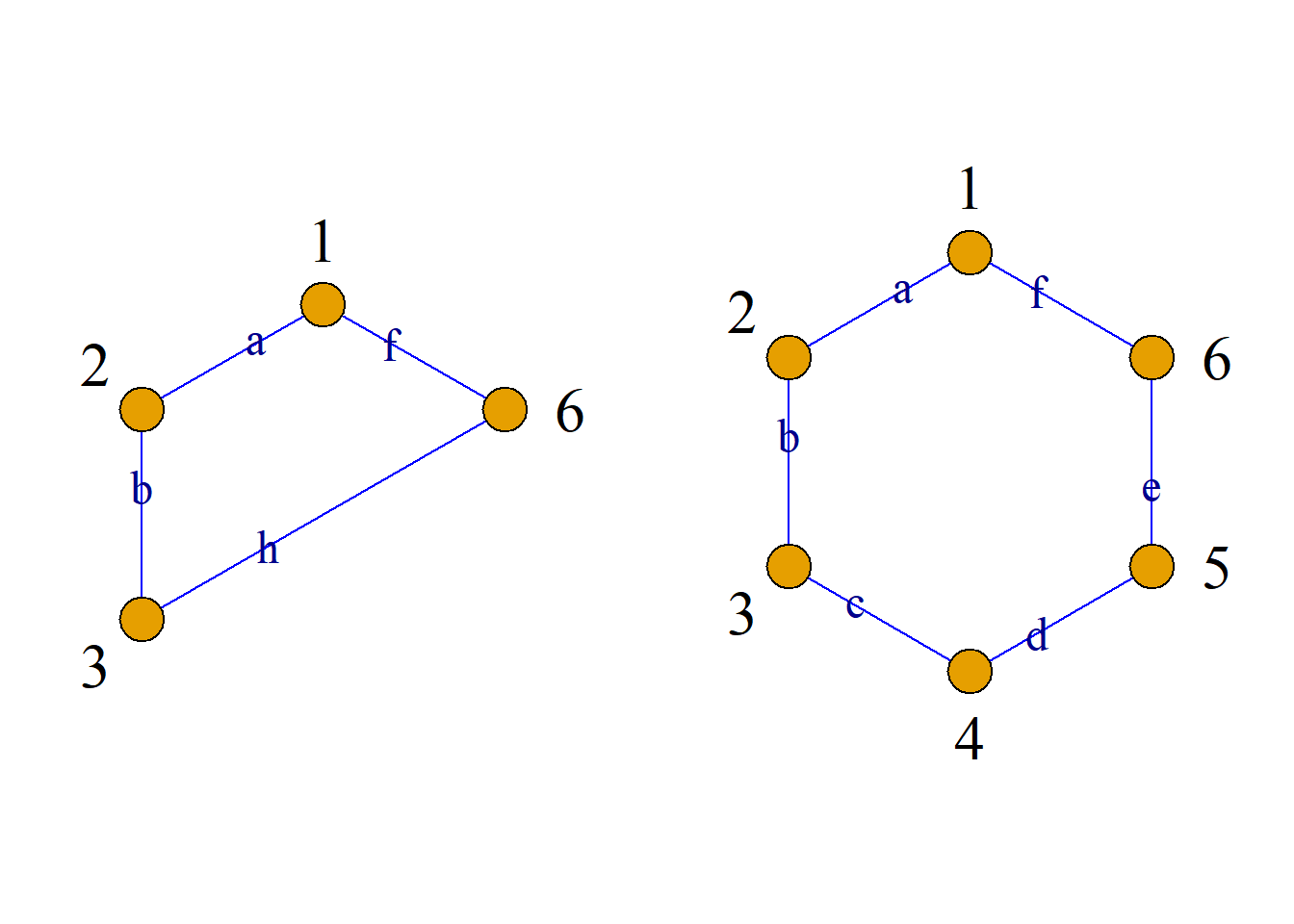
例: \(G-\{d, e\}\).

对于图\(G={\langle}V, E{\rangle}\), \(E^\prime{\subseteq}E\), 从\(G\)中删除\(E^\prime\)中各边, 所得到的\(G\)的子图记为\(G-E^\prime\), 它实际上是以\(V\)为结点集, \(E-E^\prime\)为边集所生成的\(G\)的生成子图.

特别地, 若\(E^\prime=\{e\}\), 简记为\(G-e\).

补图

定义: 设图\(G^\prime={\langle}V^\prime, E^\prime{\rangle}\)是图\(G={\langle}V, E{\rangle}\)的子图.

给定另一个图\(G^{\prime\prime}={\langle}V^{\prime\prime}, E^{\prime\prime}{\rangle}\), 若有\(E^{\prime\prime}=E-E^\prime\), 而\(V^{\prime\prime}\)是仅包含\(E^{\prime\prime}\)中的边所关联的结点以及\(G\)中存在而\(G^\prime\)没有的孤立点的集合, 则称\(G^{\prime\prime}\)是子图\(G^\prime\)相对于图\(G\)的补图, 记为\(G^{\prime\prime}=G-G^\prime\).

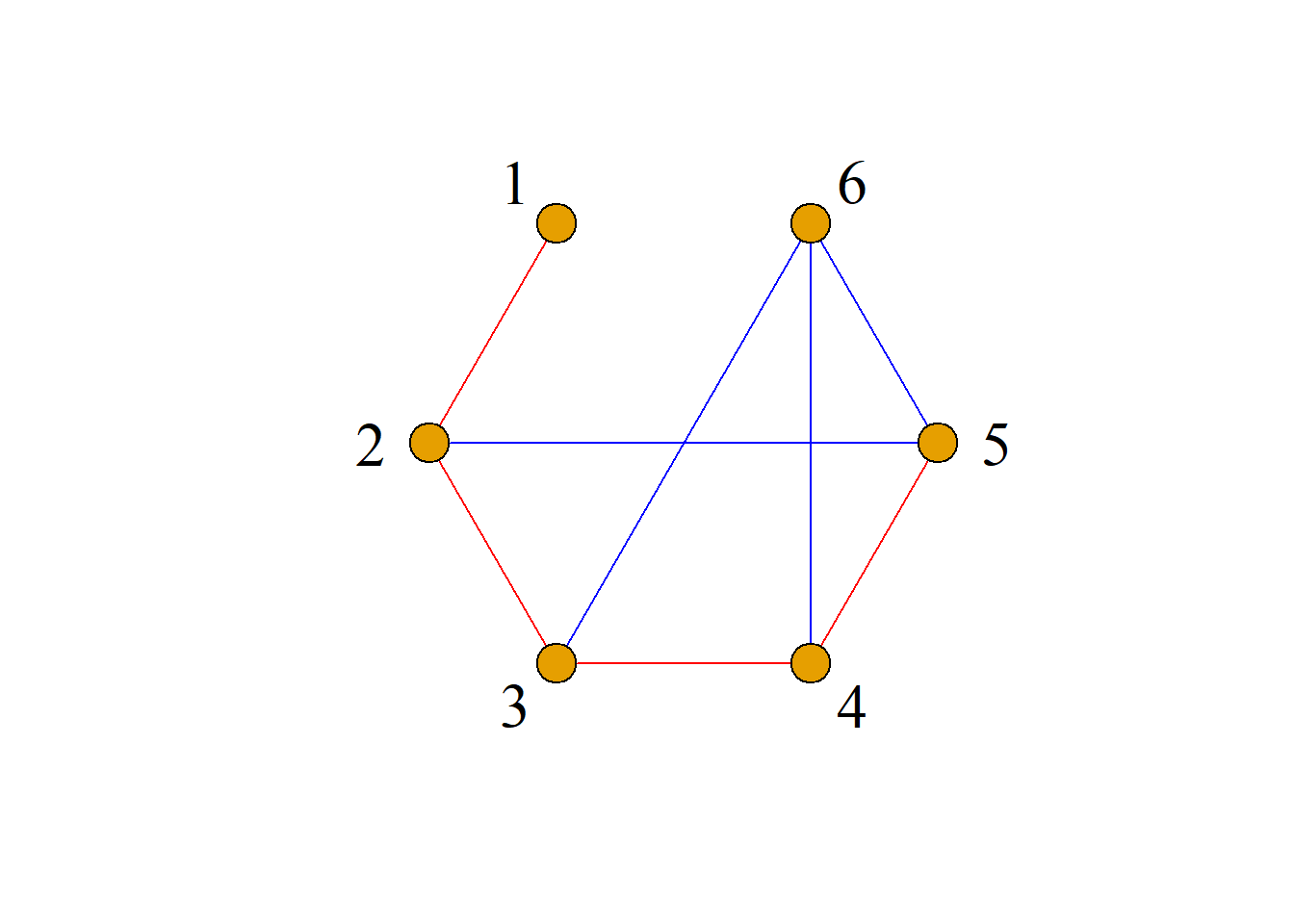
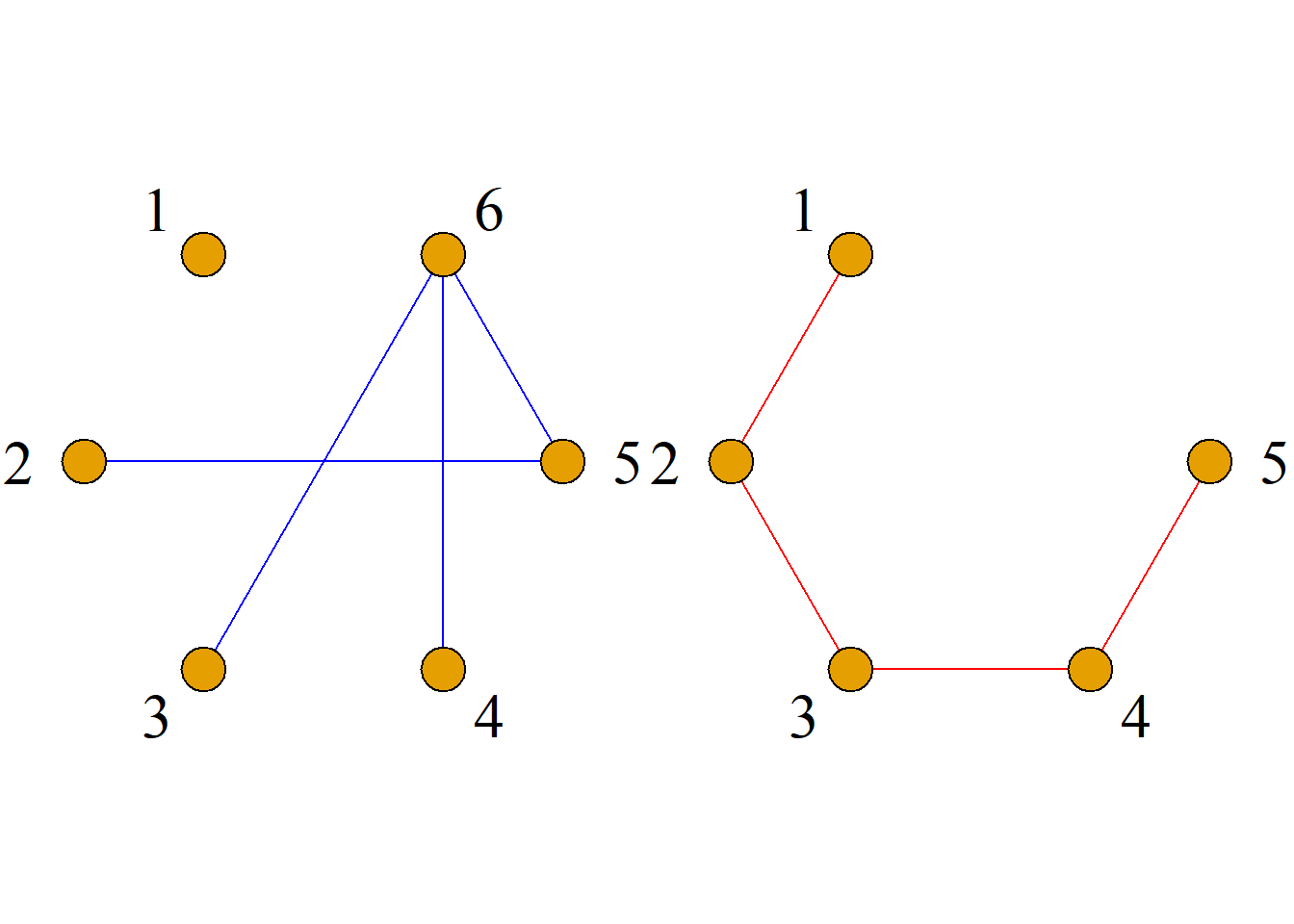
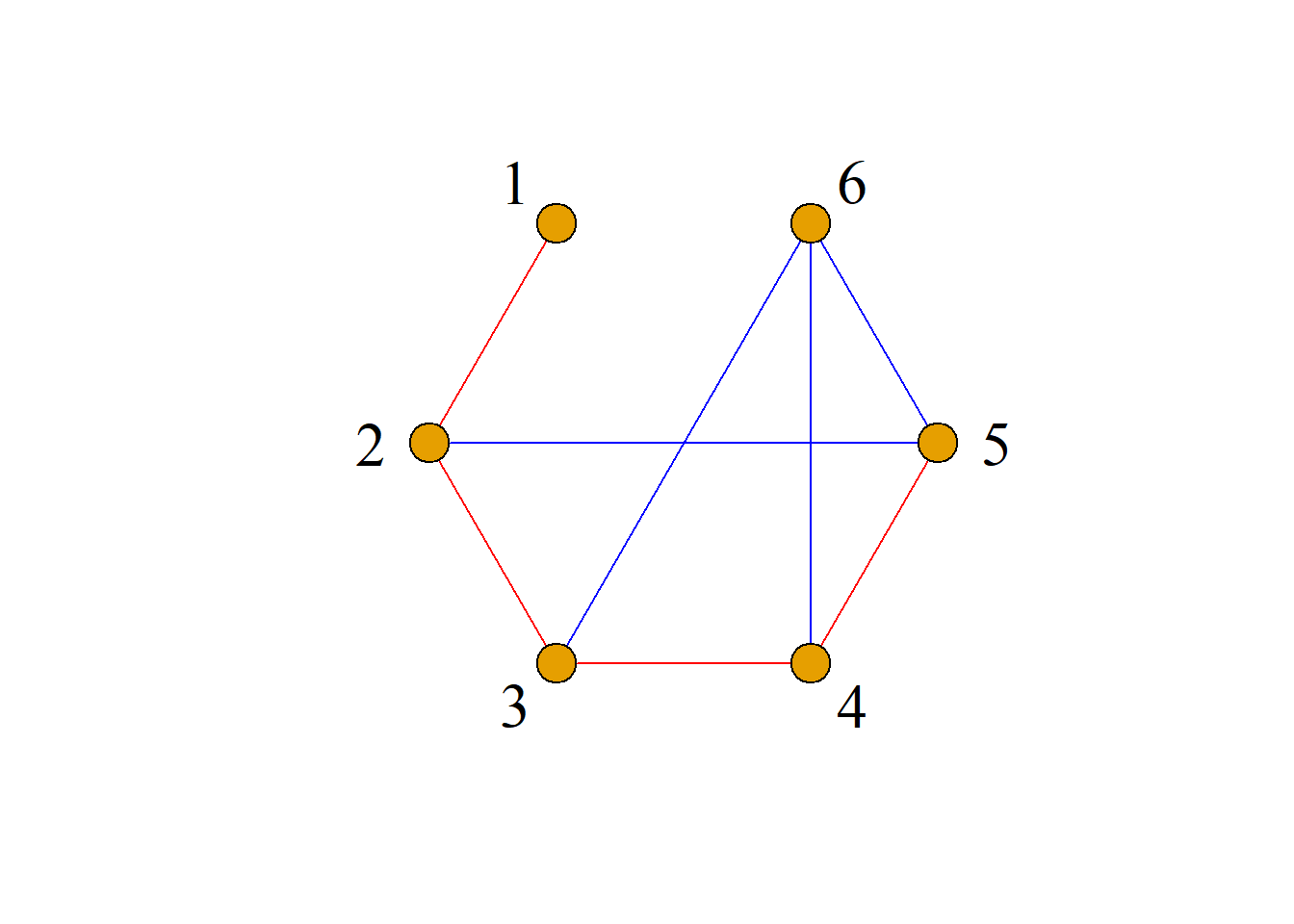
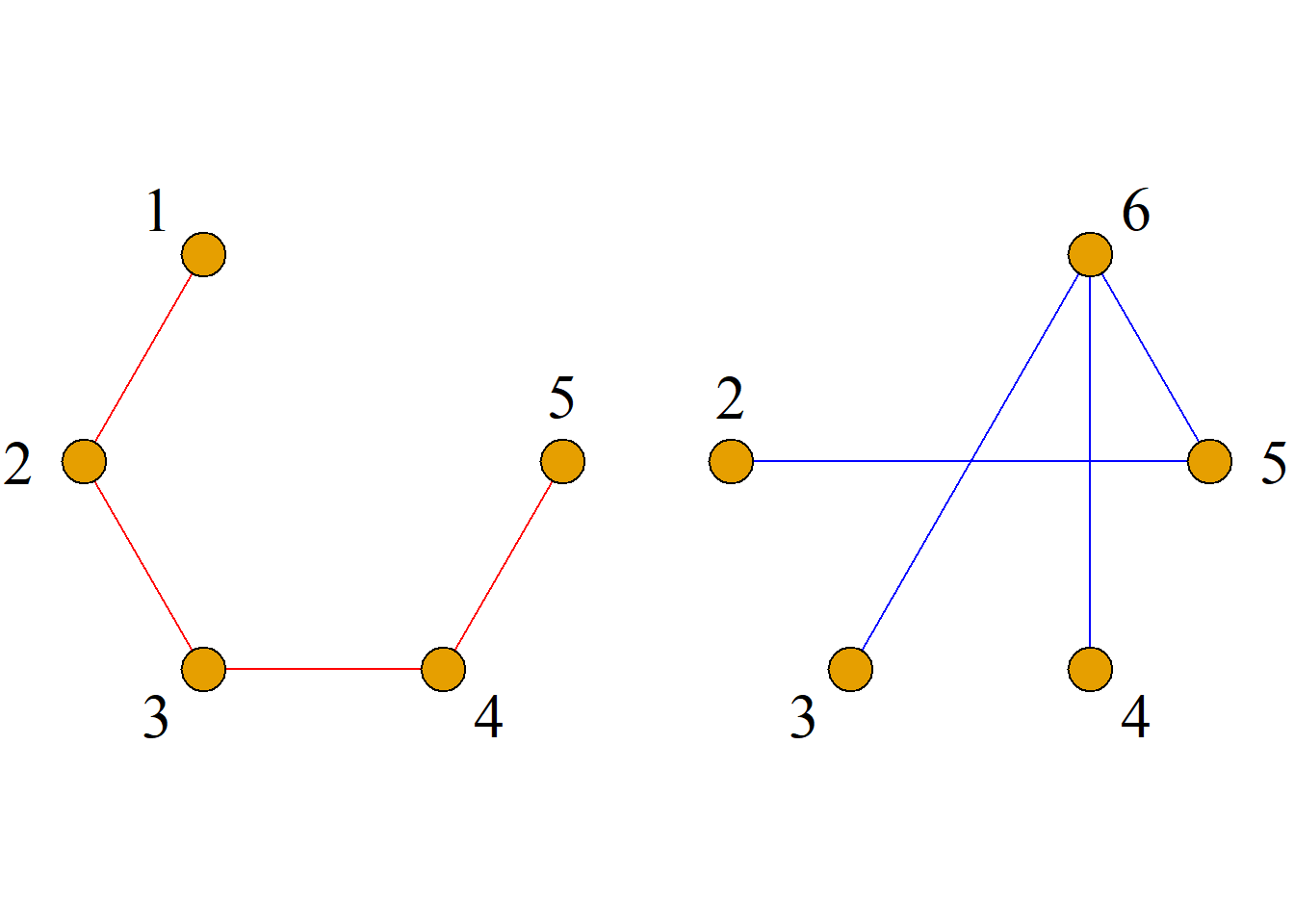
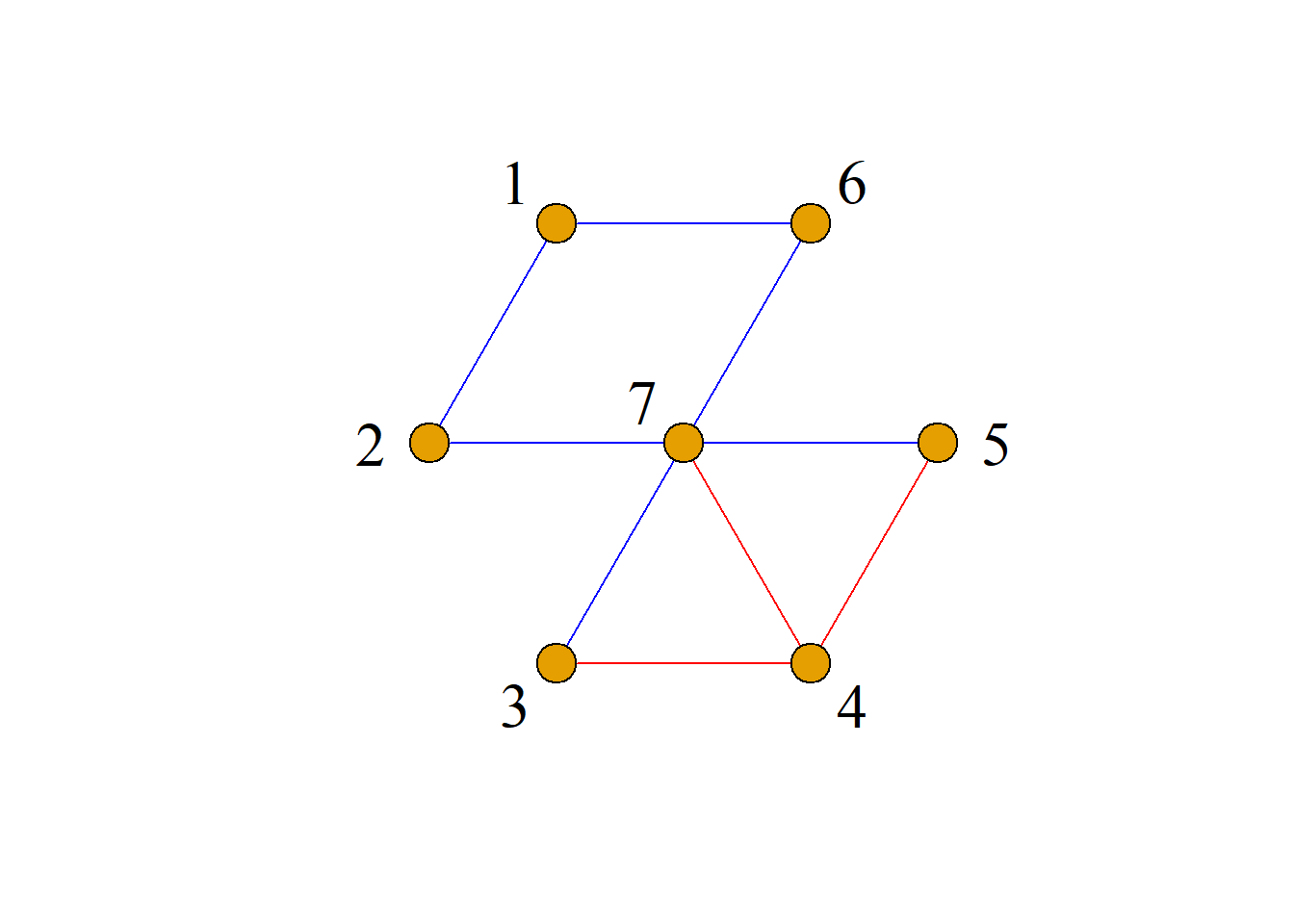
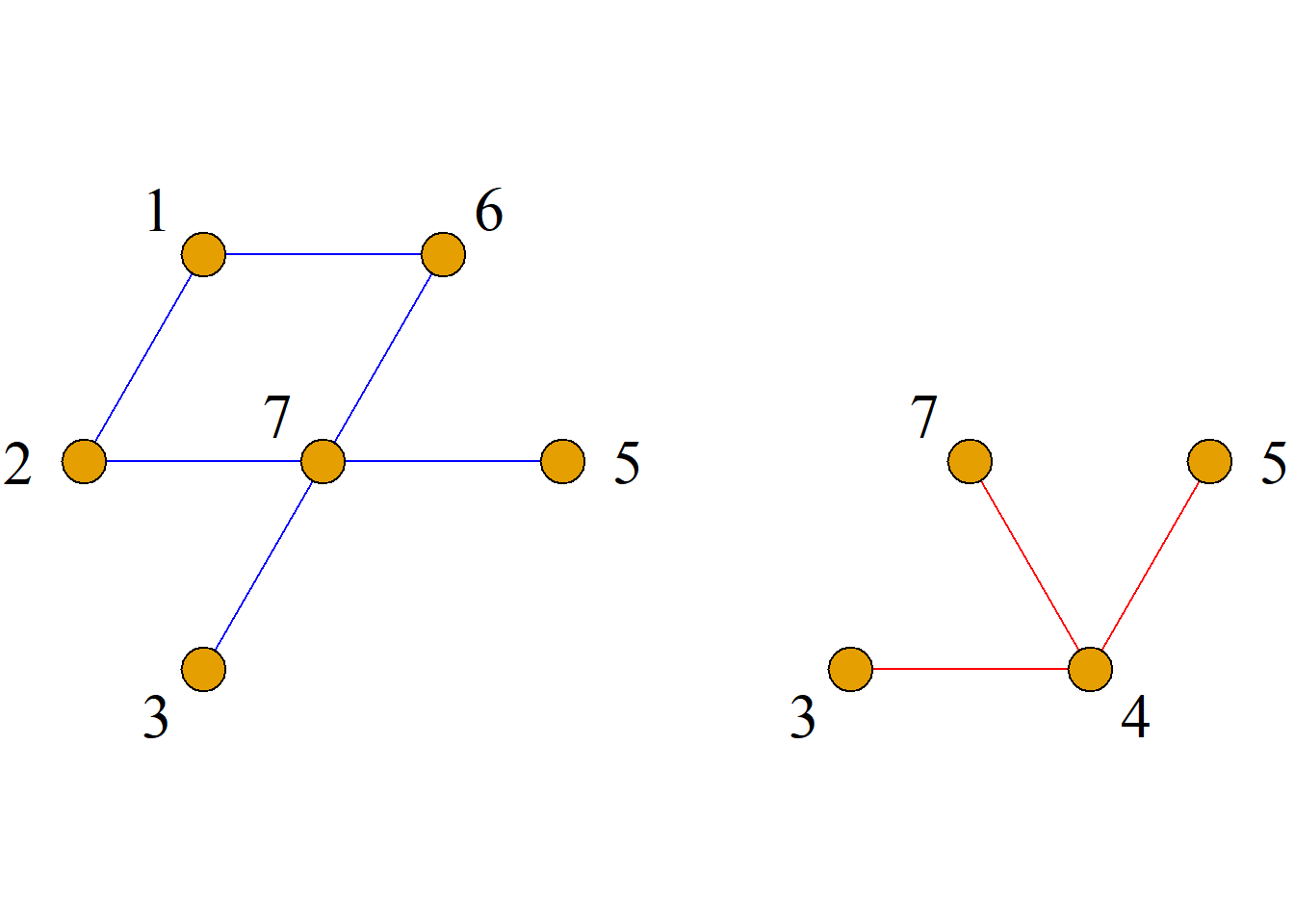
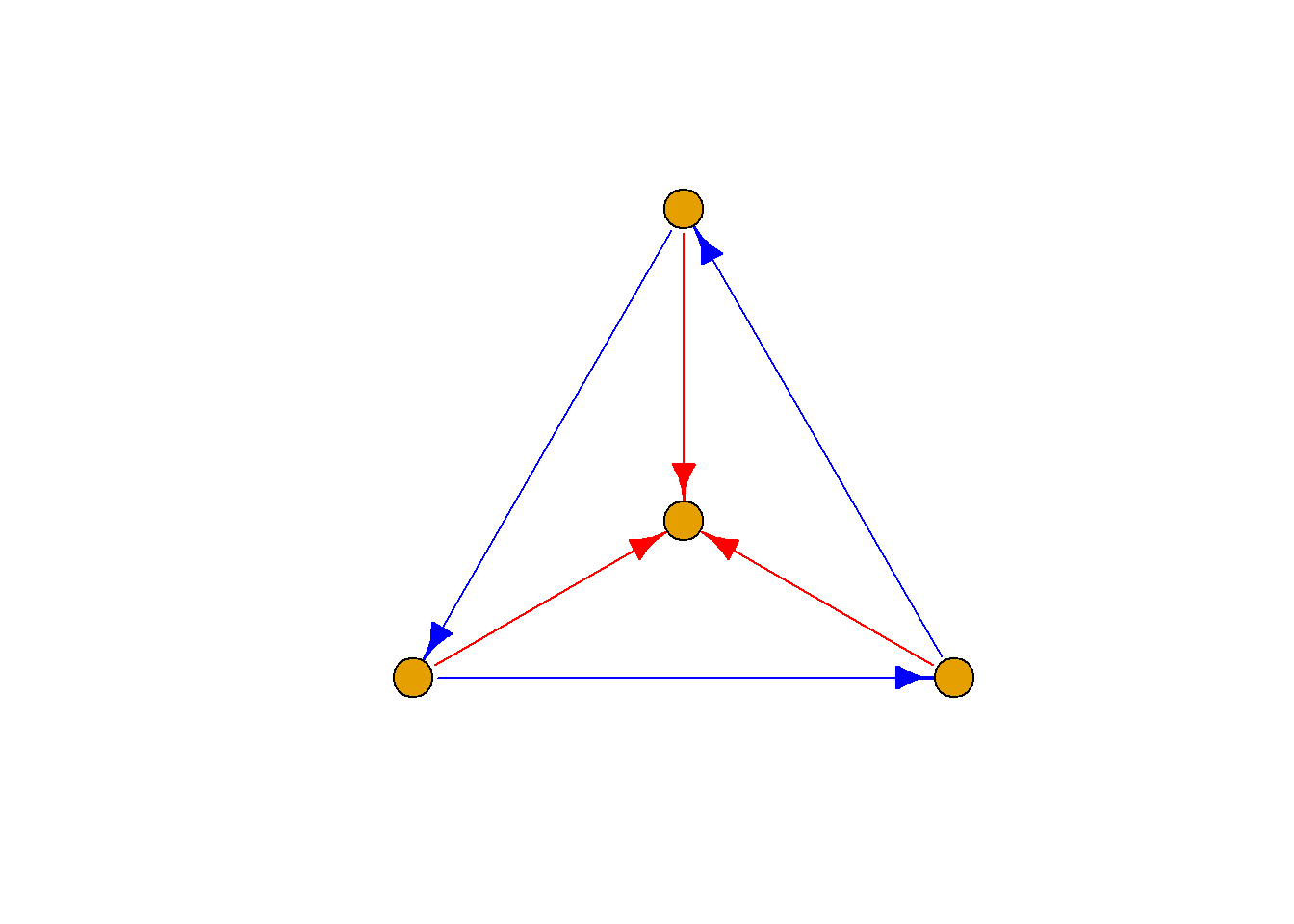
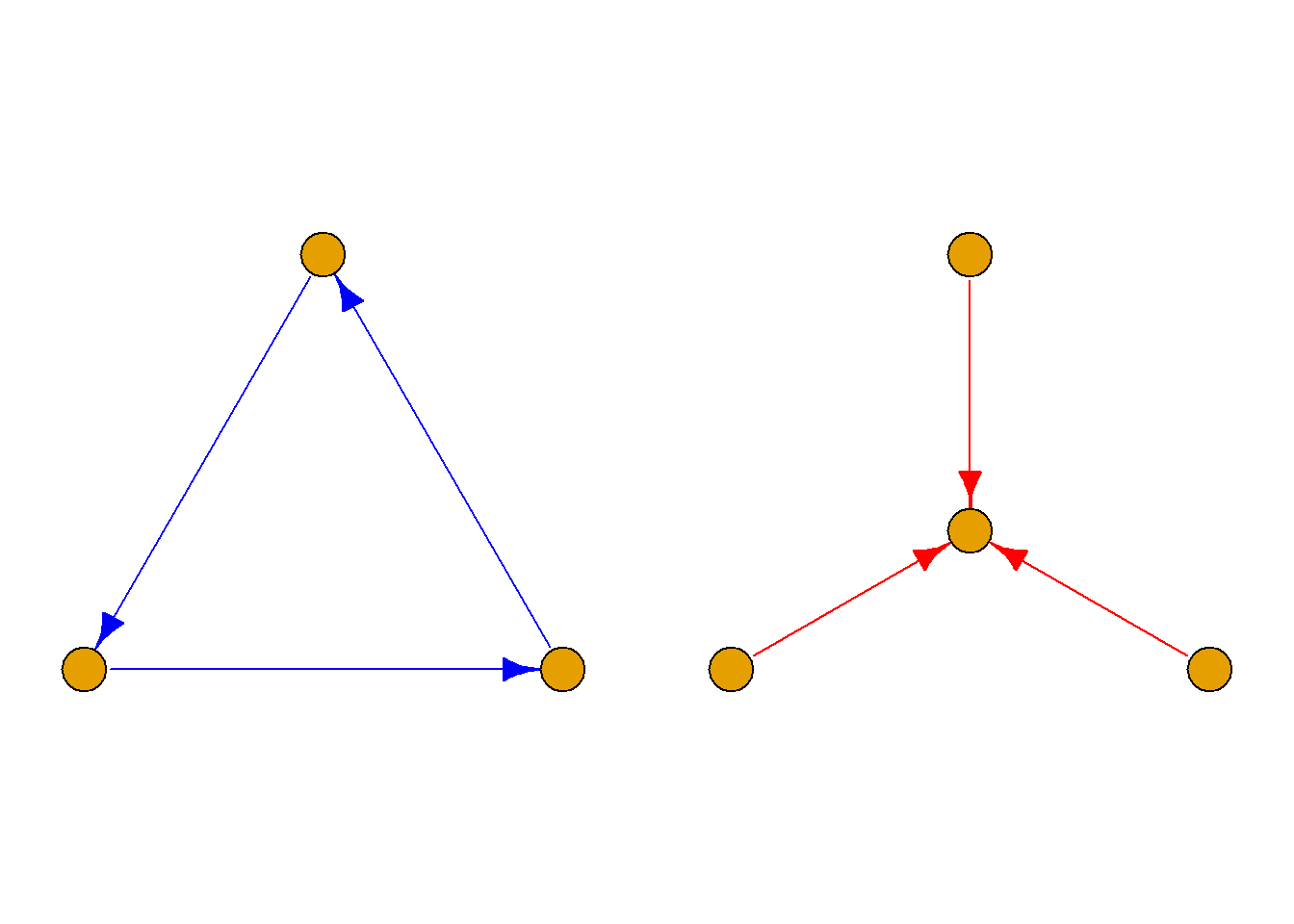
定义: 设图\(G={\langle}V, E{\rangle}\)是含有\(n\)个结点的简单图, 以\(V\)为结点集, 以所有能使\(G\)成为完全图\(K_n\)的添加边组成的图称为\(G\)的相对于完全图\(K_n\)的补图, 简称\(G\)的补图, 记为\(\bar{G}\).

显然, \(G\)和\(\bar{G}\)是互补的.

图的同构

定义: 给定无向图\(G={\langle}V, E{\rangle}\)和\(G^\prime={\langle}V^\prime, E^\prime{\rangle}\), 若存在双射函数\(f:V{\rightarrow}V^\prime\), 使得对于任意的\[e=(v_i, v_j){\in}E{\,\,\Leftrightarrow\,\, }e^\prime=(f(v_i), f(v_j)){\in}E^\prime, \]则称\(G\)和\(G^\prime\)同构, 记为\(G{\cong}G^\prime.\) 函数\(f\)称为是图\(G\)到图\(G^\prime\)的同构(映射).

定义: 给定有向图\(G={\langle}V, E{\rangle}和G^\prime={\langle}V^\prime, E^\prime{\rangle}\), 若存在双射函数\(f:V{\rightarrow}V^\prime\), 使得对于任意的\[e={\langle}v_i, v_j{\rangle}{\in}E\,\,{\Leftrightarrow}\,\,e^\prime={\langle}f(v_i), f(v_j){\rangle}{\in}E^\prime, \]则称\(G\)和\(G^\prime\)同构, 记为\(G{\cong}G^\prime\). 函数\(f\)称为是图\(G\)到图\(G^\prime\)的同构(映射).

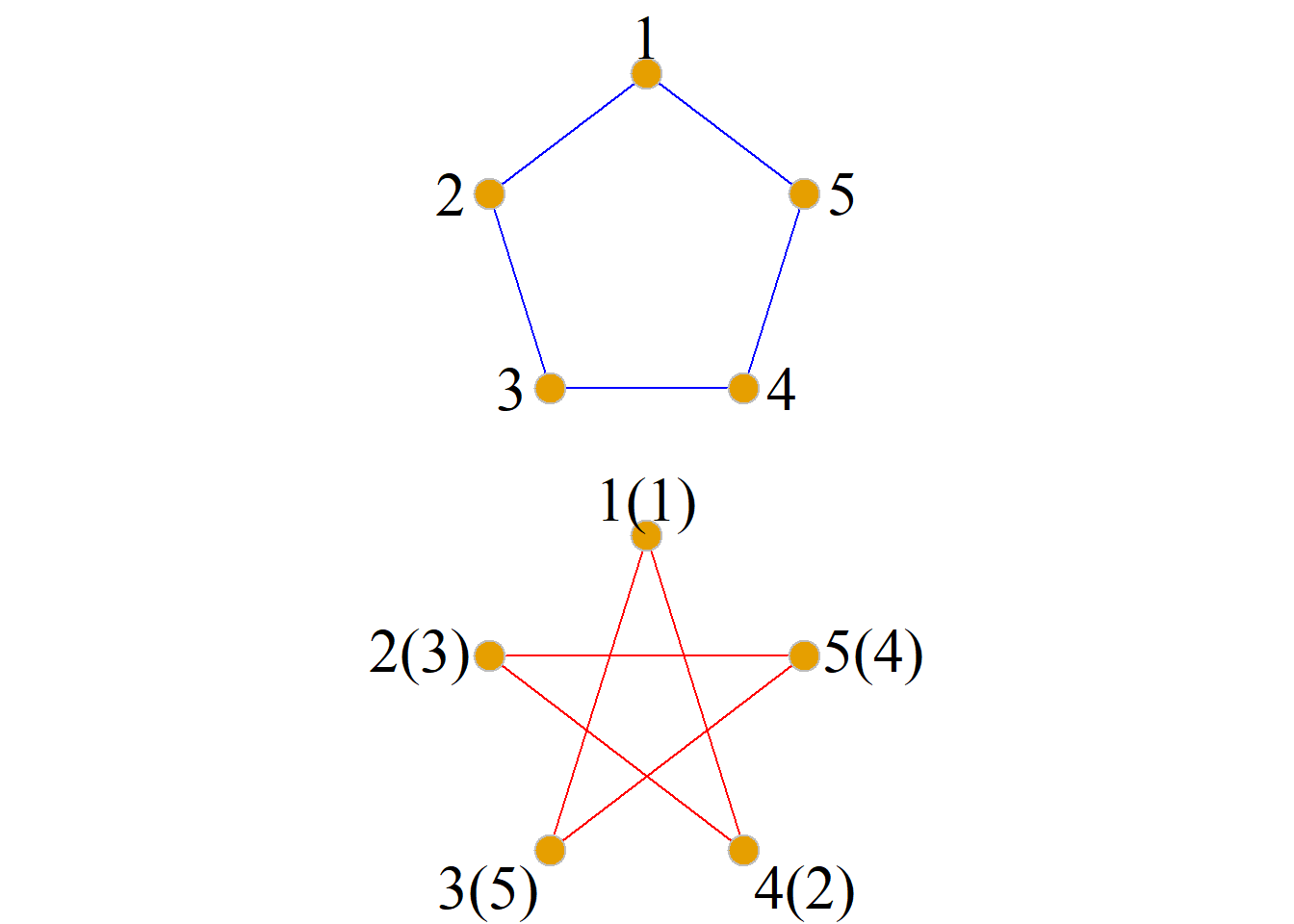
两图同构的充要条件是两图的结点和边分别存在着一一对应, 且保持相同的关联关系, 对于有向图这种对应还需保持边的方向.

其实, 图同构的直观意义是将其中一个图经过旋转、平移、拉伸等变形后可与另一图重合.

在图论中, 图同构是一个非常重要的问题.

图\(G_1\)和\(G_2\)是同构的. 因为可以建立以下对应关系, 即双射函数\(f\): \[\{a, b, c, d, e\}{\leftrightarrow}\{v_3, v_2, v_1, v_4, v_5\}\] \[(a, b){\leftrightarrow}(v_3, v_2)\] \[(a, c){\leftrightarrow}(v_1, v_3)\] \[(a, d){\leftrightarrow}(v_3, v_4)\] \[(b, c){\leftrightarrow}(v_2, v_1)\] \[(c, d){\leftrightarrow}(v_1, v_4)\] \[(d, e){\leftrightarrow}(v_4, v_5)\]

例: (a), (b)是同构的, 因为存在双射函数\(f\): \[\{a, b, c, d\}{\leftrightarrow}\{1, 2, 3, 4\}\] \[{\langle}a, b{\rangle}{\leftrightarrow}{\langle}1, 2{\rangle}\] \[{\langle}a, d{\rangle}{\leftrightarrow}{\langle}1, 4{\rangle}\] \[{\langle}b, c{\rangle}{\leftrightarrow}{\langle}2, 3{\rangle}\] \[{\langle}c, b{\rangle}{\leftrightarrow}{\langle}3, 2{\rangle}\] \[{\langle}d, c{\rangle}{\leftrightarrow}{\langle}4, 3{\rangle}\]

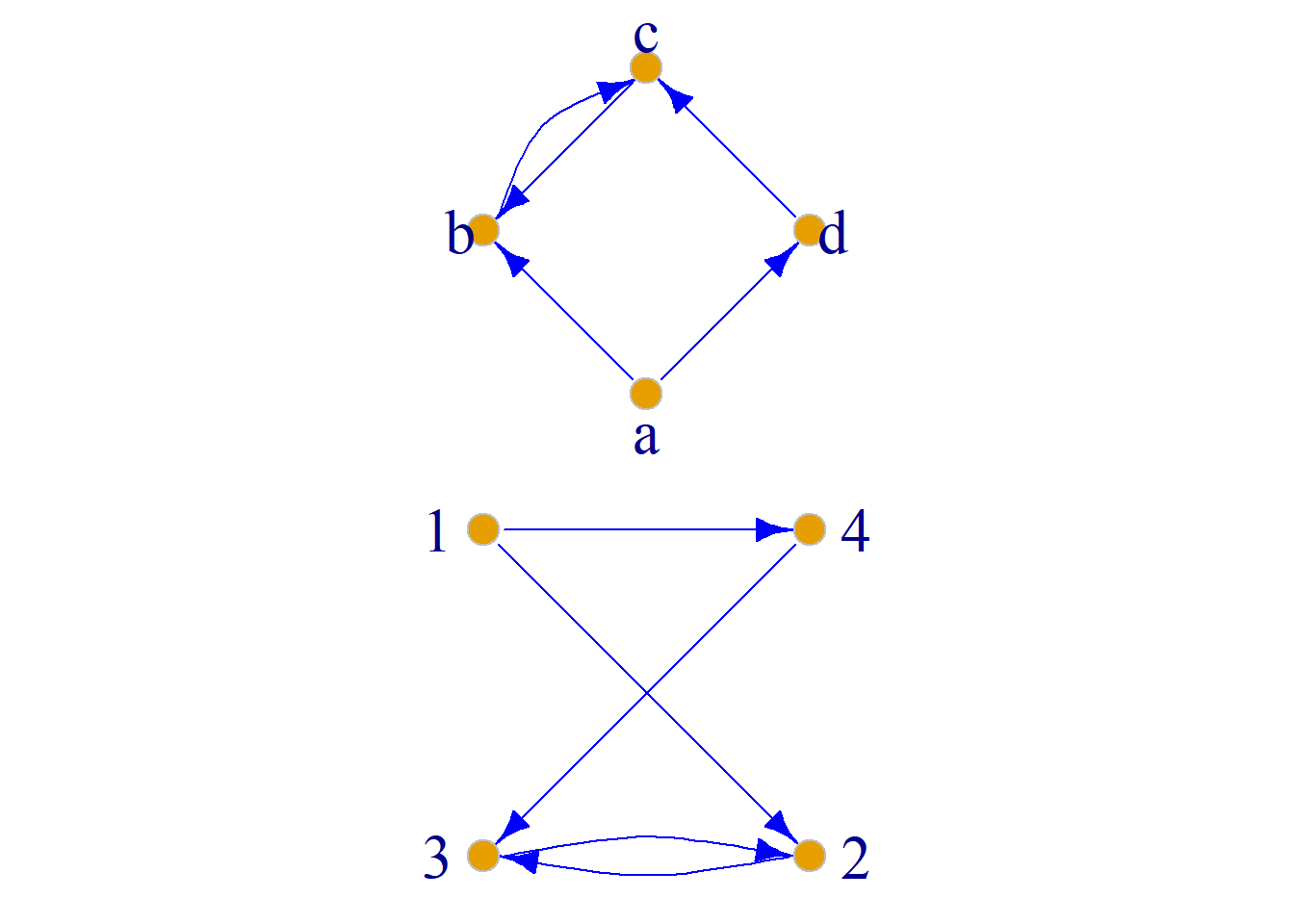
同构的两图具有如下的一些性质:

两图结点个数相同.
两图边数相等.
两图度数相同的结点个数相等.
设\(v{\in}V\), \(f(v)=u{\in}V^\prime\), 则\(d(v)=d(u)\)

这四个性质也是两图同构的必要条件, 但不是充分条件.也就是说两图同构必须满足这些性质, 当这些性质中的任一个没有被满足, 两图一定不同构.

两图都有5个结点和8条边, 但(a)有6度结点, 而(b)没有6度结点, 所以两图不同构.

这两个图都具有6个结点和9条边, 并且都具有2个2度结点、2个3度结点和2个4度结点, 然而两图却不同构.因为在(a)中2个3度结点是不邻接的, 但在(b)中2个3度结点是邻接的.

图的连通性

通路与回路

定义: 给定图\(G={\langle}V, E{\rangle}\), 设\(v_0, v_1, {\cdots}, v_k{\in}V, e_1, e_2, {\cdots}, e_k{\in}E\), 且\(e_i|(i=1, 2, {\cdots})\)以\(v_{i-1}\)和\({v_i}\)为端点(对有向图, \(v_{i-1}\)为\(e_i\)的始点, \(v_i\)为\(e_i\)的终点), 结点和边的交替序列\(v_0e_1v_1e_2{\cdots}e_kv_k\)称为结点\(v_0\)到结点\(v_k\)的通路或路径.

\(v_0\)和\(v_k\)分别称为通路的起点和终点, 边的数目\(k\)称为通路的长度.

当\(v_0=v_k\)时, 该通路称为回路或循环.

若通路中的所有边均不相同, 称此通路为简单通路或简单路径.若回路中的所有边均不相同, 称此回路为简单回路或简单循环.

若通路中的所有结点均不相同, 称此通路为基本通路或基本路径.

若回路中的所有结点均不相同(除起点和终点), 称此回路为基本回路或基本循环.

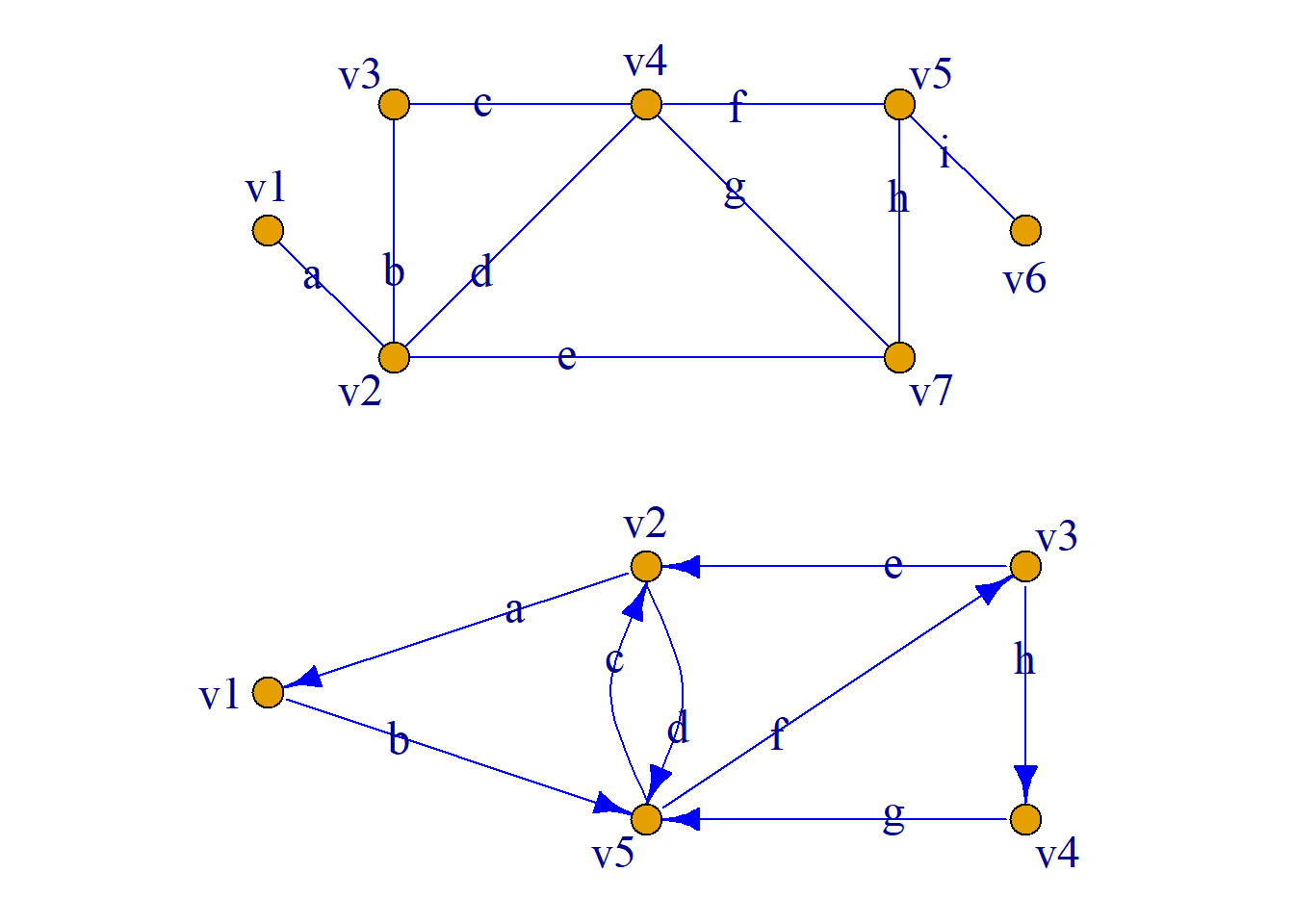
例: 如图所示.

在(a)中, \(v_1av_2bv_3cv_4dv_2ev_7\)是长度为5的简单通路,

\(v_1av_2ev_7hv_5iv_6\)是长度为4的基本通路.

在(b)中, \(v_1bv_5cv_2dv_5fv_3ev_2av_1\)是一条长度为6的简单回路,

\(v_5cv_2dv_5\)是一条长为2的基本回路.

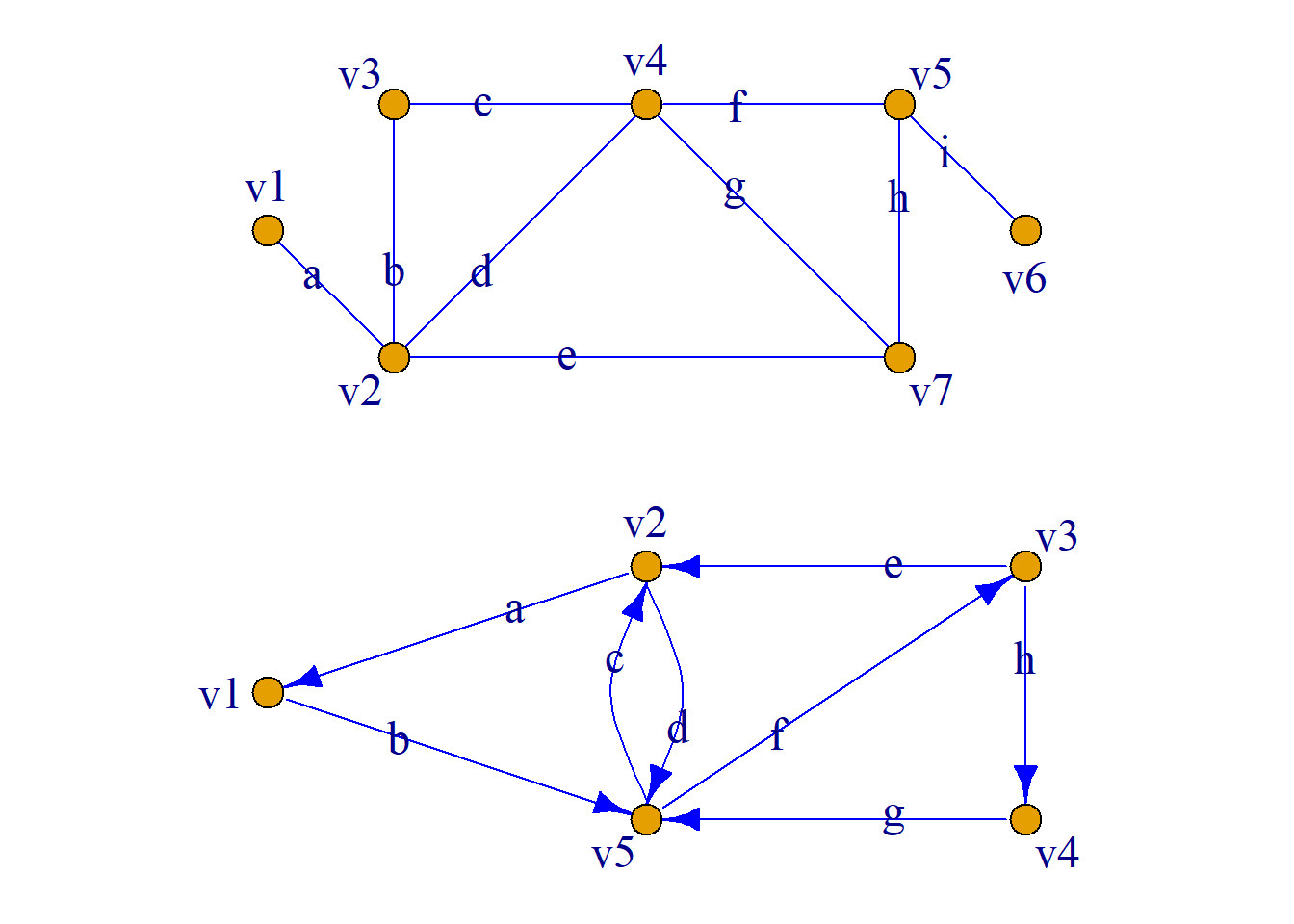
图(a)中, 简单通路\(v_1av_2bv_3cv_4dv_2ev_7\)可以用边的序列\(abcde\)表示, 或结点序列\(v_1v_2v_3v_4v_2v_7\)表示.

图(b)中, 简单回路\(v_1bv_5cv_2dv_5fv_3ev_2av_1\)可以用边的序列\(bcdfea\)来表示, 或结点序列\(v_1v_5v_2v_5v_3v_2v_1\)来表示.

定理: 在图\(G\)中, 若从结点\(v_i\)到结点\(v_j\)存在一条通路, 则必存在一条从结点\(v_i\)到结点\(v_j\)的基本通路.

定理: 在图\(G\)中, 若从结点\(v_i\)到结点\(v_i\)存在一条回路, 则必存在一条从结点\(v_i\)到结点\(v_i\)的基本回路.

定理: 在一个具有\(n\)个结点的图中, 有

任何基本通路的长度均不大于\(n-1\).
任何基本回路的长度均不大于\(n\).

图的连通性

定义: 给定图\(G={\langle}V, E{\rangle}\), \(v_i\)和\(v_j\)为\(G\)中的两结点, 若从\(v_i\)到\(v_j\)存在一条通路, 则称\(v_i\)到\(v_j\)是可达的.

规定\(G\)中任意结点到自身总是可达的.

对于无向图, 若从结点\(v_i\)到\(v_j\)是可达的, 则从结点\(v_j\)到\(v_i\)必然是可达的, 也就是两结点\(v_i\)和\(v_j\)互为可达.

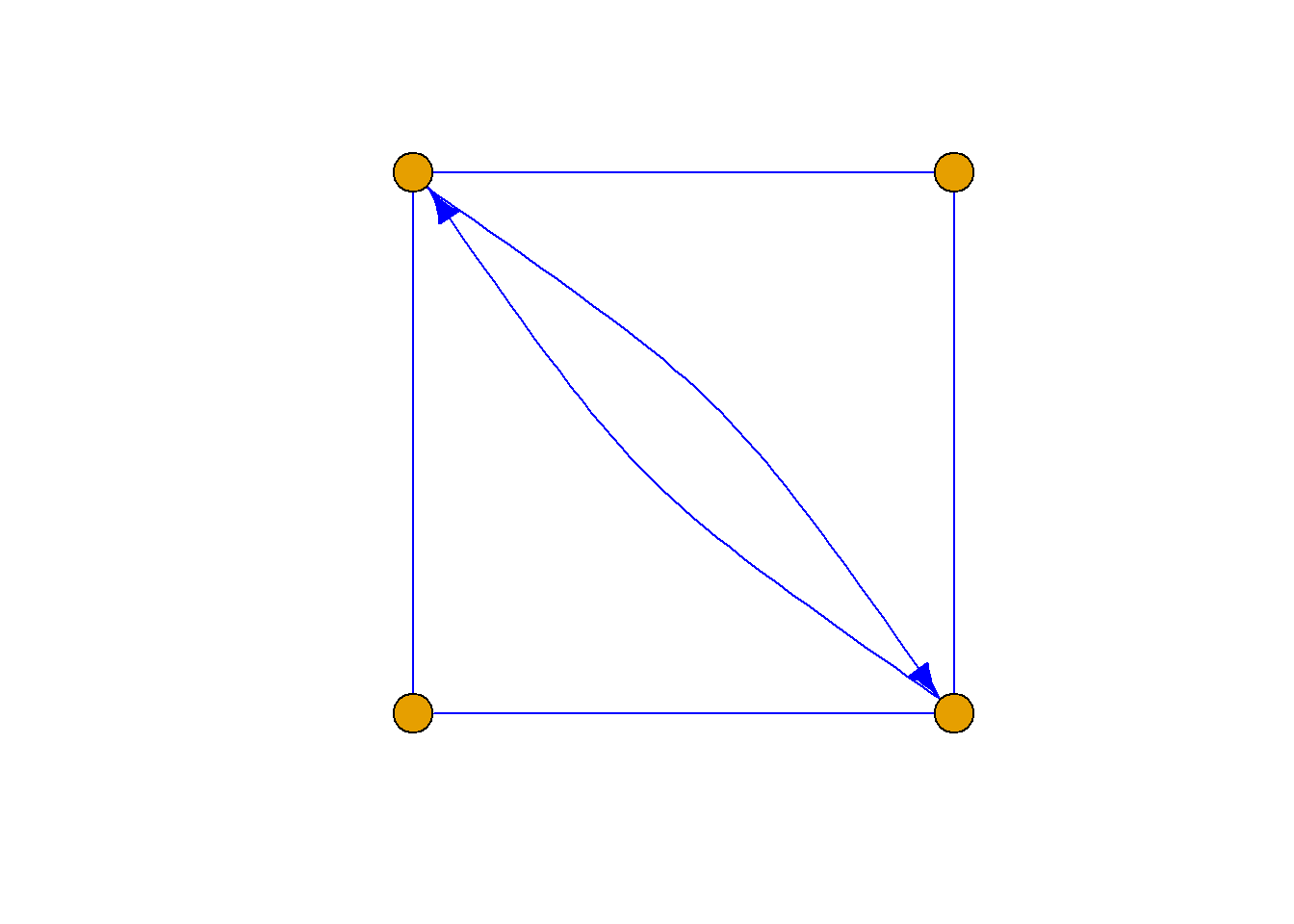
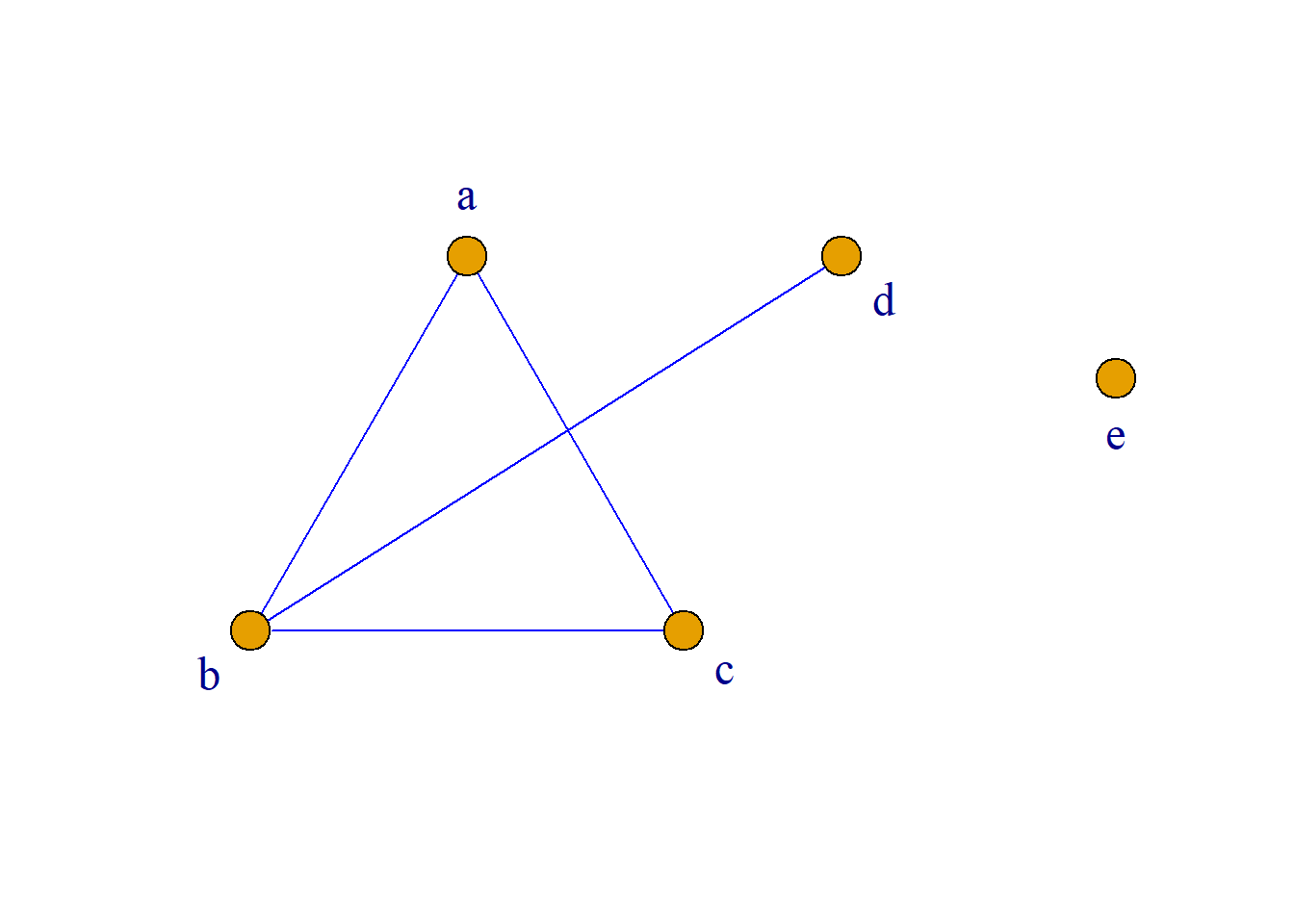
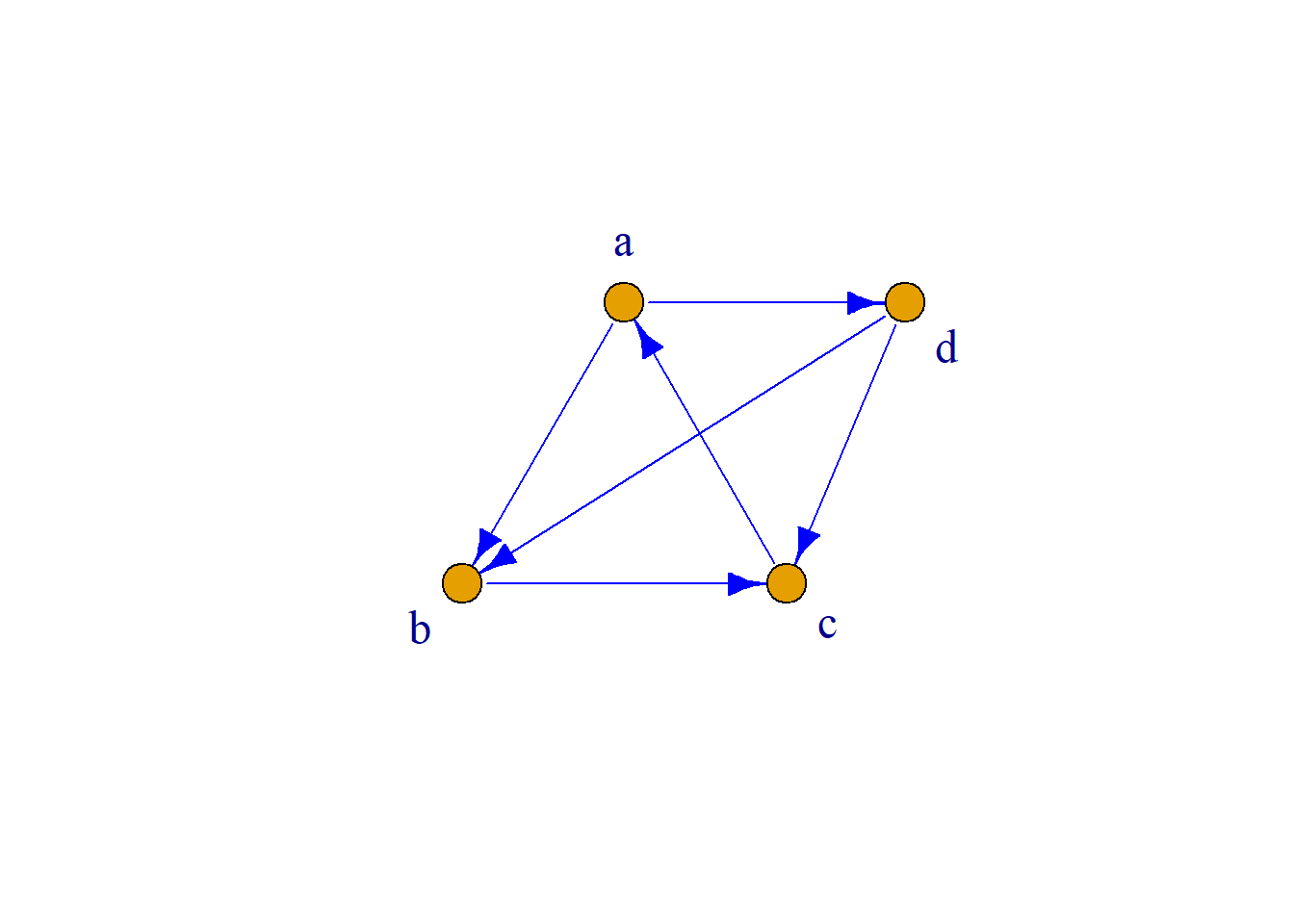
例: 如图\(G\)所示, \(a\)到\(d\)可达, \(d\)到\(a\)可达, \(a\)到\(d\)互为可达. \(b\)到\(e\)不可达.

对于有向图, 若从图中的结点\(v_i\)到\(v_j\)是可达的, 并不意味着从结点\(v_j\)到\(v_i\)也是可达的.

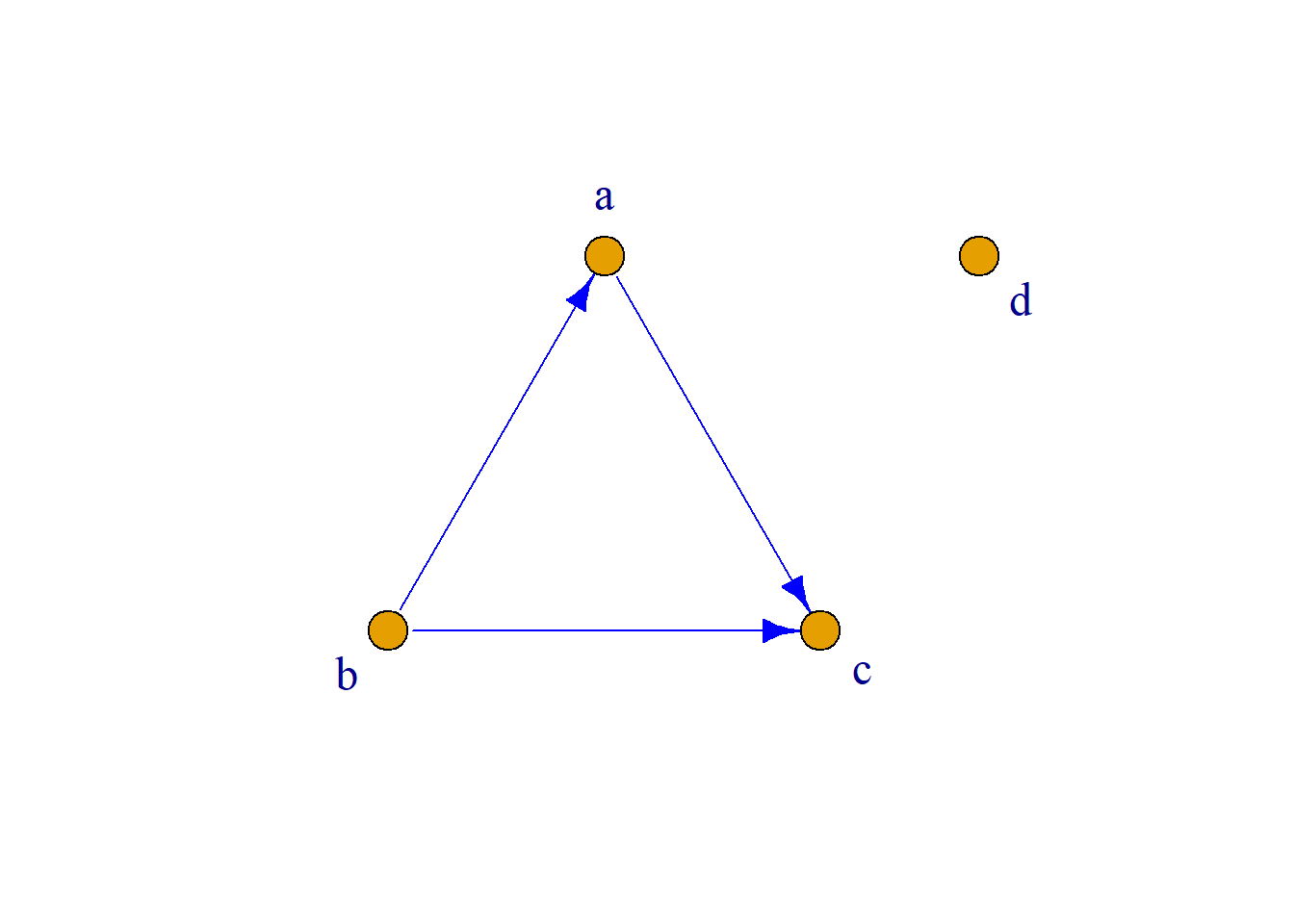
例: 如图\(G_1\)所示, \(a\)到\(c\)可达, \(c\)到\(a\)不可达.

定义: 对于图\(G={\langle}V, E{\rangle}\)中的任意两结点\(v_i\)和\(v_j\), 定义\(v_i\)到\(v_j\)的距离\(d[v_i, v_j]\)如下: \[ d[v_i, v_j]= \begin{cases} 0 & i=j \\ \infty & i{\neq}j, v_i到v_j不可达 \\ l & i{\neq}j, v_i到v_j可达 \\ \end{cases} \] 其中\(l\)是\(v_i\)到\(v_j\)的所有通路中长度最短的通路(称为短程线、测地线)的长度, 并称图\(G\)中任两点之间距离的最大值\[D=\max_{v_i, v_j{\in}V}d[v_i, v_j]\]为图的直径.

距离\(d[v_i, v_j]\)满足下列性质:

(1)\(d[v_i, v_j]{\geq}0\), 对于图中的任意两点\(v_i\)和\(v_j\).

(2)\(d[v_i, v_k]+d[v_k, v_j]{\geq}d[v_i, v_j]\), 对于图中的任意三点\(v_i\), \(v_k\)和\(v_j\).

(3)\(d[v_i, v_j]=d[v_j, v_i]\), 对于无向图中的任意两点\(v_i\)和\(v_j\).

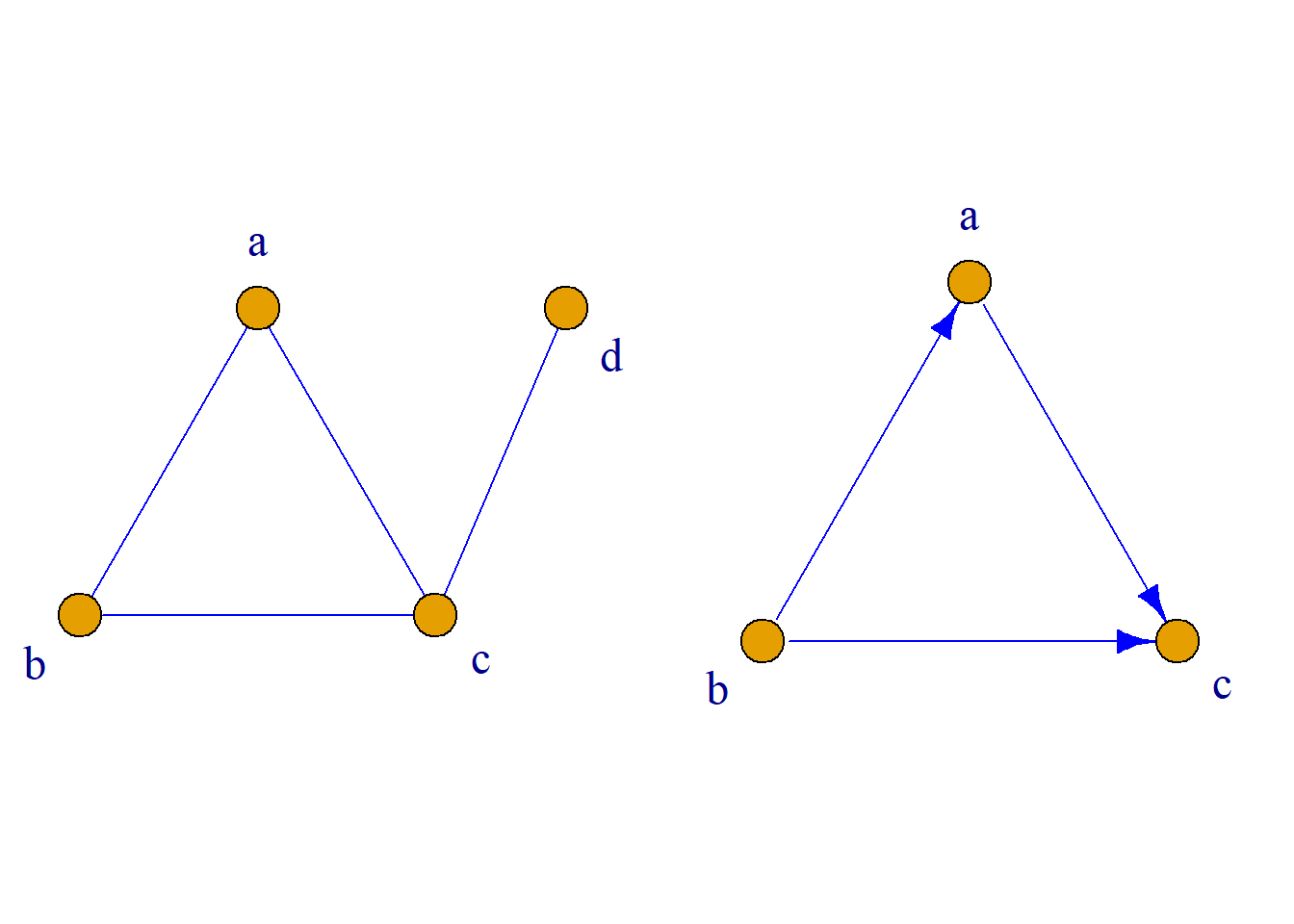
例: 如图\(G_1\)所示,

\(d[a, d]=2\), \(d[d, a]=2\),

\(a\)和\(d\)互为可达.

如图\(G_2\)所示,

\(d[a, c]=1\), \(d[c, a]={\infty}\),

\(a\)到\(c\)可达, \(c\)到\(a\)不可达.

例: 如图\(G\)所示, \(a\)和\(d\)互为可达, 但

\(d[a, d]=2\), \(d[d, a]=3\).

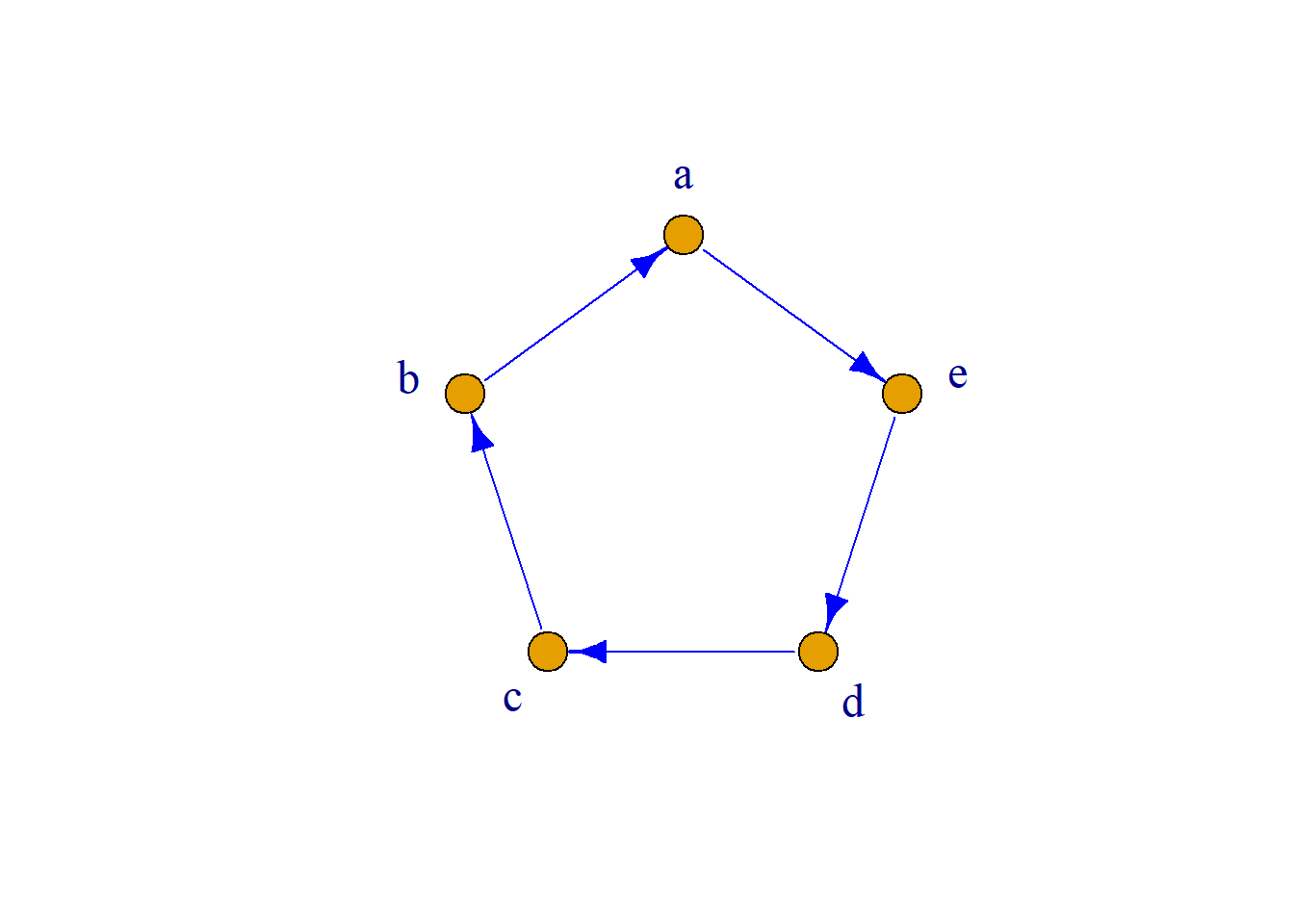
定义: 设\(G={\langle}V, E{\rangle}\)是无向图, 若\(G\)中任意两个结点都是相互可达的, 则称无向图\(G\)是连通的, 否则称是非连通的.

无向图被划分为两类: 连通图和非连通图.

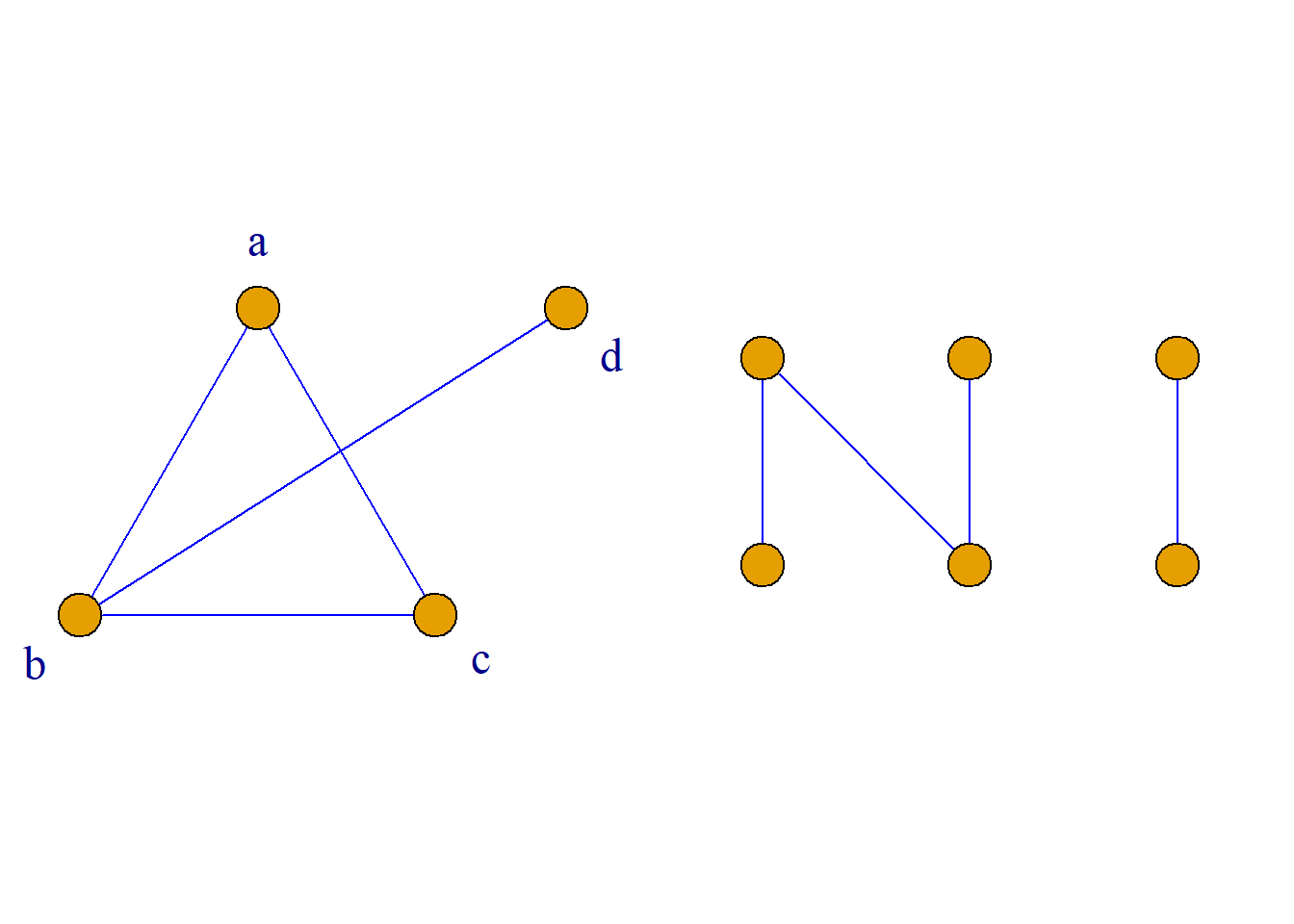
定义: 设\(G^\prime\)是无向图\(G\)的子图, 若\(G^\prime\)是连通的, 则称\(G^\prime\)是无向图\(G\)的连通子图.

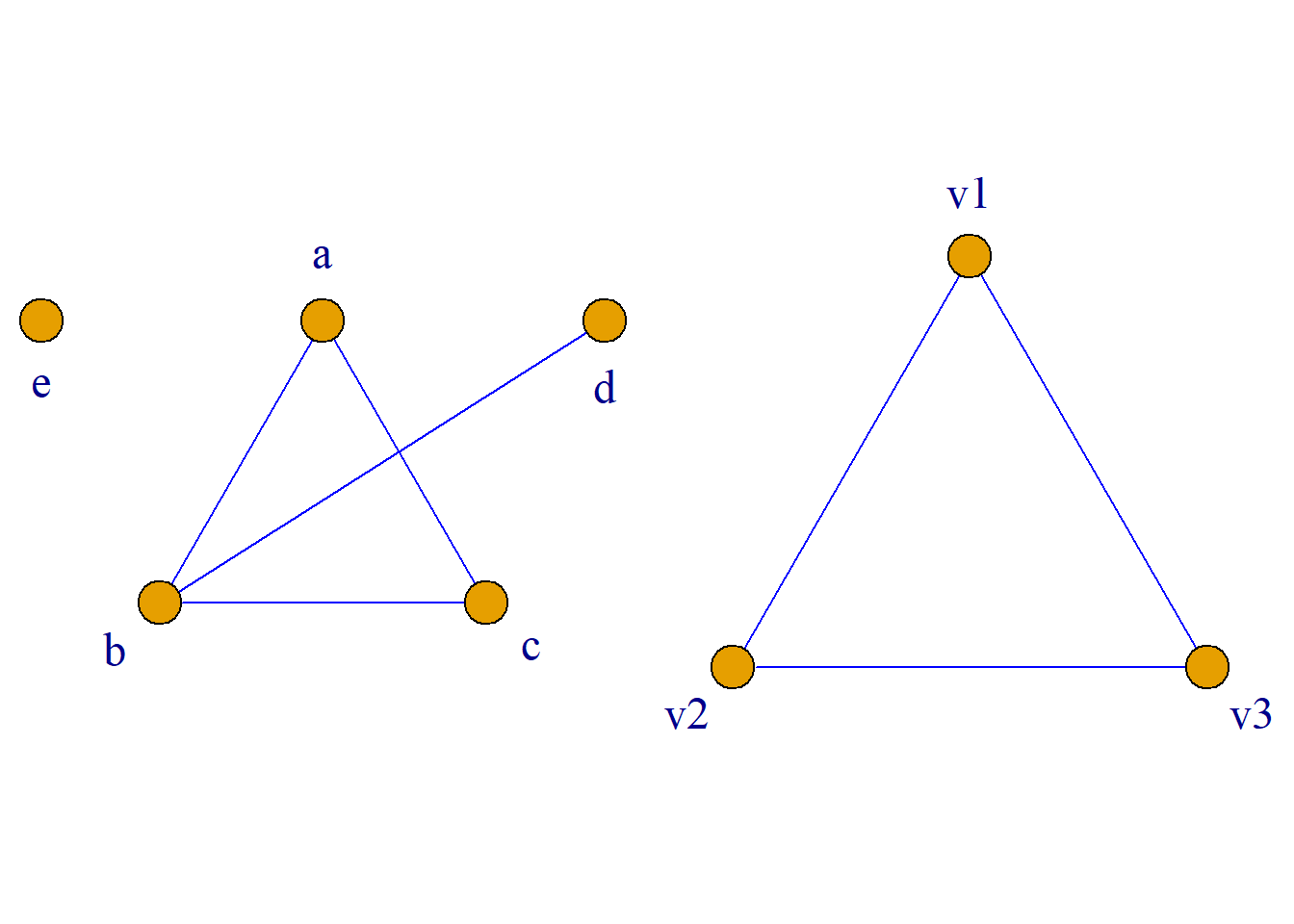
定义: 设\(G^\prime\)是无向图\(G\)的连通子图, 若\(G^\prime\)不包含在\(G\)的任何更大的连通子图中, 则称\(G^\prime\)是无向图\(G\)的连通分支(极大连通子图).

若一个无向图\(G\)是连通的, 则它只有一个连通分支就是\(G\)本身;若一个无向图\(G\)是非连通的, 则它至少有两个连通分支. 一个无向图的连通分支数常记为\(p(G)\)(或\(w(G)\)).

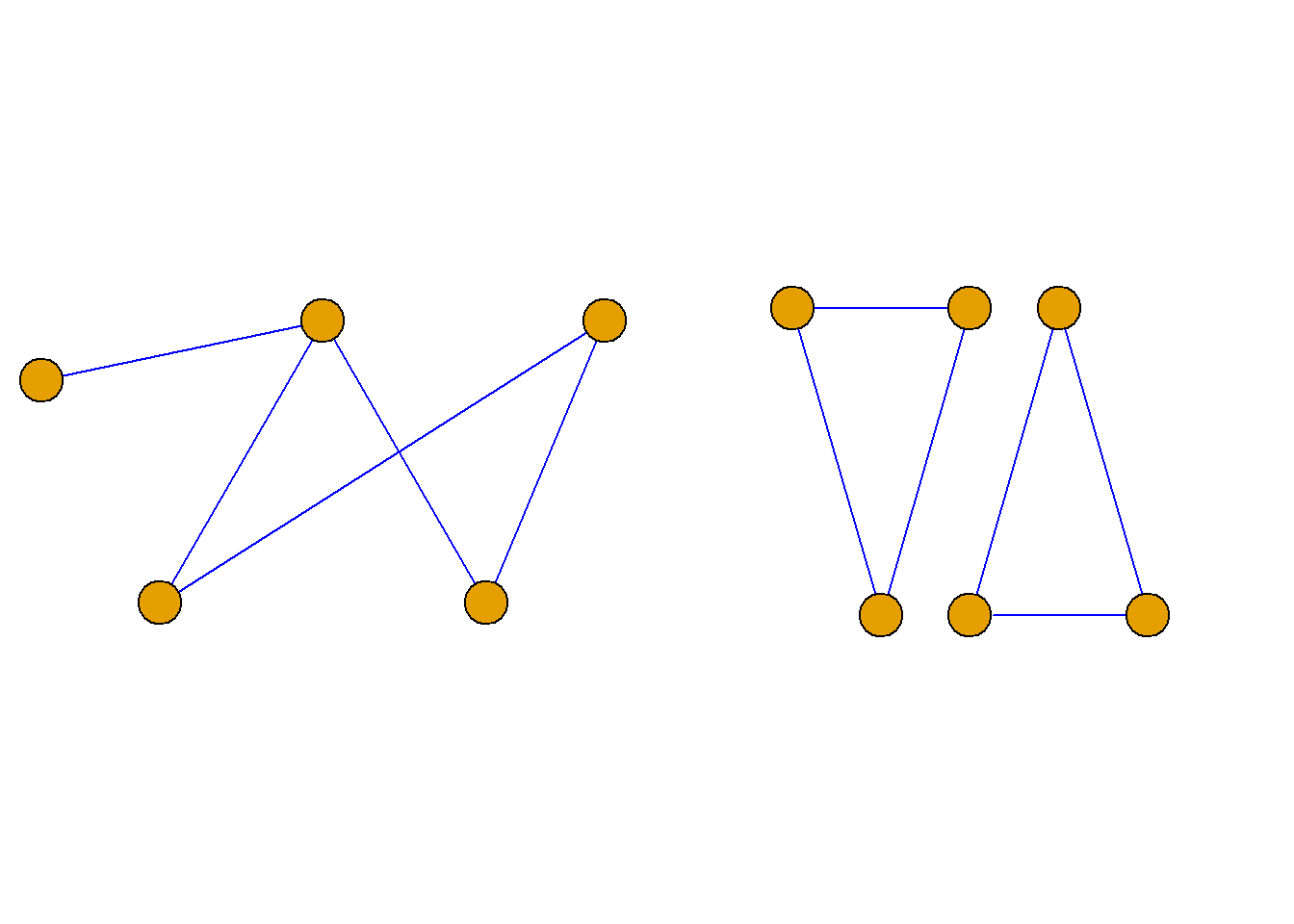
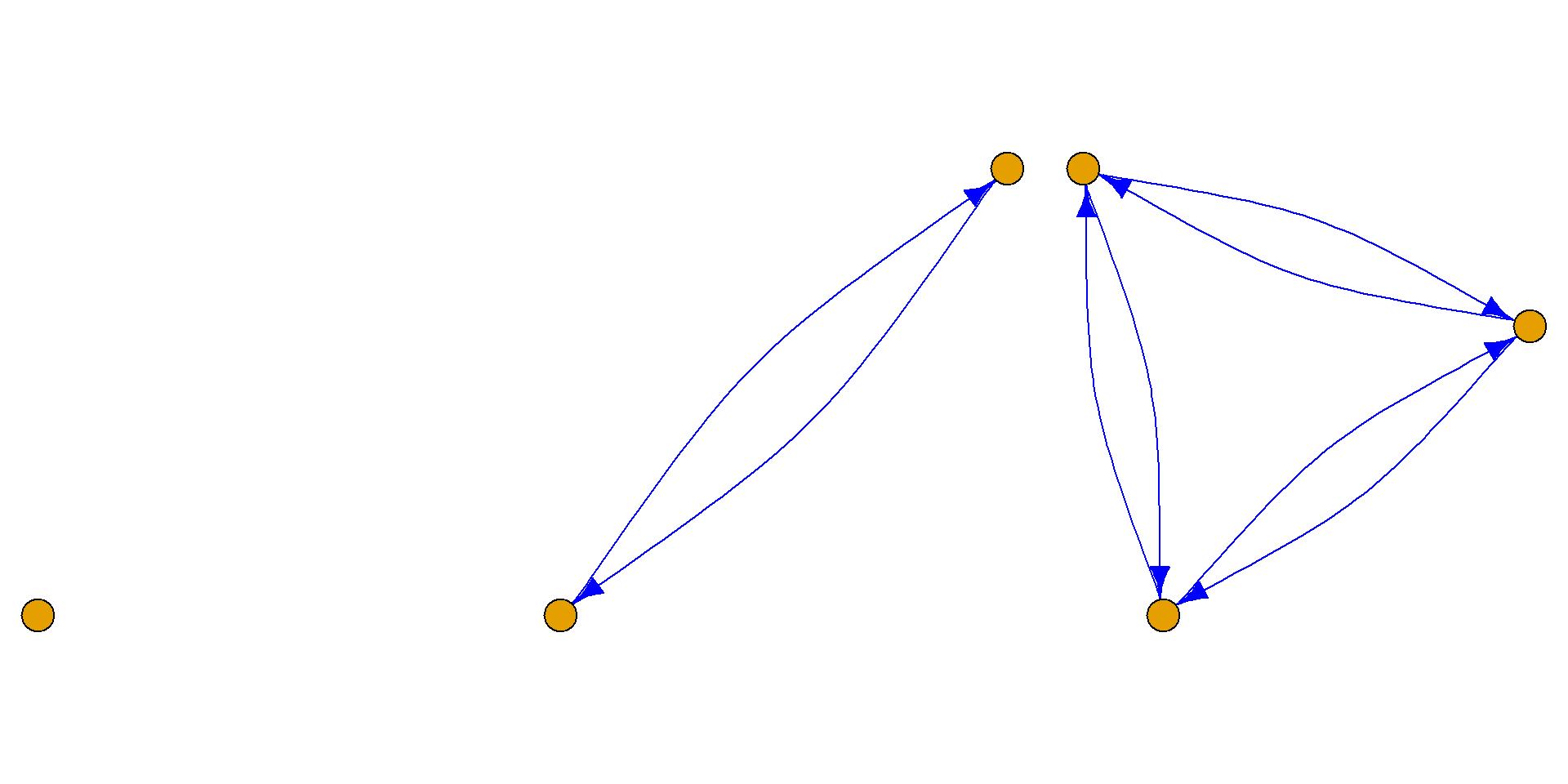
G₁是连通的, 仅有一个连通分支, 即它自身;G₂是非连通的, G₂含有两个连通分支(a)和(b)

定义: 设\(G={\langle}V, E{\rangle}\)是有向图, 那么:

若略去\(G\)中所有边的方向, 所得的无向图是连通的, 则称有向图\(G\)是弱连通的.
若\(G\)中任何两个结点之间, 至少有一个结点到另一个结点是可达的, 则称有向图\(G\)是单向连通的.
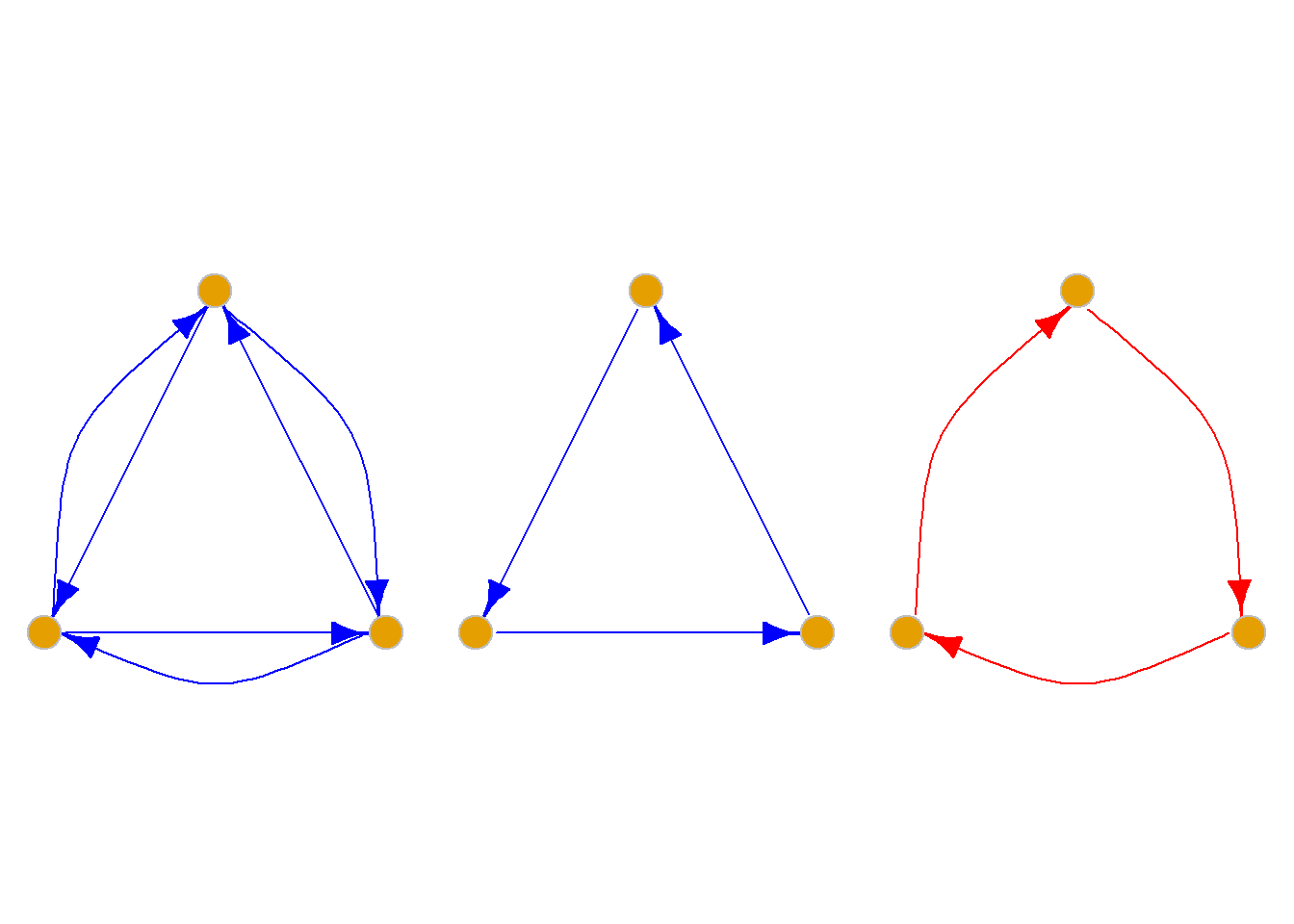
若\(G\)中任何两个结点之间都是相互可达的, 则称有向图\(G\)是强连通的.

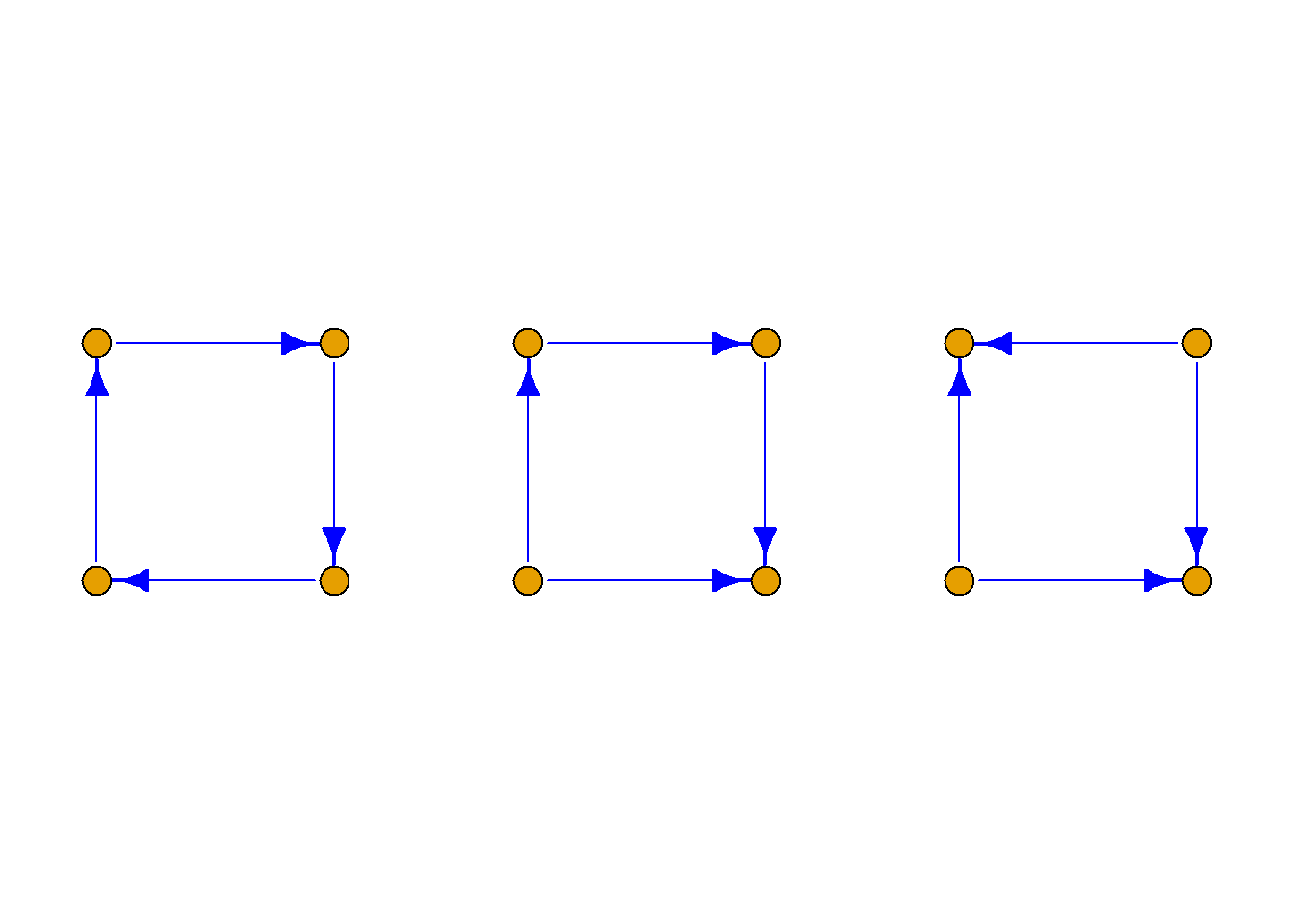
G₁是弱连通的, 但不是单向连通的(c和d互为不可达)和强连通(c到d不可达); G₂是非连通的.

从左到右分别是强连通、单向连通和弱连通. 对于有向图: 若有向图是强连通的, 则必是单向连通的; 若有向图是单向连通的, 则必是弱连通的. 但这两个结论的逆不真.

定理: 有向图\(G\)是强连通的, 当且仅当\(G\)中存在一回路, 它经过图中每个结点至少一次.

右图是强连通图. 经过每个结点的回路: bcadb.

定义: 设\(G^\prime\)是有向图\(G\)的具有某种性质的子图, 若\(G\)没有其它的子图具有这种性质且以\(G^\prime\)为其真子图, 则称\(G^\prime\)是\(G\)的具有该性质的极大子图.

左上：原图；

右上：具有强连通性质极大子图；

左下：具有单向连通性质极大子图；

右下：具有单向连通性质极大子图.

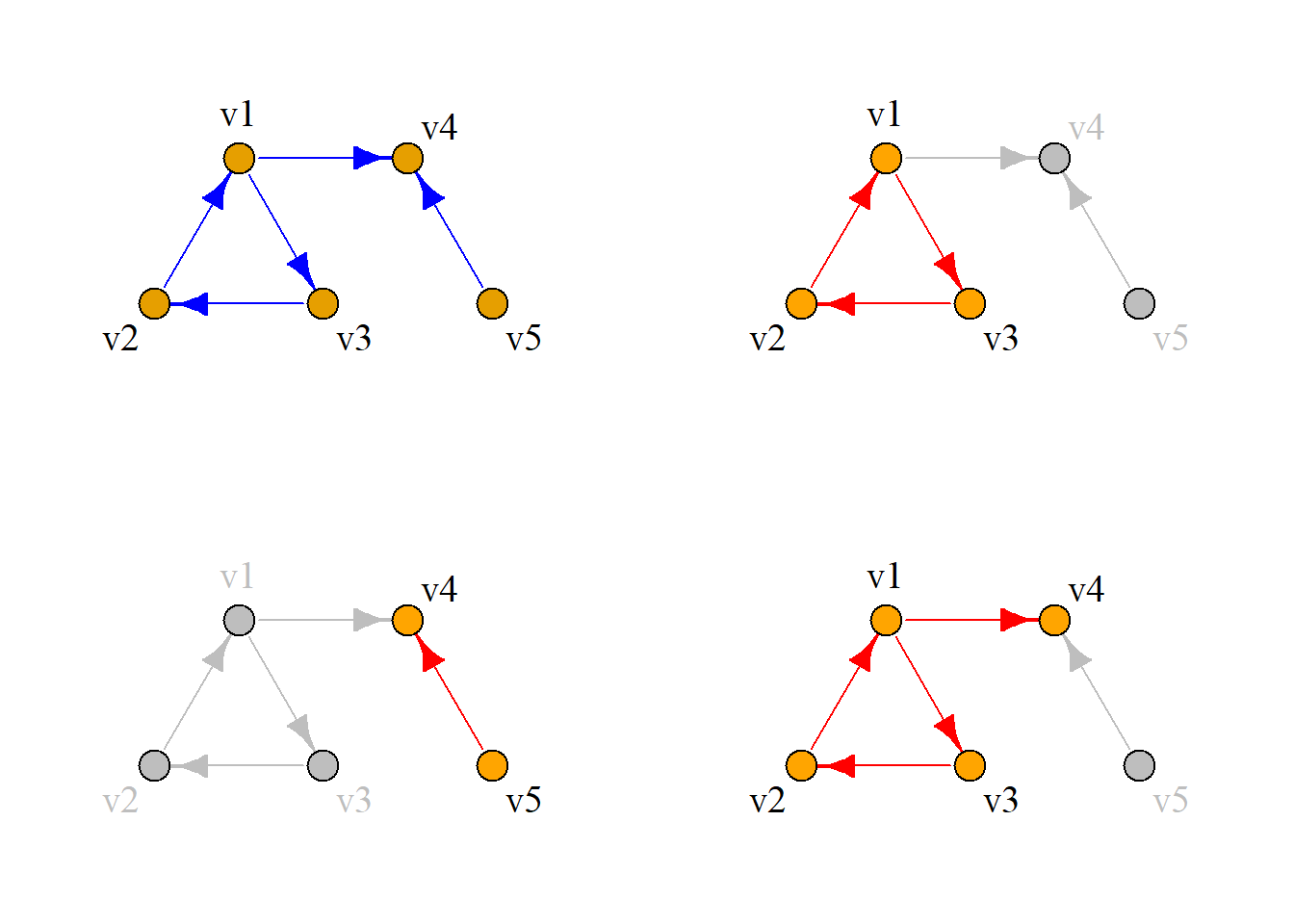
定义: 在有向图\(G\)中, 具有强连通性质的极大子图称为强分图(强连通分支);具有单向连通性质的极大子图称为单向分图(单向连通分支);具有弱连通性质的极大子图称为弱分图(弱连通分支).

\(G[\{v_1, v_2, v_3\}]\), \(G[\{v_4\}]\), \(G[\{v_5\}]\), \(G[\{v_6\}]\)是强分图;

\(G[\{v_1, v_2, v_3, v_4, v_5\}]\), \(G[\{v_5, v_6\}]\)是单向分图;

\(G[\{v_1, v_2, v_3, v_4, v_5, v_6\}]\)是弱分图.

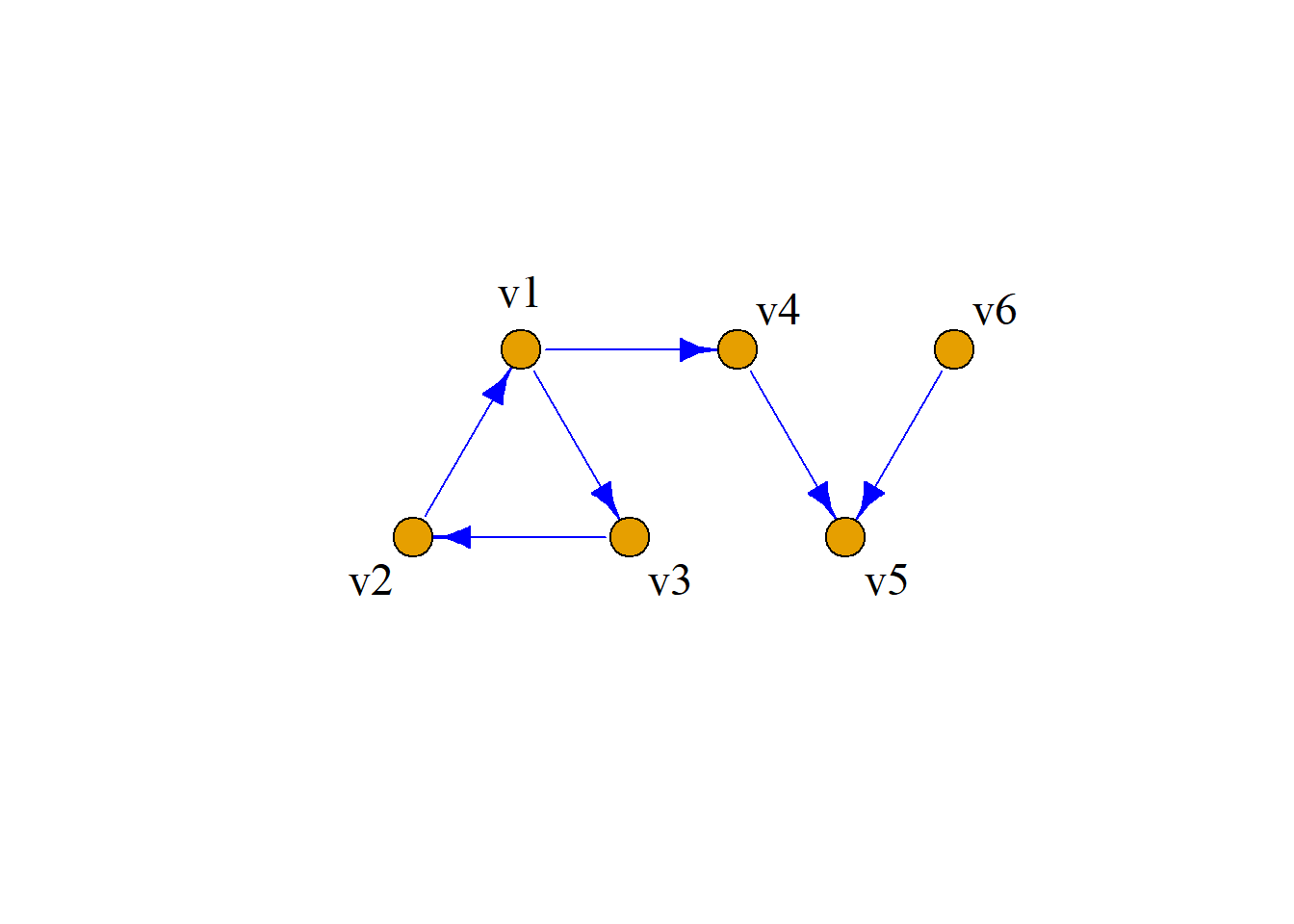
\(G[\{v_1\}]\), \(G[\{v_2\}]\), \(G[\{v_3\}]\), \(G[\{v_4\}]\), \(G[\{v_5, v_6, v_7\}]\)是强分图;

\(G[\{v_1, v_2, v_3\}]\), \(G[\{v_1, v_3, v_4\}]\), \(G[\{v_5, v_6, v_7\}]\)是单向分图;

\(G[\{v_1, v_2, v_3, v_4\}]\), \(G[\{v_5, v_6, v_7\}]\)是弱分图.

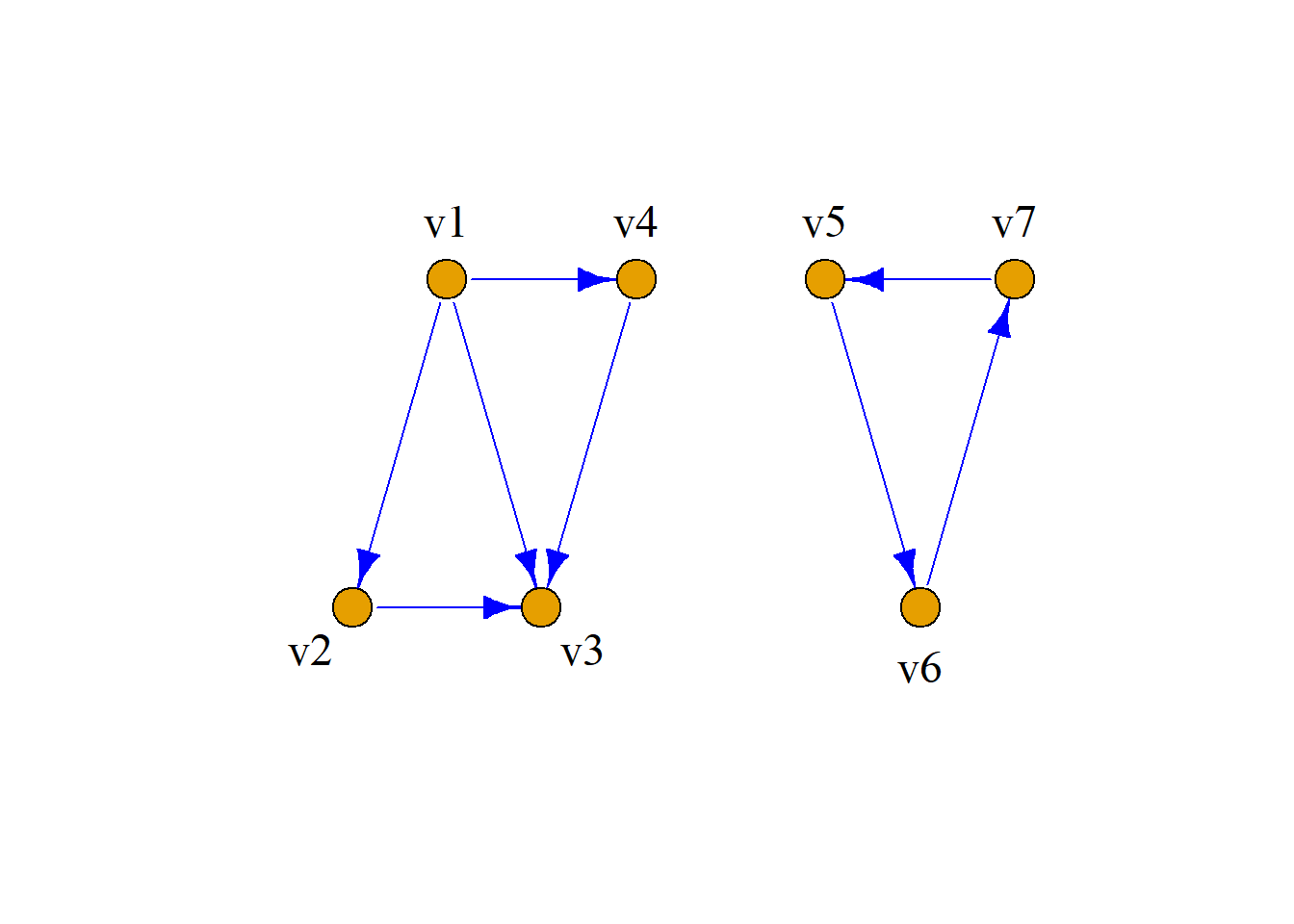
定理: 在简单有向图\(G={\langle}V, E{\rangle}\)中, 任一结点都处于且只处于一个强分图中;每个结点和每条边都仅处于一个弱分图中;每个结点和每条边都至少处于一个单向分图中.

连通度

连通是图的一个比较常见的问题, 主要用于判断任意两个结点的连接状态, 特别是用于检测网络连接与电路连接的问题中, 运用比较广.

定义: 设无向图\(G={\langle}V, E{\rangle}\)是连通的, 如果有结点子集\(V^\prime{\subset}V\), 使得在图\(G\)中删除了\(V^\prime\)后, 所得到的子图\(G-V^\prime\)是非连通的, 而在图\(G\)中删除\(V^\prime\)的任何真子集所得到的子图仍是连通的, 那么称\(V^\prime\)为\(G\)的一个点割集.

若图\(G\)的某一点割集仅有一个结点\(v\), 则称该结点\(v\)为割点.

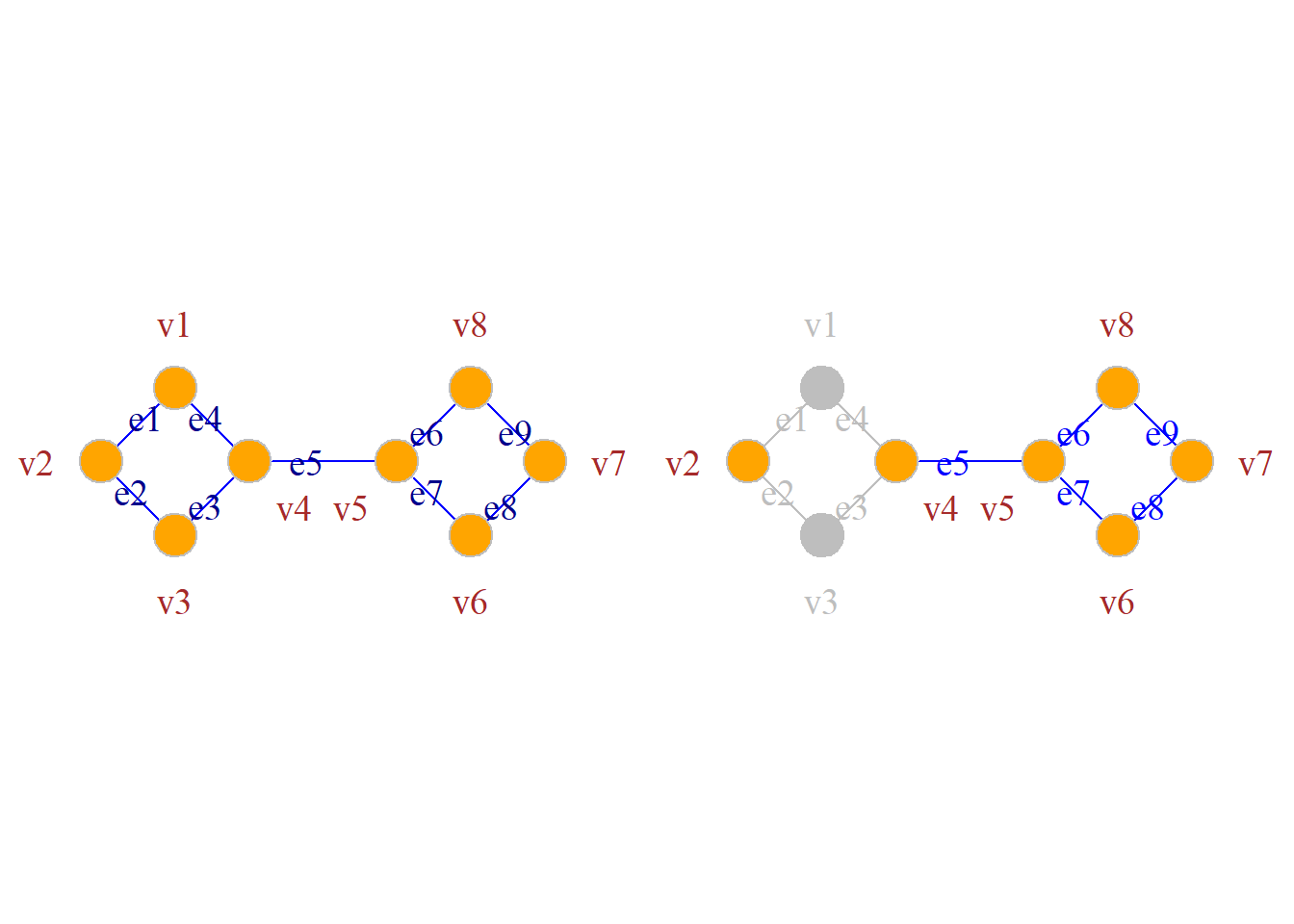
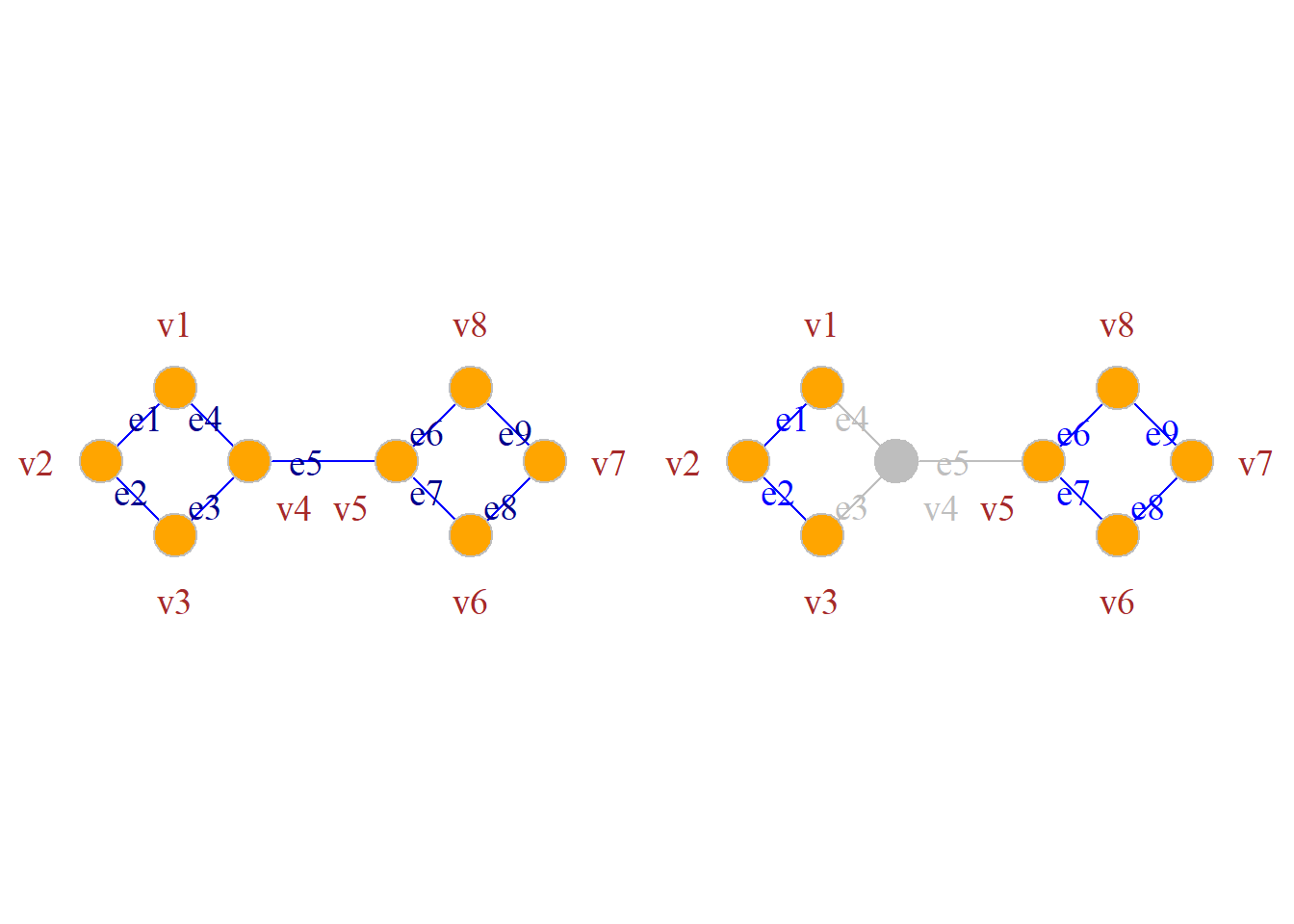
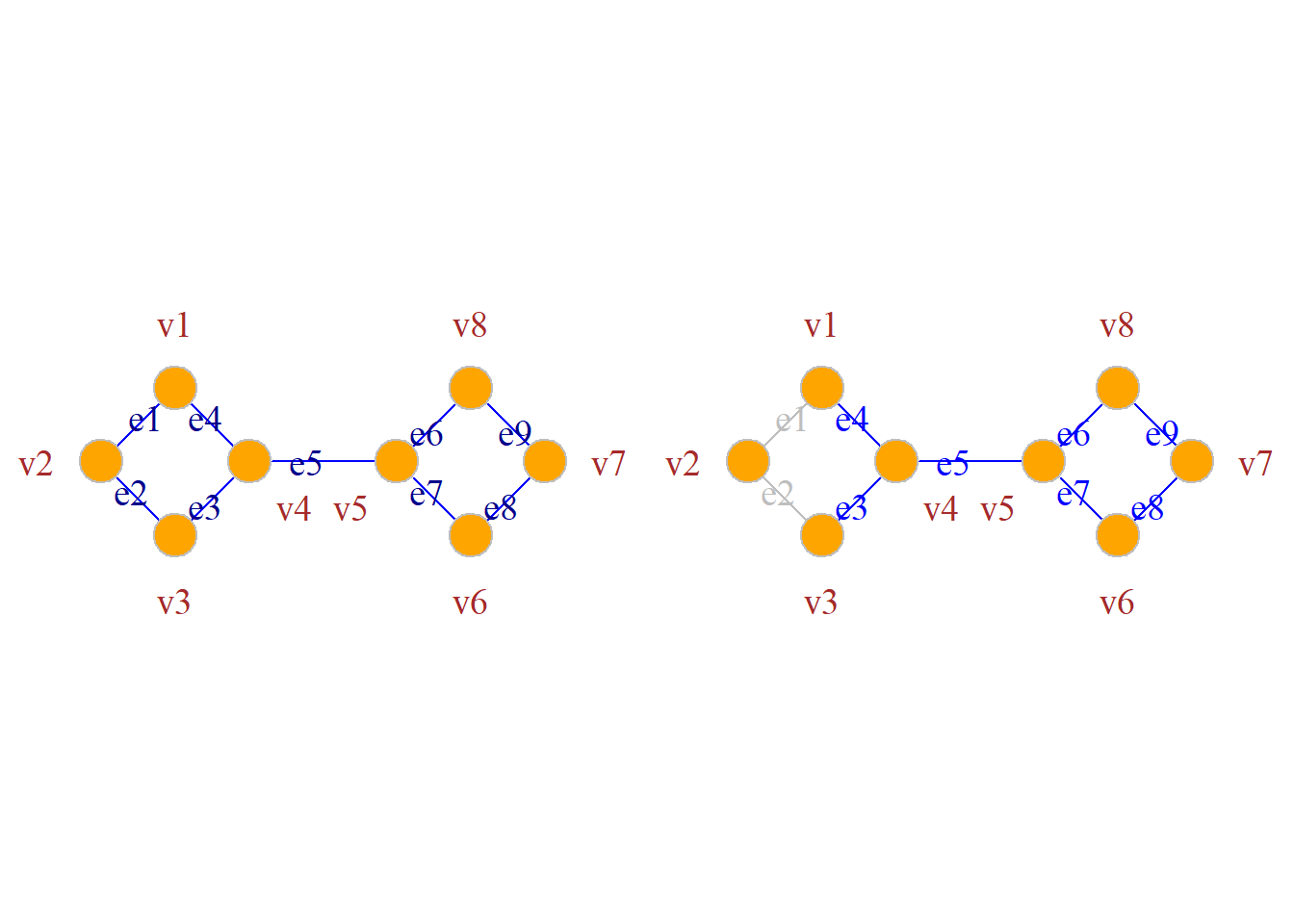
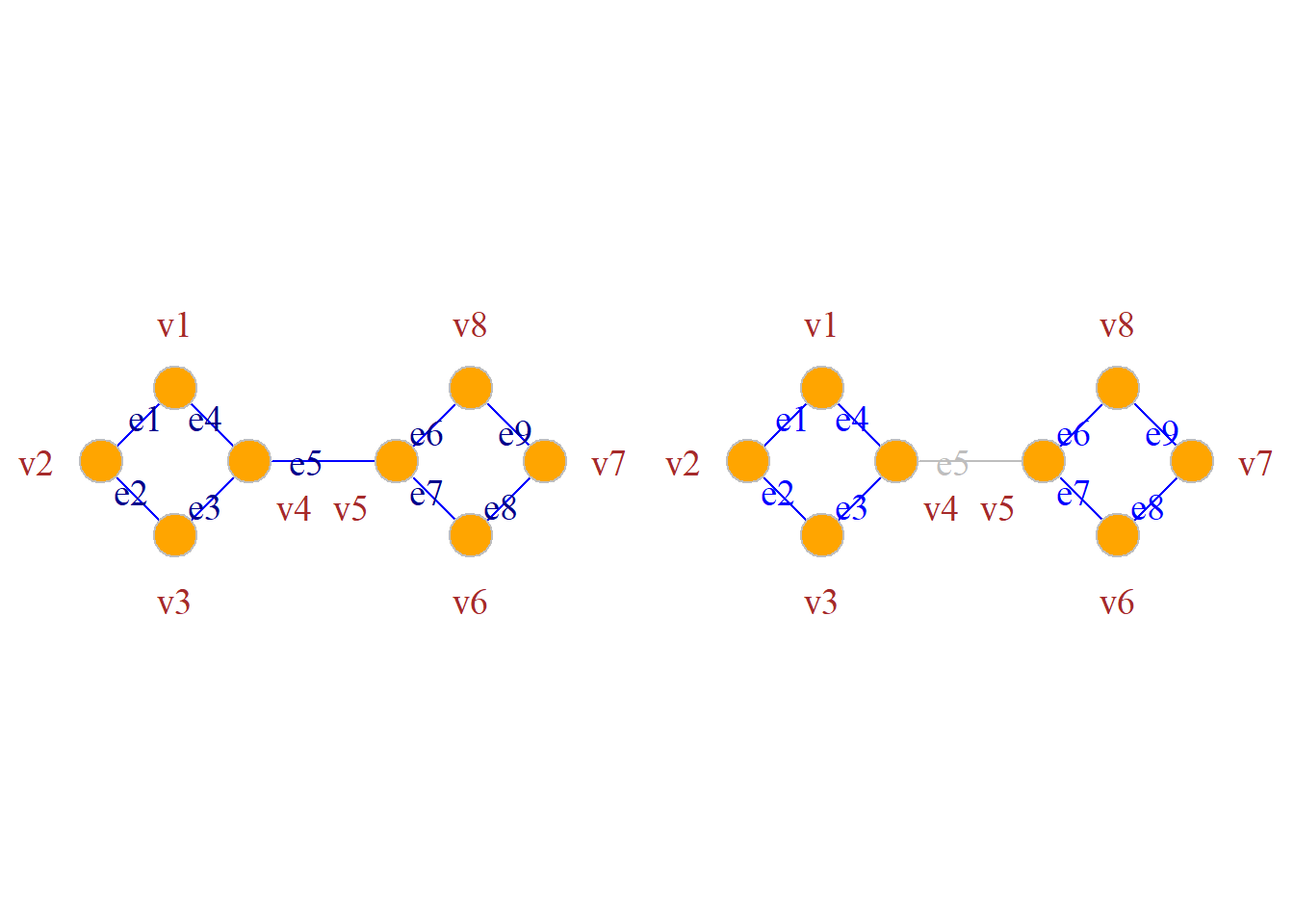
定义: 设无向图\(G={\langle}V, E{\rangle}\)是连通的, 若有边子集\(E^\prime{\subset}E\), 使得在图\(G\)中删除了\(E^\prime\)后, 所得到的子图\(G-E^\prime\)是非连通的, 而在图\(G\)中删除\(E^\prime\)的任何真子集所得到的子图仍是连通图, 则称\(E^\prime\)为\(G\)的一个边割集.

若图\(G\)的某一边割集仅有一条边\(e\), 则称该边\(e\)为割边或桥.

定义: 设无向图\(G={\langle}V, E{\rangle}\)是连通的, 定义\(G\)的点连通度\({\chi}(G)\)如下:

\({\chi}(G)=\min\{|V^\prime|\, \, |V^\prime\)为\(G\)的点割集或者\(V^\prime\)使\(G-V^\prime\)成为平凡图}

点连通度\({\chi}(G)\)是由连通图\(G\)产生非连通图需要删除的点的最少数目.

若\(G\)是非连通的, 则因为不用删除任何结点\(G\)就是非连通的, 因而, 规定其点连通度 \[{\chi}(G)=0.\]

定义: 设无向图\(G={\langle}V, E{\rangle}\)是连通的, 定义\(G\)的边连通度\({\lambda}(G)\)如下:

\[ \lambda(G)= \begin{cases} 0 & G是非连通图\\ \min\{|E^\prime|\, \, |E^{\prime}为边割集\} & 否则 \end{cases} \]

边连通度\({\lambda}(G)\)是由连通图\(G\)产生非连通图需要删除边的最少数目.

若\(G\)是非连通的, 则因为不用删除任何边\(G\)就是非连通的, 因而, 规定其边连通度 \[{\lambda}(G)=0.\]

例: 如图所示,

点连通度\[{\chi}(G)=1,\] 边连通度\[{\lambda}(G)=2.\]

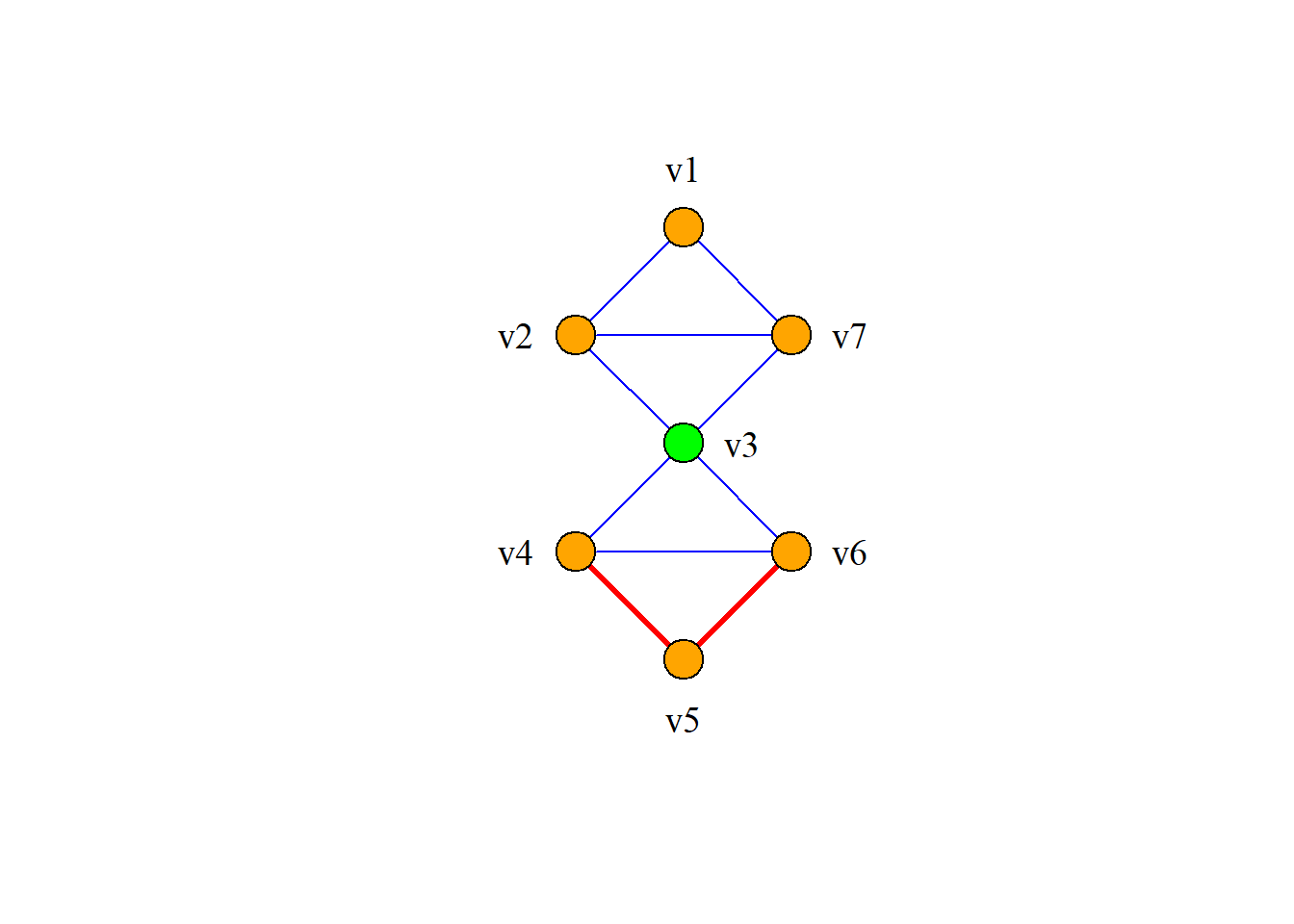
定理: 对于任何无向图, 有 \[{\chi}(G){\leq}{\lambda}(G){\leq}{\delta}(G)\] 例: 如图所示,

该图的点连通度\[{\chi}(G)=1.\]

边连通度\[{\lambda}(G)=2.\]

最小度\[{\delta}(G)=2.\]

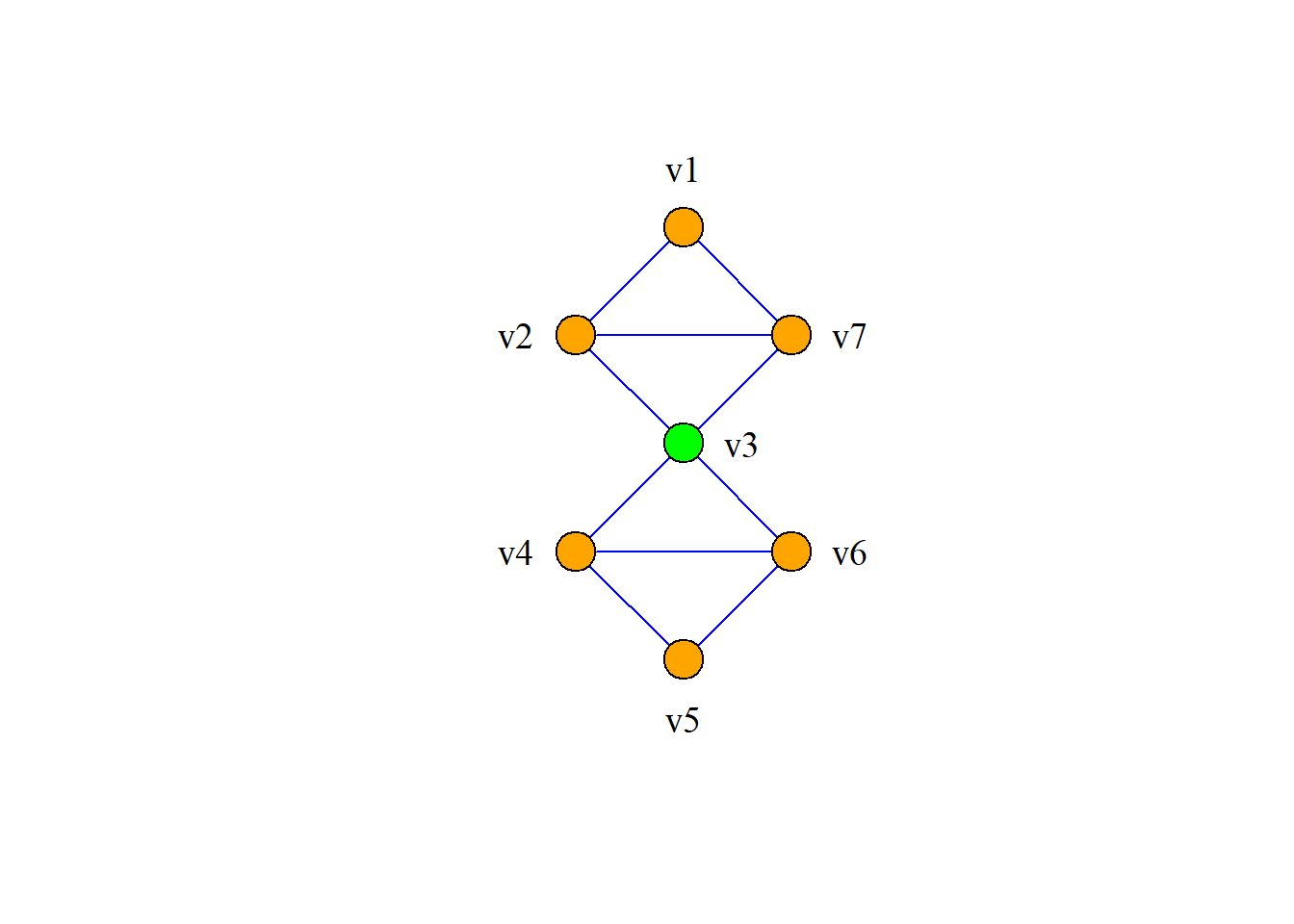
在任意6人的集会上, 总有3人互相认识, 或总有3人互相不认识. 如何证明？

3人相互认识即\(G\)包含\(K_3\)为子图;

3人相互不认识即\(G\)包含\({\langle}3, 0\rangle\)图为子图.

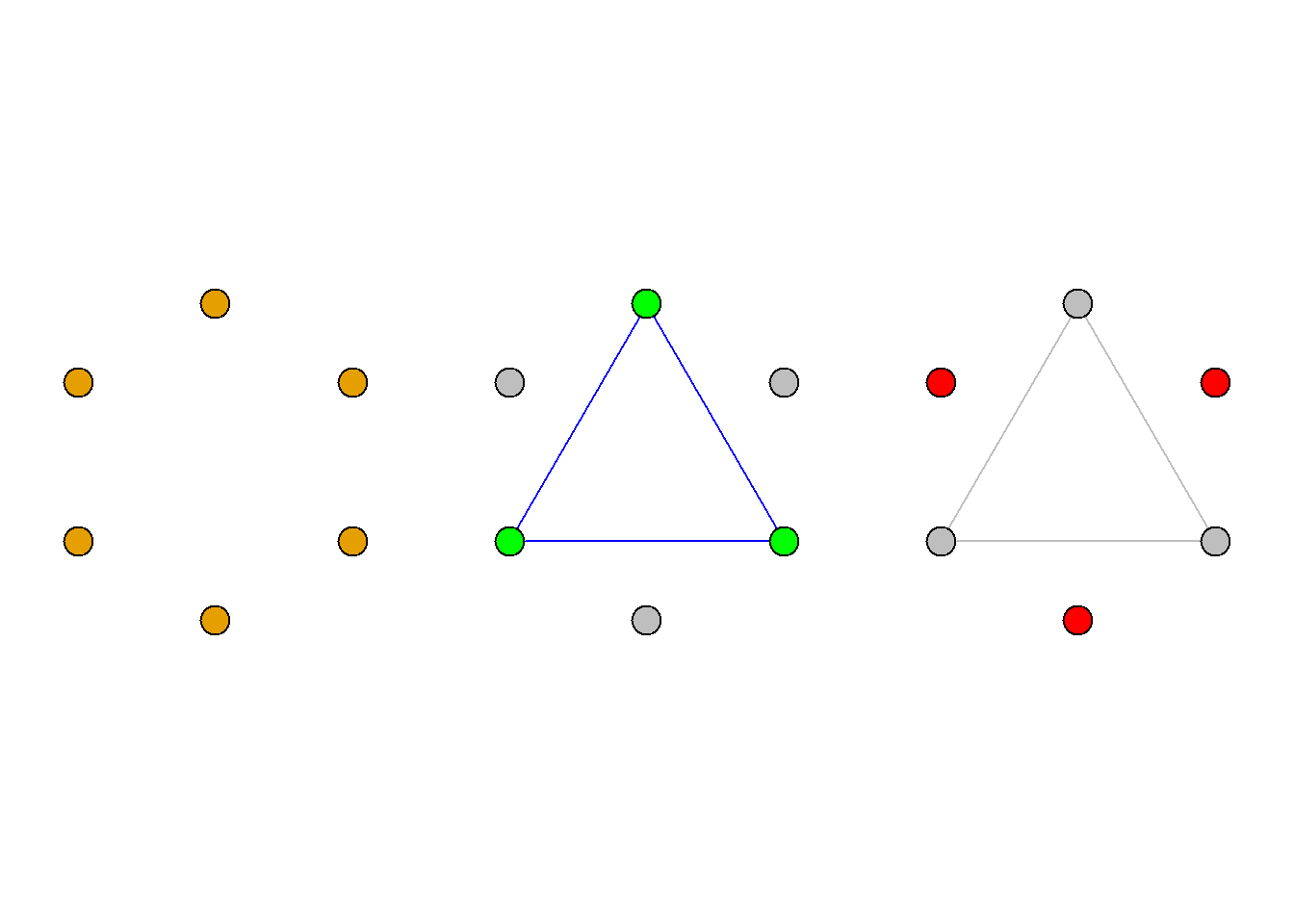
任取\(V\)中结点\(v\), 则有两种情况:

(1)\(v\)至少与另外3个结点邻接, 这又包含两种情况:

这三个结点互不邻接, 则\(G\)包含\({\langle}3, 0{\rangle}\)为子图;
这三个结点至少有两个邻接, 则\(G\)包含\(k_3\)为子图.

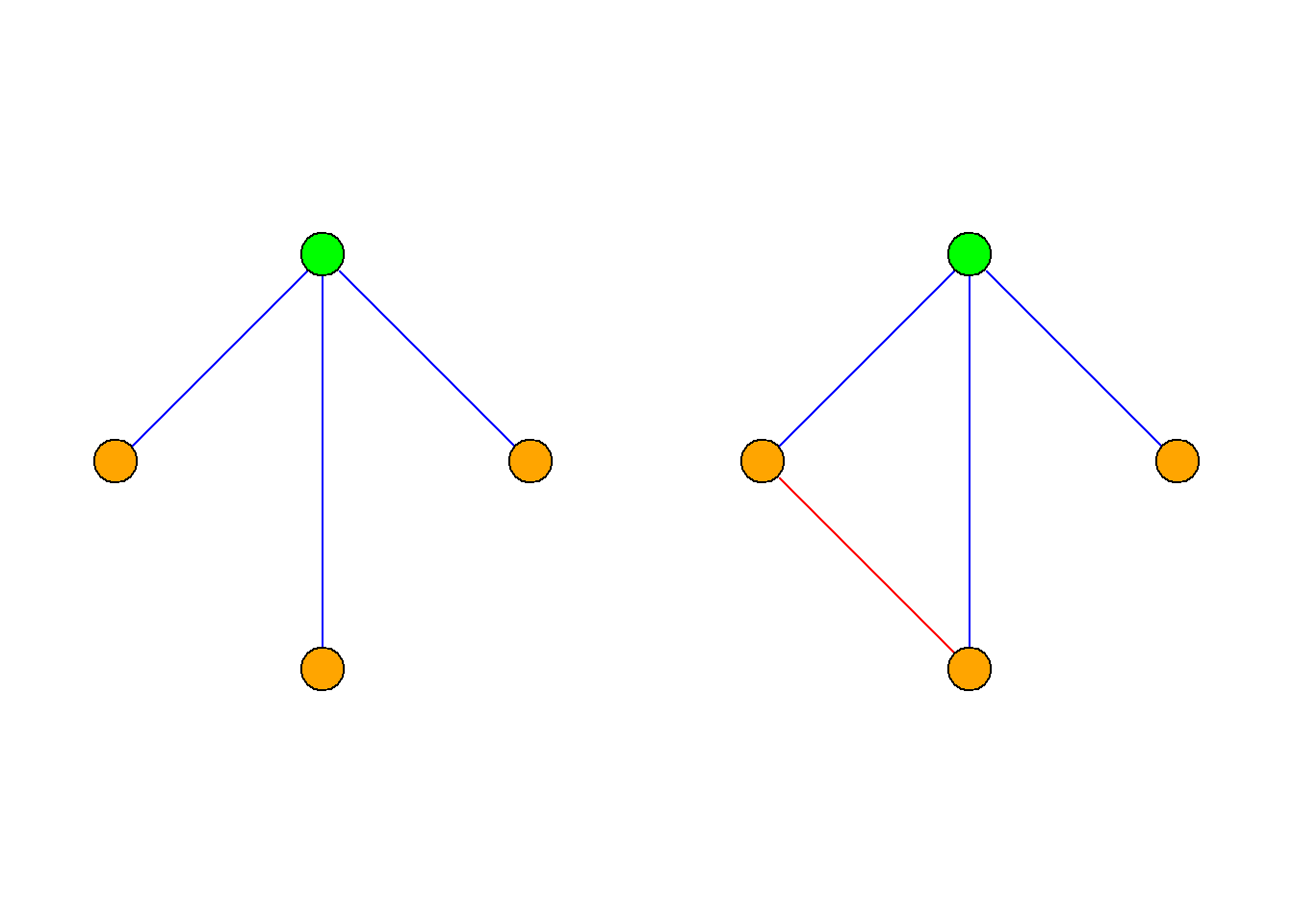
(2)\(v\)至多与另外2个结点邻接(即至少与另外3个结点不邻接), 这又包含两种情况:

这3个结点两两邻接, 则\(G\)包含\(k_3\)为子图.
这3个结点至少2结点不邻接, 则\(G\)包含\({\langle}3, 0{\rangle}\)为子图.

证明在任意一次集会中和奇数个人握手的人的个数为偶数个.

解: 将集会中的人作为结点, 若两个人握手则对应的结点连线, 则的简单图\(G\).

这样\(G\)中点\(v\)的度对应于集会中与\(v\)握手的人的个数.于是, 问题转化为证明“图\(G\)中度数为奇数的点的个数为偶数”.

根据定理“在任何图\(G={\langle}V, E{\rangle}\)中, 度为奇数的结点个数必为偶数”, 得证.

图的数学抽象是三元组, 其形象直观的表示即图的图示.

为便于计算, 图也可以用矩阵来表示, 图的结点和结点之间关系、结点与边之间关系、边与回路之间关系, 都可以用矩阵表示.

可以充分利用矩阵代数中的各种运算来研究图的结构特征及其性质, 这样便于用计算机处理图.

图的矩阵表示

任意图

关联矩阵定义: 设\(G={\langle}V, E{\rangle}\)是无向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), \(E=\{e_1, e_2, {\cdots}, e_m\}\), 设\(m_{ij}\)为结点\(v_i\)与边\(e_j\)的关联次数, 称\((m_{ij})_{n{\times}m}\)为\(G\)的关联矩阵, 记为\(M(G)\)或\(M\).

例: 无向图\(G\)如图所示, 其关联矩阵\(M\):

\[ \left( \begin{aligned} 1&1&1&0&0&0&0\\ 1&1&0&1&0&0&0\\ 0&0&0&1&2&1&0\\ 0&0&0&0&0&1&1\\ 0&0&1&0&0&0&1\\ \end{aligned} \right) \]

定义: 设\(G={\langle}V, E{\rangle}\)是有向无环图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), \(E=\{e_1, e_2, {\cdots}, e_m\}\), 则矩阵\(M(G)=(m_{ij})n{\times}m\)称为\(G\)的关联矩阵, 简记为\(M\). 其中: \[ m_{ij}= \begin{cases} 0 & 若e_j不关联v_i \\ 1 & 若v_i是e_j的始点 \\ -1 & 若v_i是e_j的终点 \\ \end{cases} \] 例: 给出有向图\(G\)如图所示, 其关联矩阵\(M\): \[\left( \begin{aligned} 1&1&-1&-1&0&0&0\\ -1&-1&0&0&1&0&0\\ 0&0&1&0&-1&1&0\\ 0&0&0&0&0&-1&-1\\ 0&0&0&1&0&0&1\\ \end{aligned} \right) \]

定义: 设\(G={\langle}V, E{\rangle}\)是无向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), 则\(n{\times}n\)阶矩阵\(A(G)=(a_{ij})n{\times}n\)称为\(G\)的邻接矩阵. 简记为\(A\). 其中: \(a_{ij}\)是同时以\(v_i\)和\(v_j\)为端点边数.

例: 给出无向图\(G\)如图所示, 它的邻接矩阵\(M\)为:

\[\left( \begin{aligned} 0&2&0&0&1\\ 2&0&1&0&0\\ 0&1&0&1&0\\ 0&0&1&0&1\\ 1&0&0&1&0\\ \end{aligned} \right) \] ’

定义: 设\(G={\langle}V, E{\rangle}\)是有向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), 则\(n{\times}n\)阶矩阵

\(A(G)=(a_{ij})_{n{\times}n}\)

称为\(G\)的邻接矩阵. 简记为\(A\). 其中: \(a_{ij}\)是\(v_i\)邻接到\(v_j\)的边数.

例: 给出有向图\(G\)如图所示, 它的邻接矩阵\(A\)为:

\[\left( \begin{aligned} 0&2&0&0&1\\ 0&0&1&0&0\\ 1&0&1&1&0\\ 0&0&0&0&0\\ 1&0&0&1&0\\ \end{aligned} \right) \]

简单图

定义: 设\(G={\langle}V, E{\rangle}\)是简单无向图, \(V=\{v_1, v_2, {\cdots}, v_n\},\,E=\{e_1, e_2, {\cdots}, e_m\}\), 矩阵\(M=(m_{ij})_{n{\times}m}\)称为\(G\)的关联矩阵, 其中:

\[ m_{ij}= \begin{cases} 1 & 若e_j关联v_i \\ 0 & 若e_j不关联v_i \\ \end{cases} \]

简单无向图的关联矩阵\(M\)具有以下特性:

矩阵的每一列恰有两个1, 因为每条边关联两个结点.
矩阵的每一行元素之和为对应结点的度.
若一行中元素全为0, 说明所对应的结点为孤立点.

例: 给出简单无向图\(G\)如图所示, 它的关联矩阵\(M\)为: \[\left( \begin{aligned} 1&0&1&0&1&0&1\\ 1&1&0&0&0&0&0\\ 0&1&1&1&0&0&0\\ 0&0&0&1&1&1&0\\ 0&0&0&0&0&1&1\\ \end{aligned} \right) \]

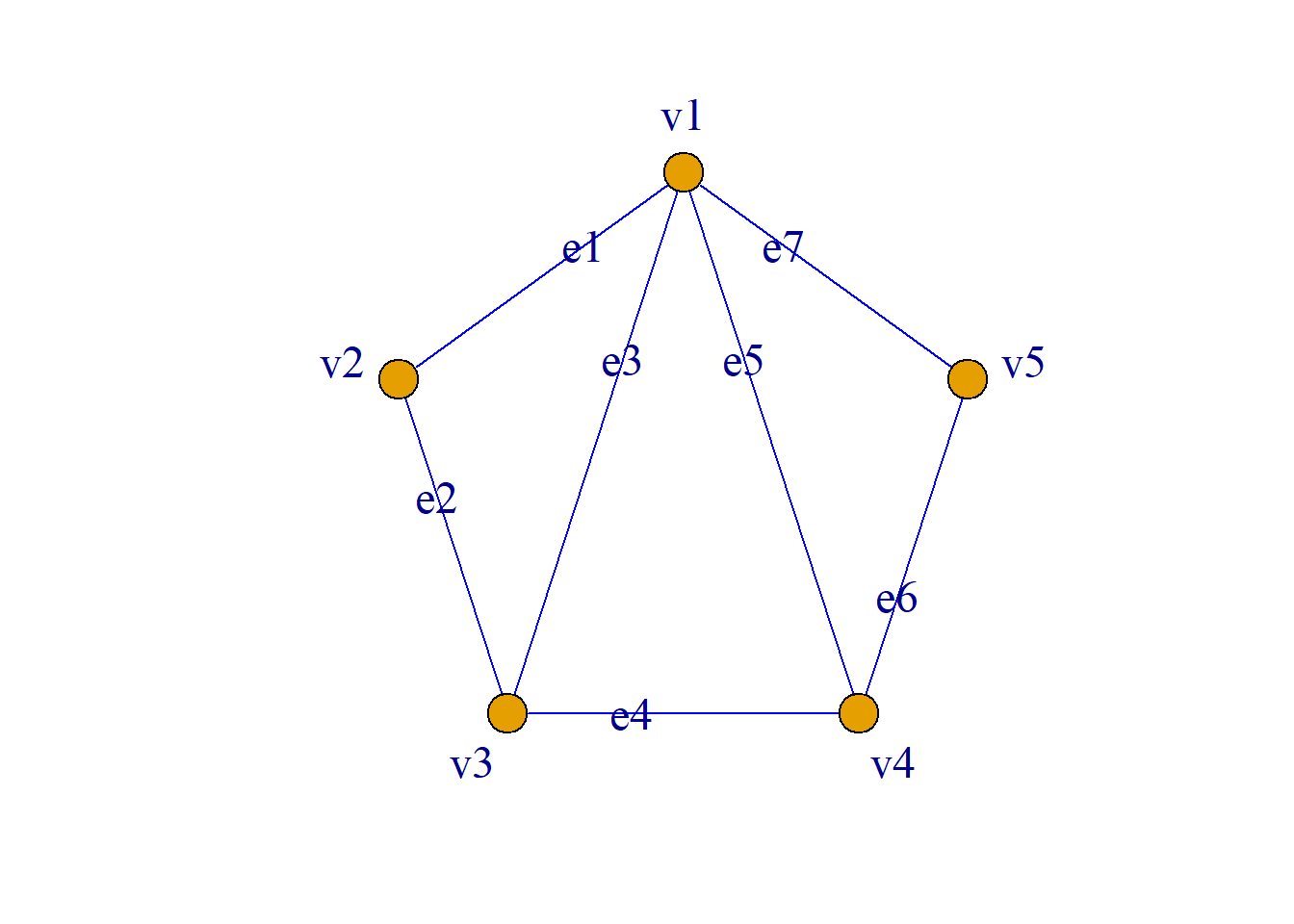
定义: 设\(G={\langle}V, E{\rangle}\)是简单有向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), \(E=\{e_1, e_2, {\cdots}, e_m\}\), 则矩阵\(M=(m_{ij})_{n{\times}m}\)称为\(G\)的关联矩阵, 其中: \[ m_{ij}= \begin{cases} 0 & 若e_j不关联v_i \\ 1 & 若v_i是e_j的始点 \\ -1 & 若v_i是e_j的终点 \\ \end{cases} \]

简单有向图的关联矩阵\(M\)具有以下特性:

矩阵的每一列元素之和为0, 因为每条边关联两个结点, 一个是它的始点, 一个是它的终点.
矩阵的每一行元素绝对值之和为对应结点的度.
矩阵的所有元素的代数和为0.

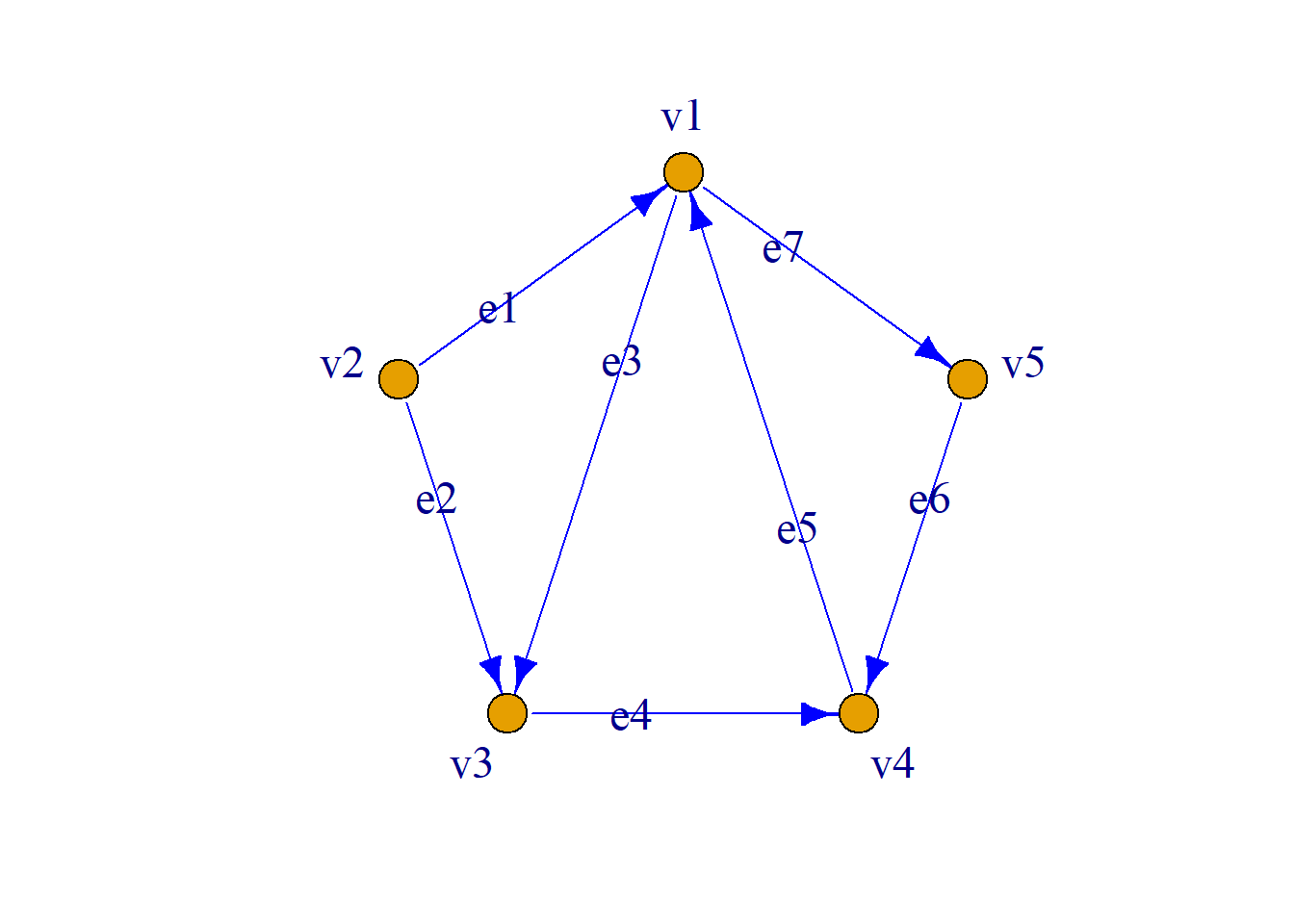
例: 给出简单有向图\(G\)如图所示, 它的关联矩阵\(M\)为:

\[\left( \begin{aligned} -1&0&1&0&-1&0&1\\ 1&1&0&0&0&0&0\\ 0&-1&-1&1&0&0&0\\ 0&0&0&-1&1&-1&0\\ 0&0&0&0&0&1&-1\\ \end{aligned} \right) \]

定义: 设\(G={\langle}V, E{\rangle}\)是简单无向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\) 则\(n{\times}n\)阶矩阵\(A=(a_{ij})_{n{\times}n}\)称为\(G\)的邻接矩阵, 其中:

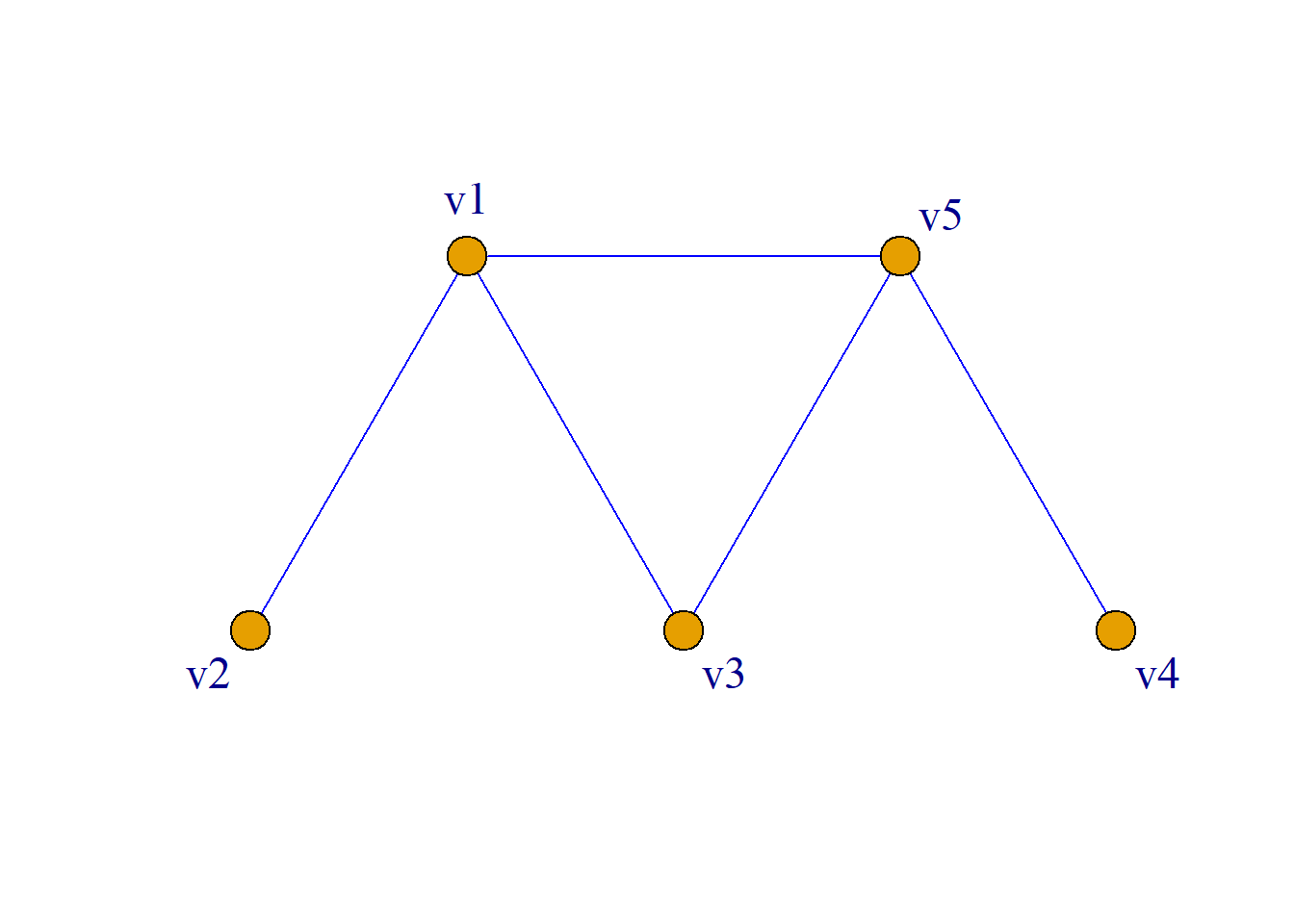
\[ a_{ij}= \begin{cases} 1 & 若(v_i, v_j){\in}E \\ 0 & 若(v_i, v_j){\notin}E \\ \end{cases} \] 例: 简单无向图\(G\)的邻接矩阵为: \[\left( \begin{aligned} 0&1&1&0&1\\ 1&0&0&0&0\\ 1&0&0&0&1\\ 0&0&0&0&1\\ 1&0&1&1&0\\ \end{aligned} \right) \]

定义: 设\(G={\langle}V, E{\rangle}\)是简单有向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), 则\(n{\times}n\)阶矩阵\(A=(a_{ij})_{n{\times}n}\)称为\(G\)的邻接矩阵, 其中:

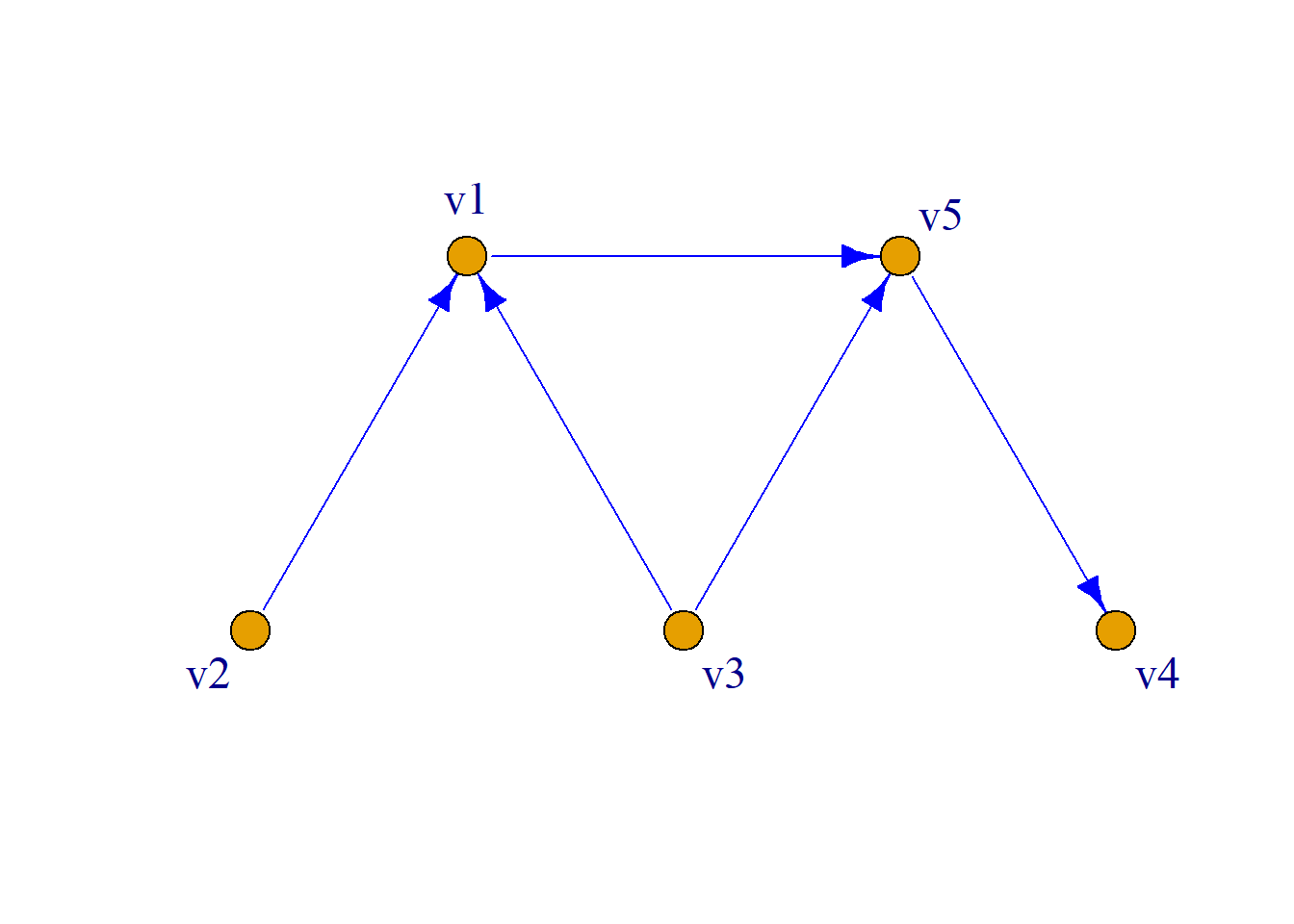
\[ a_{ij}= \begin{cases} 1 & 若{\langle}v_i, v_j{\rangle}{\in}E \\ 0 & 若{\langle}v_i, v_j{\rangle}{\notin}E \\ \end{cases} \] 例: 简单有向图\(G\)的邻接矩阵为:

\[\left( \begin{aligned} 0&0&0&0&1\\ 1&0&0&0&0\\ 1&0&0&0&1\\ 0&0&0&0&0\\ 0&0&0&1&0\\ \end{aligned} \right) \]

简单无向图的邻接矩阵是对称矩阵; 简单有向图的邻接矩阵未必是对称矩阵.

由邻接矩阵的定义可知, 一个图的邻接矩阵依赖于结点的标定顺序, 不同的结点顺序产生不同的邻接矩阵.

但两个不同的结点顺序得到的邻接矩阵密切相关, 只要简单地互换某些行及相应的列就可以从一个邻接矩阵得到另一个邻接矩阵.

\(G_1\)和\(G_2\)的邻接矩阵分别为:

\[\left( \begin{aligned} 0&0&0&1\\ 1&0&0&0\\ 1&0&0&1\\ 0&0&0&0\\ \end{aligned} \right) \] \[ \left( \begin{aligned} 0&1&0&0\\ 0&0&0&1\\ 0&1&0&1\\ 0&0&0&0\\ \end{aligned} \right) \] 交换1、2行和1、2列.

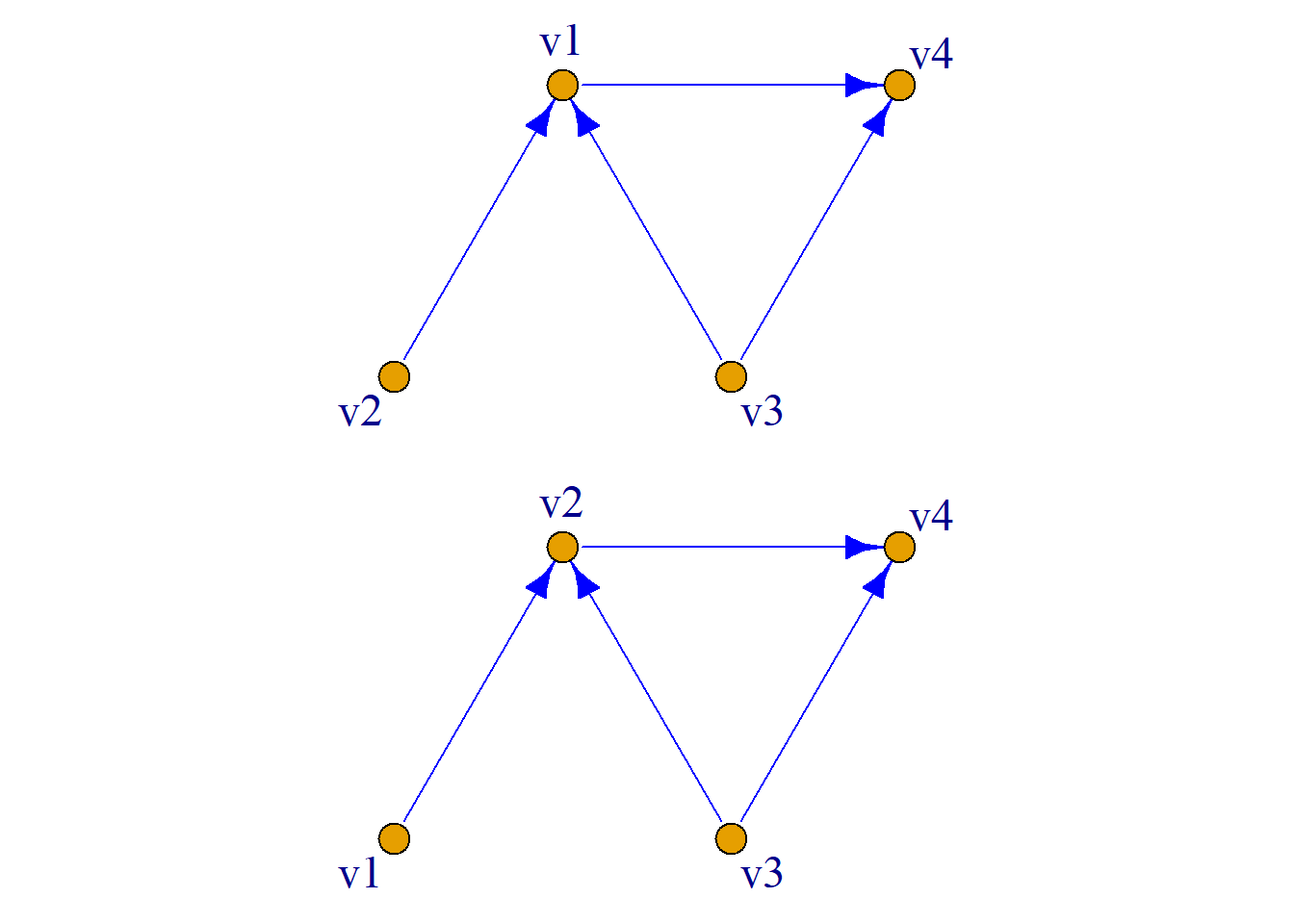
由于\(n\)个结点有\(n!\)个不同的顺序, 所以含有\(n\)个结点的图有\(n!\)个不同的邻接矩阵.

一般总是固定图\(G\)中结点的顺序, 以使其邻接矩阵唯一.

每一个简单图都对应这样一个布尔矩阵. 反之, 一个主对角线元素全为0的布尔矩阵也唯一地定义了一个简单图.

\[ \left( \begin{aligned} 0&1&1&1\\ 1&0&0&0\\ 1&0&0&1\\ 1&0&1&0\\ \end{aligned} \right) \]

邻接矩阵反映了简单图的一些基本性质:若一个邻接矩阵中, 除主对角线元素全为0外, 其余元素均为1, 则它所对应的图是完全图.

\[ \left( \begin{aligned} 0&1&1&1\\ 1&0&1&1\\ 1&1&0&1\\ 1&1&1&0\\ \end{aligned} \right) \]

若一个邻接矩阵是零矩阵, 则它所对应的图是零图

\[ \left( \begin{aligned} 0&0&0\\ 0&0&0\\ 0&0&0\\ \end{aligned} \right) \]

此外, 还可通过对邻接矩阵的某些运算来得到对应图的一些数量特性.

设简单有向图\(G={\langle}V, E{\rangle}\)的邻接矩阵为 \(A=(a_{ij})_{n{\times}n}\), \(A^T\)为\(A\)的转置矩阵, 定义\(B=(b_{ij})_{n{\times}n}\), \(C=(c_{ij})_{n{\times}n}\), 其中 \(B=A{\times}A^T\), \(C=A^T{\times}A\). \({\times}\)为矩阵乘法.

矩阵\(A\)中, 第\(i\)行中值为1的元素数目等于结点\(v_i\)的出度; 第\(i\)列中值为1的元素数目等于结点\(v_i\)的入度; 第\(i\)行中值为1的元素数目与第\(i\)列中值为1的元素数目之和等于结点\(v_i\)的度.

即: \[d^+(v_i)=\sum_{k=1}^na_{ik}, \,\,d^-(v_i)=\sum_{k=1}^na_{ki}, \,\,d(v_i)=\sum_{k=1}^n(a_{ki}+a_{ik}).\]

对于矩阵\(B=A{\times}A^T\), 第\(i\)行第\(j\)列元素\(b_{ij}\):

\[b_{ij}=\sum_{k=1}^na_{ik}a_{jk}\]

意义是它表示分别从\(v_i\)和\(v_j\)出发的边有共同终点的那些终点的数目.

特别地, 主对角线元素\(b_{ii}\)就是结点\(v_i\)的出度.

对于矩阵\(C=A^T{\times}A\), 第\(i\)行第\(j\)列元素\(c_{ij}\): \[c_{ij}=\sum_{k=1}^na_{ki}a_{kj}\] 意义是从共同始点出发的边终止于\(v_i\)和\(v_j\)的那些始点的数目.特别地, 主对角线元素\(c_{ii}\)就是结点\(v_i\)的入度.

例:

\[A= \left( \begin{aligned} 0&0&0&1\\ 1&0&0&0\\ 1&1&0&1\\ 1&1&1&0\\ \end{aligned} \right) \]

在矩阵\(A\)中, 第4行值为1的元素数目为3, 而图中结点\(v_4\)的出度正是3; 第2列值为1的元素数目为2, 而图中结点\(v_2\)的入度正是2; 第3行中值为1的元素数目与第3列中值为1的元素数目之和为4, 而图中结点\(v_3\)的度正是4.

又: \(B=A{\times}A^T=\)

\[ \left( \begin{aligned} 0&0&0&1\\ 1&0&0&0\\ 1&1&0&1\\ 1&1&1&0\\ \end{aligned} \right) \left( \begin{aligned} 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 1&0&1&0\\ \end{aligned} \right) \] \[ B=\left( \begin{aligned} 1&0&1&0\\ 0&1&1&1\\ 1&1&3&2\\ 0&1&2&3\\ \end{aligned} \right) \]

b₃₄=2, 而图中正有两个结点v₁和v₂, 使得分别从v₃和v₄出发的边都以它们为共同的终点;b₄₄=3, 而结点v₄的出度恰为3.

再有:

\(C=A^T{\times}A=\)

\[ \left( \begin{aligned} 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 1&0&1&1\\ \end{aligned} \right) \left( \begin{aligned} 0&0&0&1\\ 1&0&0&0\\ 1&1&0&1\\ 1&1&1&0\\ \end{aligned} \right) \] \[ C=\left( \begin{aligned} 3&2&1&1\\ 2&2&1&1\\ 1&1&1&0\\ 1&1&0&2\\ \end{aligned} \right) \]

c₃₁=1, 而图中正有一个结点v₄, 使得从v₄出发的边终止于v₃和v₁;c₂₂=2, 而结点的入度恰为2.

定理: 设\(A=(a_{ij})_{n{\times}n}\)为简单有向图\(G={\langle}V, E{\rangle}\)的邻接矩阵, \(A^l=(a_{ij}^{(l)})_{n{\times}n}\)为\(l\)个矩阵\(A\)的乘积, 则:

\(A^l\)的第\(i\)行第\(j\)列元素\(a_{ij}^{(l)}\)恰为结点\(v_i\)到\(v_j\)长度为\(l\)的通路数目.特别地, 第\(i\)行第\(i\)列元素\(a_{ii}^{(l)}\)恰为结点\(v_i\)到\(v_i\)长度为\(l\)的回路数;
\(A^l\)的全部元素之和恰是\(G\)中长度为\(l\)的通路数;
\(B_r=(b_{ij}^{(r)})_{n{\times}n}=A+A^2+{\cdots}+A^r\) 中, \(b_{ij}^{(r)}\)恰为结点\(v_i\)到\(v_j\)长度小于等于\(r\)的通路数目;
\(B_r\)的全部元素之和为\(G\)中长度小于等于\(r\)的通路数.

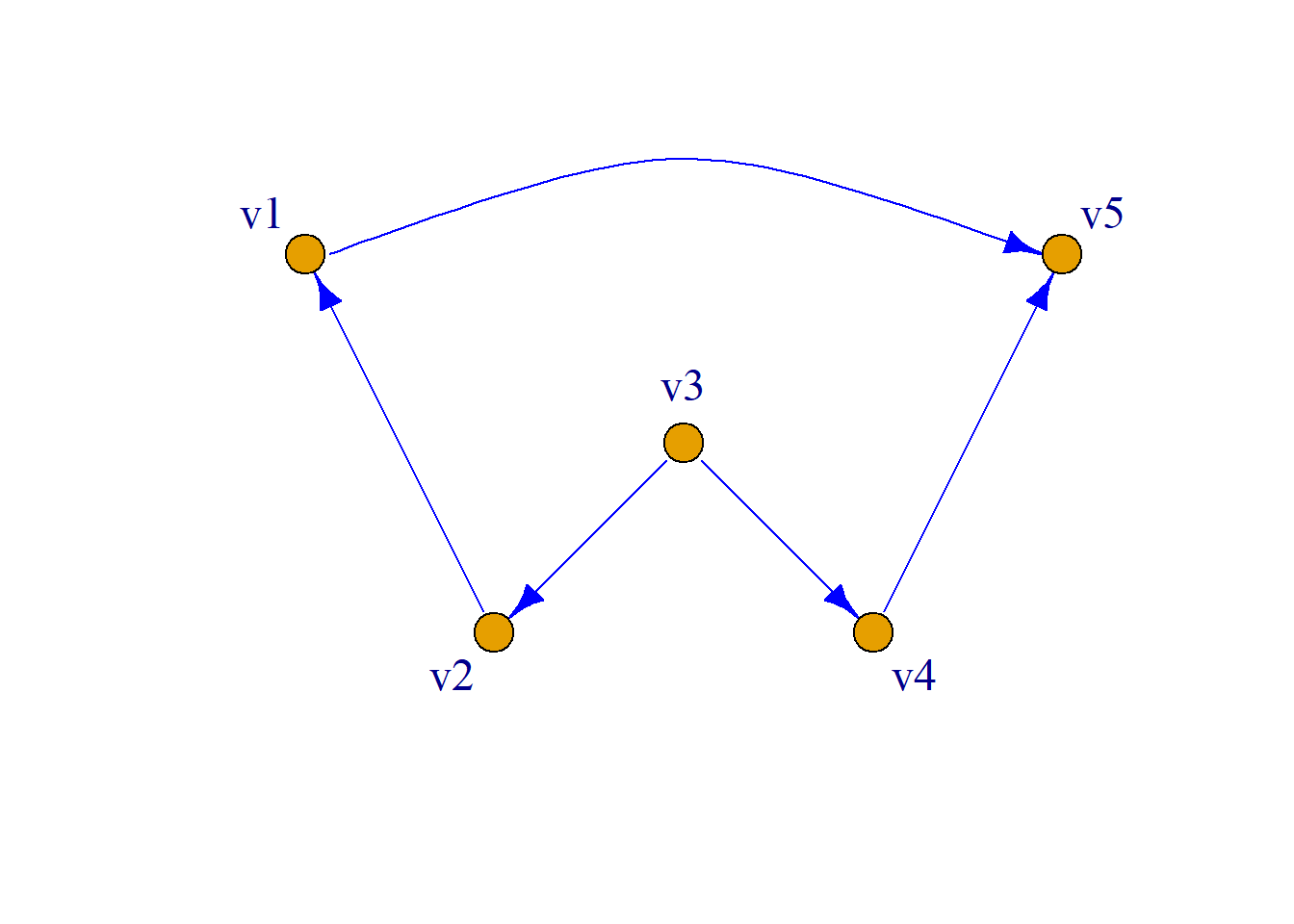
例: 给出简单有向图\(G\)如图所示, 它的邻接矩阵为 \[ \left( \begin{aligned} 0&1&0&0\\ 0&0&1&1\\ 1&1&0&1\\ 1&0&0&0\\ \end{aligned} \right) \]

\[\sum_{i=1}^4\sum_{j=1}^4a_{ij}=7, \sum_{i=1}^4a_{ii}=0\] 图中, \(a_{23}=1\), 说明从\(v_2\)到\(v_3\)有长度为1的路径1条; \(a_{42}=0\), 说明从\(v_4\)到\(v_2\)没有长度为1的路径; \(A\)中元素之和为7, 说明\(G\)中有7条长度为1的路径; \(A\)的对角线元素均为0, 说明\(G\)中无长度为1的回路.

\[ A^2=\left( \begin{aligned} 0&0&1&1\\ 2&\boxed{1}&0&1\\ 1&1&1&1\\ 0&1&0&0\\ \end{aligned} \right) \] \[ A^3= \left( \begin{aligned} 2&1&0&1\\ 1&2&\boxed{1}&1\\ 2&2&1&2\\ 0&\boxed{0}&1&1\\ \end{aligned} \right) \] \(a_{23}^3=1\)说明从\(v_2\)到\(v_3\)有1条长度为3的路径; \(a_{42} ^3=0\)说明从\(v_4\)到\(v_2\)没有长度为3的路径; \(a_{22}^2=1\)说明从\(v_2\)到\(v_2\)有1条长度为2的回路.

\[ B_4=\sum_{i=1}^4A^i= \left( \begin{aligned} 3&4&2&3\\ 5&{5}&4&6\\ 7&7&\boxed{4}&7\\ 3&\boxed{2}&1&2\\ \end{aligned} \right) \]

\(v_4\)到\(v_2\)长度不超过4的通路共有2条; \(v_3\)到\(v_3\)长度不超过4的回路共有4条.

定义: 设\(G={\langle}V, E{\rangle}\)是简单有向图, \(V=\{v_1, v_2, {\cdots}, v_n\}\), 则\(n{\times}n\)阶矩阵\(p=(p_{ij})_{n{\times}n}\)称为\(G\)的可达矩阵, 其中:

\[ p_{ij}= \begin{cases} 1 & 若v_i到v_j可达 \\ 0 & 若v_i到v_j不可达 \\ \end{cases} \]

可达矩阵: \[P= \left( \begin{aligned} 1&0&0&0&1\\ 1&1&0&0&1\\ 1&1&1&1&1\\ 0&0&0&1&1\\ 0&0&0&0&1\\ \end{aligned} \right) \]

由邻接矩阵\(A\)求得可达矩阵\(P\)的算法: 求矩阵: \[B_{n-1}=(b_{ij}^{(n-1)})_{n{\times}n}=A+A^2+{\cdots}+A^{n-1}\] 可由矩阵\(B_{n-1}\)求得可达矩阵\(P=(p_{ij})_{n{\times}n}\). \[ p_{ij}= \begin{cases} 1 & i=j \\ 1 & i{\neq}j, b_{ij}^{(n-1)}{\neq}0 \\ 0 & i{\neq}j, b_{ij}^{(n-1)}=0 \\ \end{cases} \]

因每个结点到自身总是可达的, 故定义对角线元素\(p_{ii}=1\)(\(i=1, 2, {\cdots}, n\)).

\[A= \left( \begin{aligned} 0&0&0&0&1\\ 1&0&0&0&0\\ 0&1&0&1&0\\ 0&0&0&0&1\\ 0&0&0&0&0\\ \end{aligned} \right) \] \[ A^2= \left( \begin{aligned} 0&0&0&0&0\\ 0&0&0&0&1\\ 1&0&0&0&1\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{aligned} \right) \]

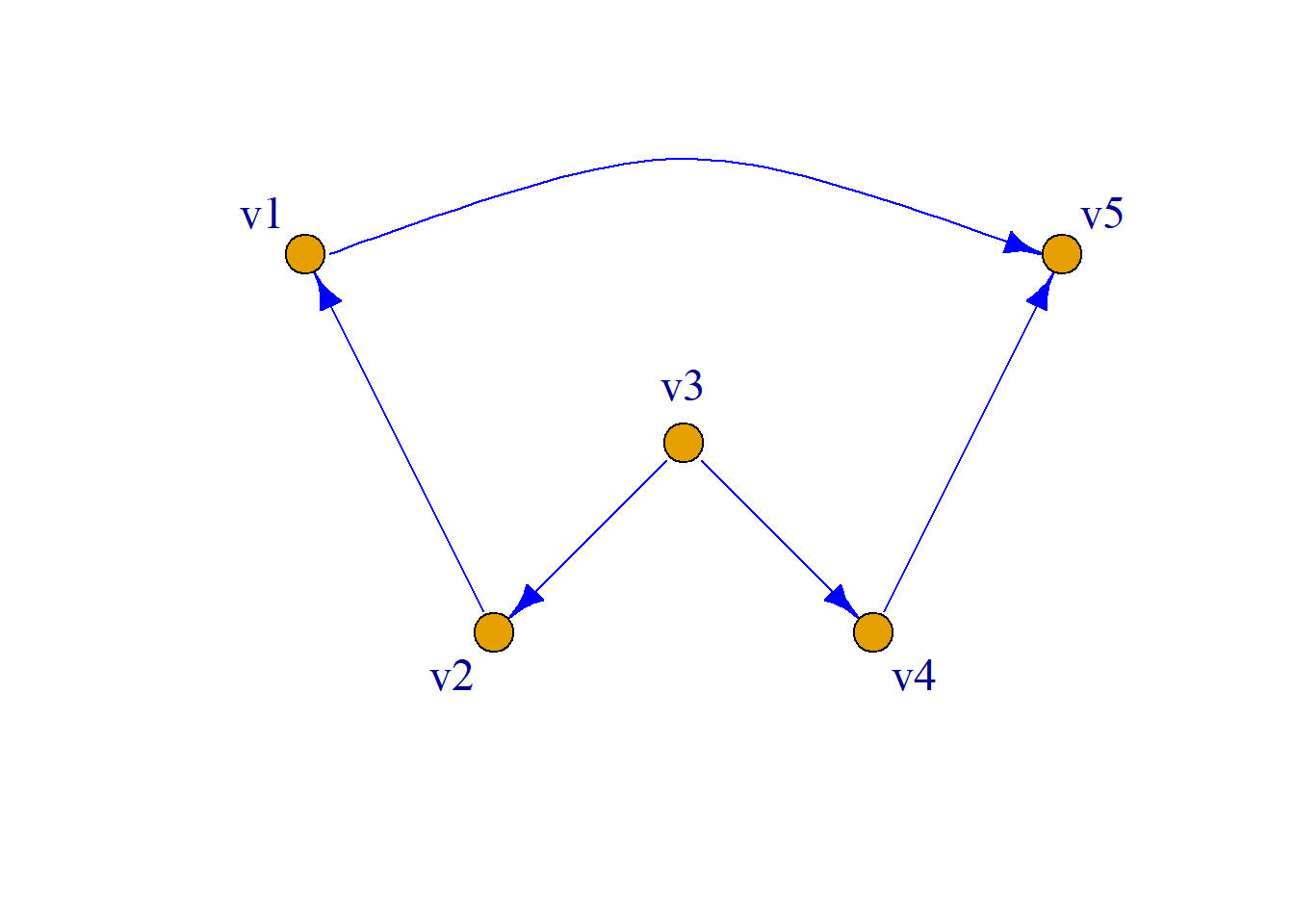
\[A^3= \left( \begin{aligned} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&1\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{aligned} \right) \] \[ A^4= \left( \begin{aligned} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{aligned} \right) \]

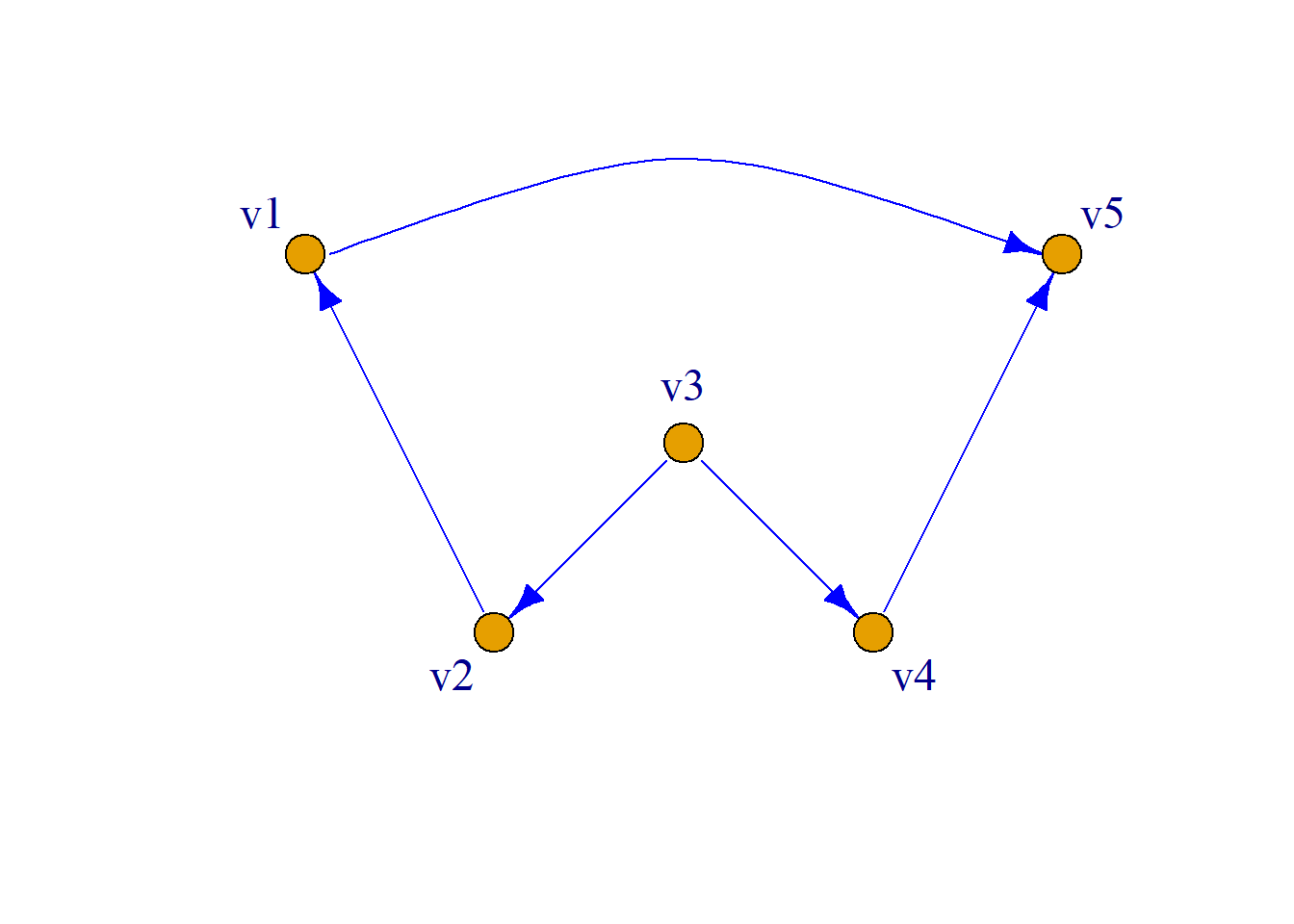
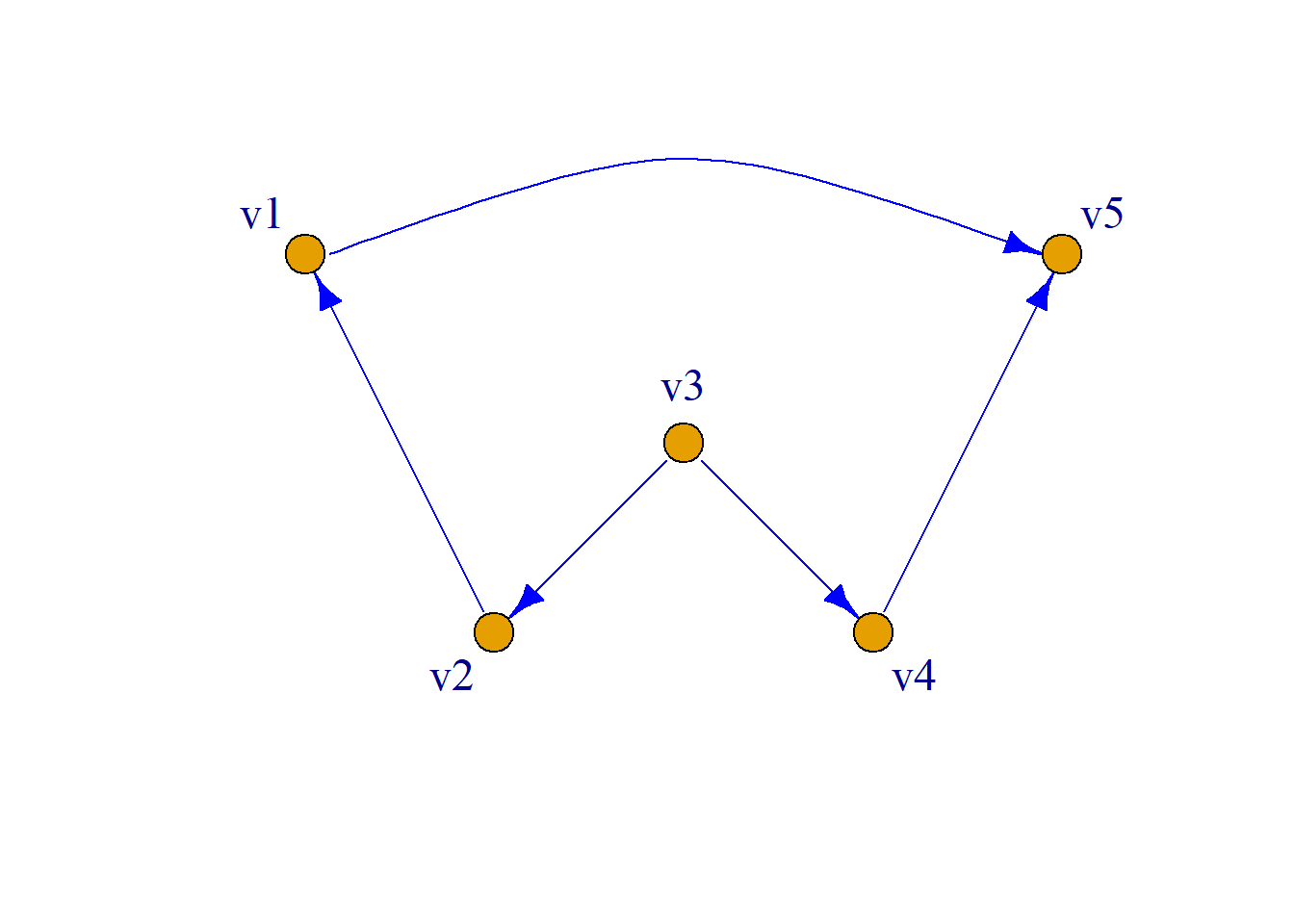
\[B_4=\sum{A^i}= \left( \begin{aligned} 0&0&0&0&1\\ 1&0&0&0&1\\ 1&1&0&1&2\\ 0&0&0&0&1\\ 0&0&0&0&0\\ \end{aligned} \right) \] 于是: \[P= \left( \begin{aligned} 1&0&0&0&1\\ 1&1&0&0&1\\ 1&1&1&1&1\\ 0&0&0&1&1\\ 0&0&0&0&1\\ \end{aligned} \right) \]

可以借助布尔矩阵求可达矩阵与强分图.

布尔运算是只涉及数字0和1的运算, 这些数字的并和交按下列方式进行: \[0{\vee}0=0, \, 0{\vee}1=1,\,1{\vee}0=1, \, 1{\vee}1=1\] \[0{\wedge}0=0, \, 0{\wedge}1=0,\,1{\wedge}0=0, \, 1{\wedge}1=1\] \({\vee}\)称为布尔并, \({\wedge}\)称为布尔交.

布尔矩阵的运算: 设\(B=(b_{ij})_{n{\times}n}\)和\(C=(c_{ij})_{n{\times}n}\)为布尔矩阵, 则两矩阵布尔并\(B{\vee}C\)、两矩阵的布尔交\(B{\wedge}C\)和两矩阵的布尔乘\(B{\cdot}C\)定义为: \[B{\vee}C=(b_{ij}{\vee}c_{ij})_{n{\times}n},\,\,B{\wedge}C=(b_{ij}{\wedge}c_{ij})_{n{\times}n},\,\,B{\cdot}C=(d_{ij})_{n{\times}n} \] 其中: \(d_{ij}=(b_{i1}{\wedge}c_{1j}){\vee}(b_{i2}{\wedge}c_{2j}){\vee}{\cdots}{\vee}(b_{in}{\wedge}c_{nj})\).

已知: \[ A=\left( \begin{aligned} 1&1&0\\ 0&1&0\\ 1&0&0\\ \end{aligned} \right) \, \, \, \, B=\left( \begin{aligned} 0&0&0\\ 1&1&0\\ 1&0&1\\ \end{aligned} \right) \]

则

\[ A{\vee}B=\left( \begin{aligned} 1&1&0\\ 1&1&0\\ 1&0&0\\ \end{aligned} \right) \, \, \, \, A{\wedge}B=\left( \begin{aligned} 0&0&0\\ 0&1&0\\ 1&0&1\\ \end{aligned} \right) \, \, \, \, A{\cdot}B=\left( \begin{aligned} 1&1&0\\ 1&1&0\\ 0&0&0\\ \end{aligned} \right) \]

设\(n\)个结点简单有向图的邻接矩阵为\(A\), 记: \[A^{2}=A{\cdot}A\] \[A^{3}=A^{2}{\cdot}A\] \[{\cdots}\] \[A^{l}=A^{l-1}{\cdot}A\]

则\(A\)的可达矩阵可表示为: \[P=I{\vee}A{\vee}A^{2}{\vee}{\cdots}{\vee}A^{n-1}\]

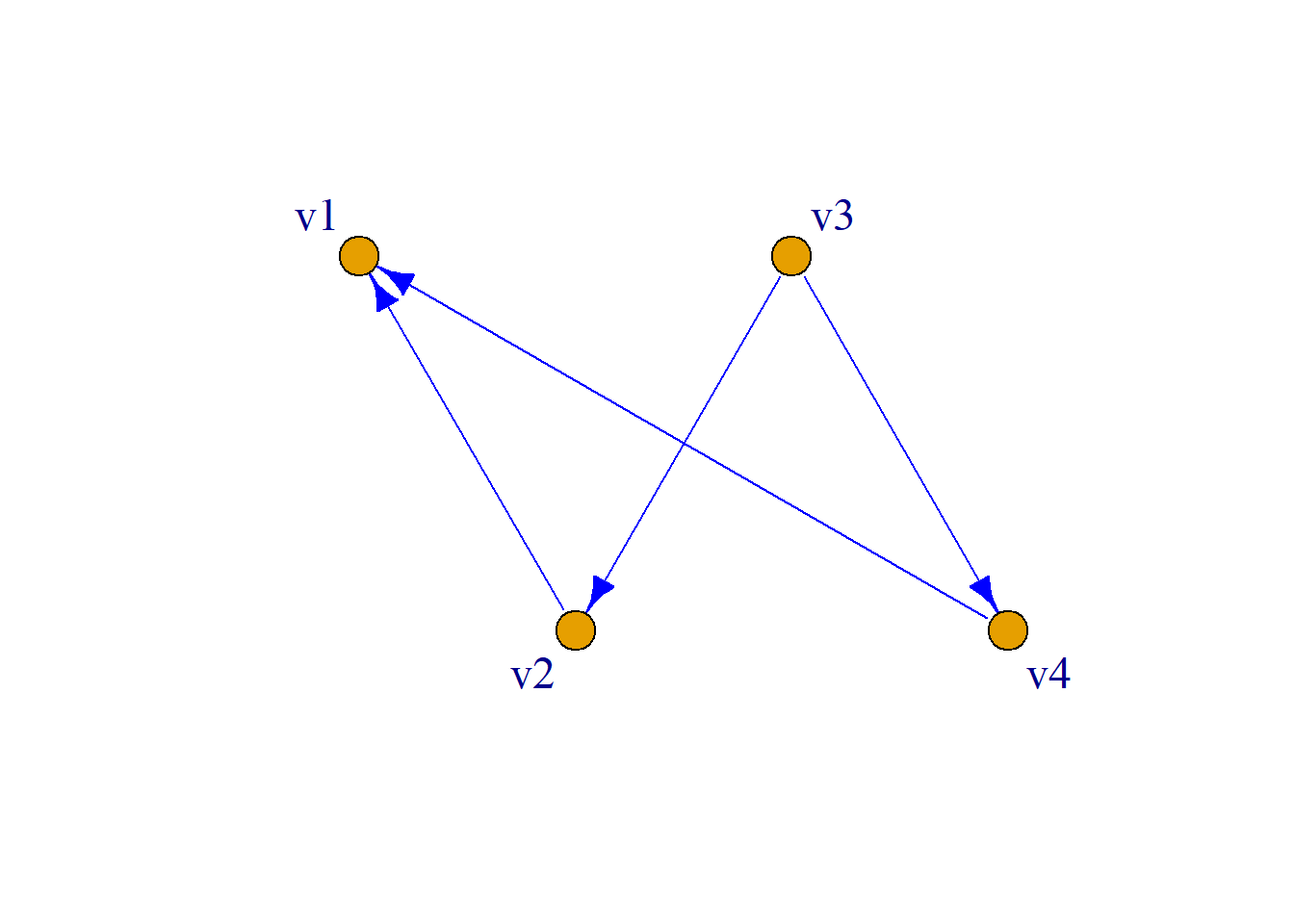
例: 简单有向图\(G\)如图, 求\(P\).

解: \(n=4\), \(n-1=3\)

\[ A= \left( \begin{aligned} 0&0&0&0\\ 1&0&0&0\\ 0&1&0&1\\ 1&0&0&0\\ \end{aligned} \right) \] \[P=I{\vee}A{\vee}A^2{\vee}A^3\]

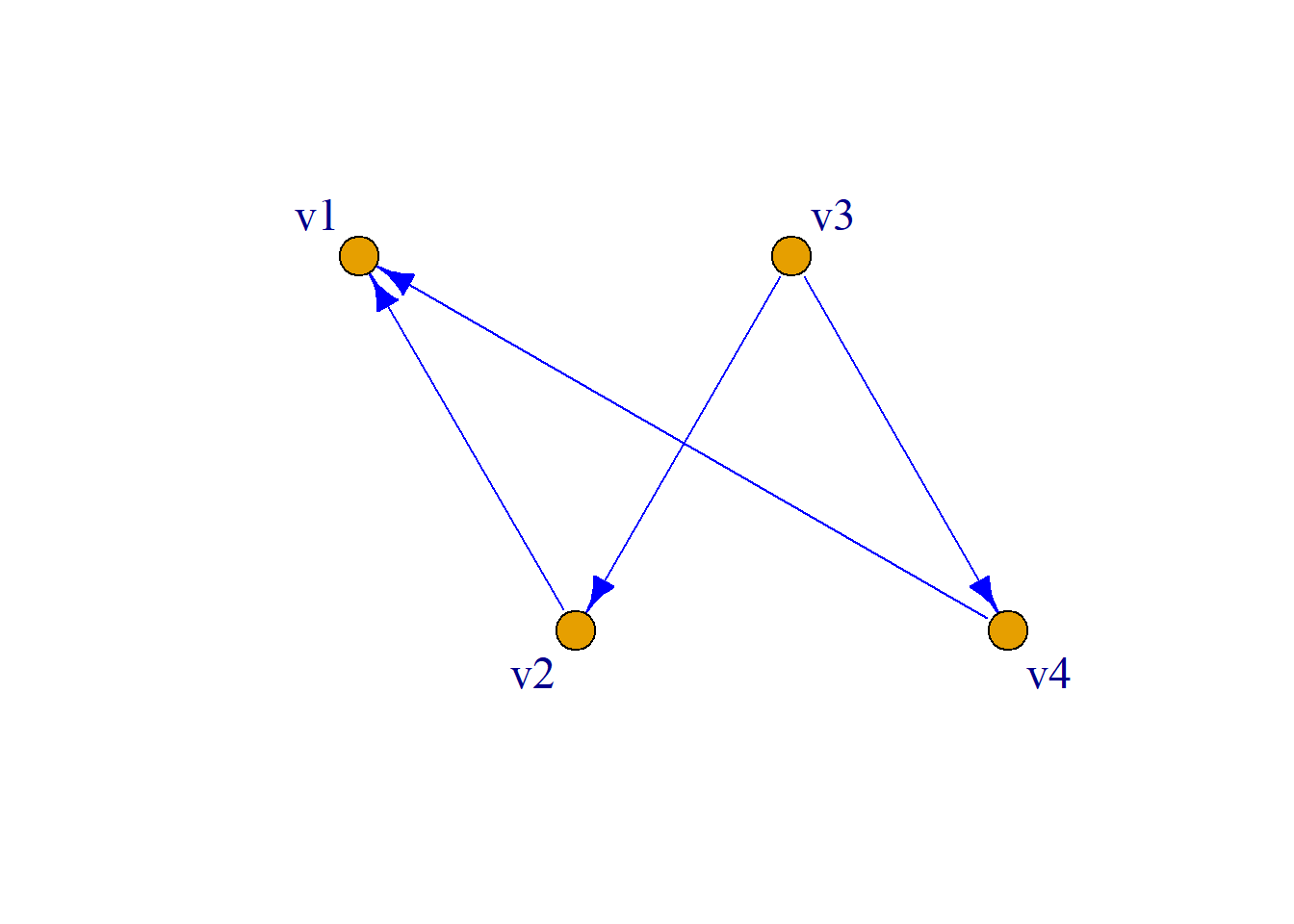
\[ A^2= \left( \begin{aligned} 0&0&0&0\\ 0&0&0&0\\ 1&0&0&0\\ 0&0&0&0\\ \end{aligned} \right) \, \, \, \, A^3={0} \]

\[ P= \left( \begin{aligned} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&1\\ 1&0&0&1\\ \end{aligned} \right) \]

对于简单有向图, 利用可达矩阵可求出图中包含任何指定结点的强分图.

算法:设\(G={\langle}V, E{\rangle}\)为简单有向图, \(P=(p_{ij})_{n{\times}n}\)为\(G\)的可达矩阵, \(P^T=(p_{ij})^T_{n{\times}n}\)为\(P\)的转置矩阵, 对于矩阵

\[P{\wedge}P^T=(p_{ij}{\wedge}p_{ji})_{n{\times}n}, \]

则其第\(i\)行非零元素对应的\(v_j\)与\(v_i\)构成含有\(v_i\)的强分图.

\[ P= \left( \begin{aligned} 1&1&1&0\\ 1&1&1&0\\ 1&1&1&0\\ 1&1&1&1\\ \end{aligned} \right) \] \[ P{\wedge}P^T= \left( \begin{aligned} 1&1&1&0\\ 1&1&1&0\\ 1&1&1&0\\ 0&0&0&1\\ \end{aligned} \right) \]

可知, \(G[\{v_1, v_2, v_3\}]\)和\(G[\{v_4\}]\)是强分图.