格和布尔代数

主讲教师

李辉

格

偏序集定义的格

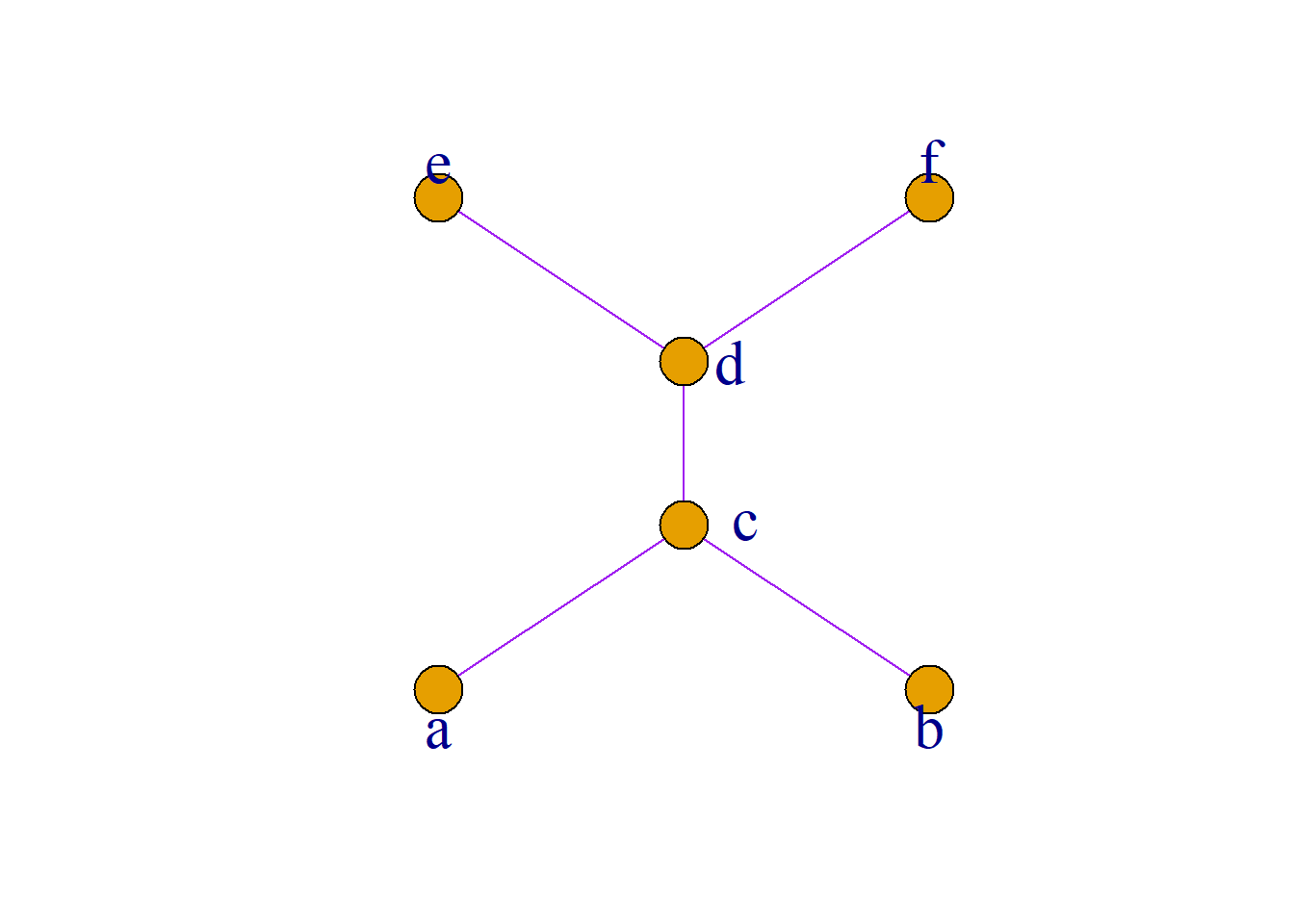
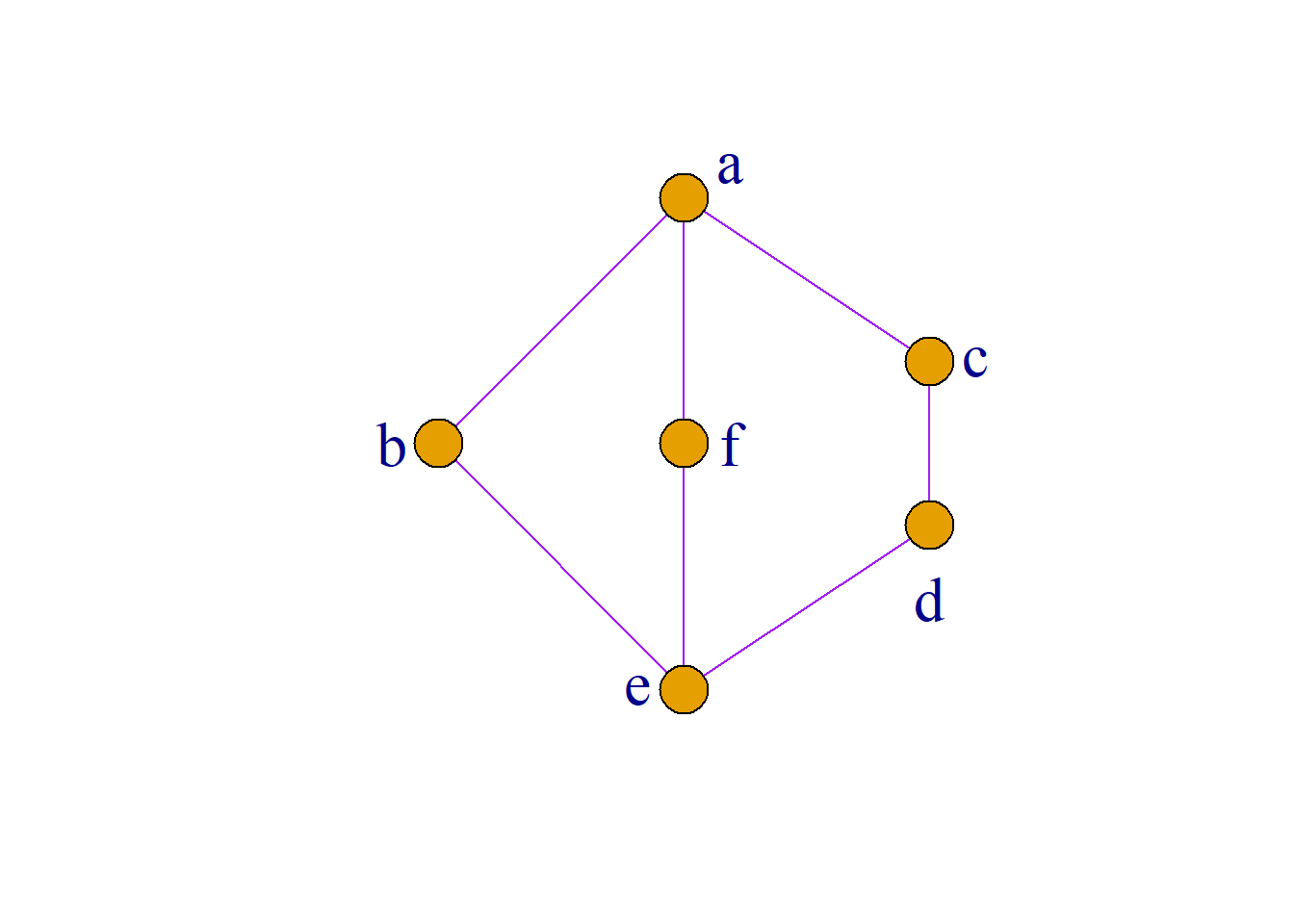
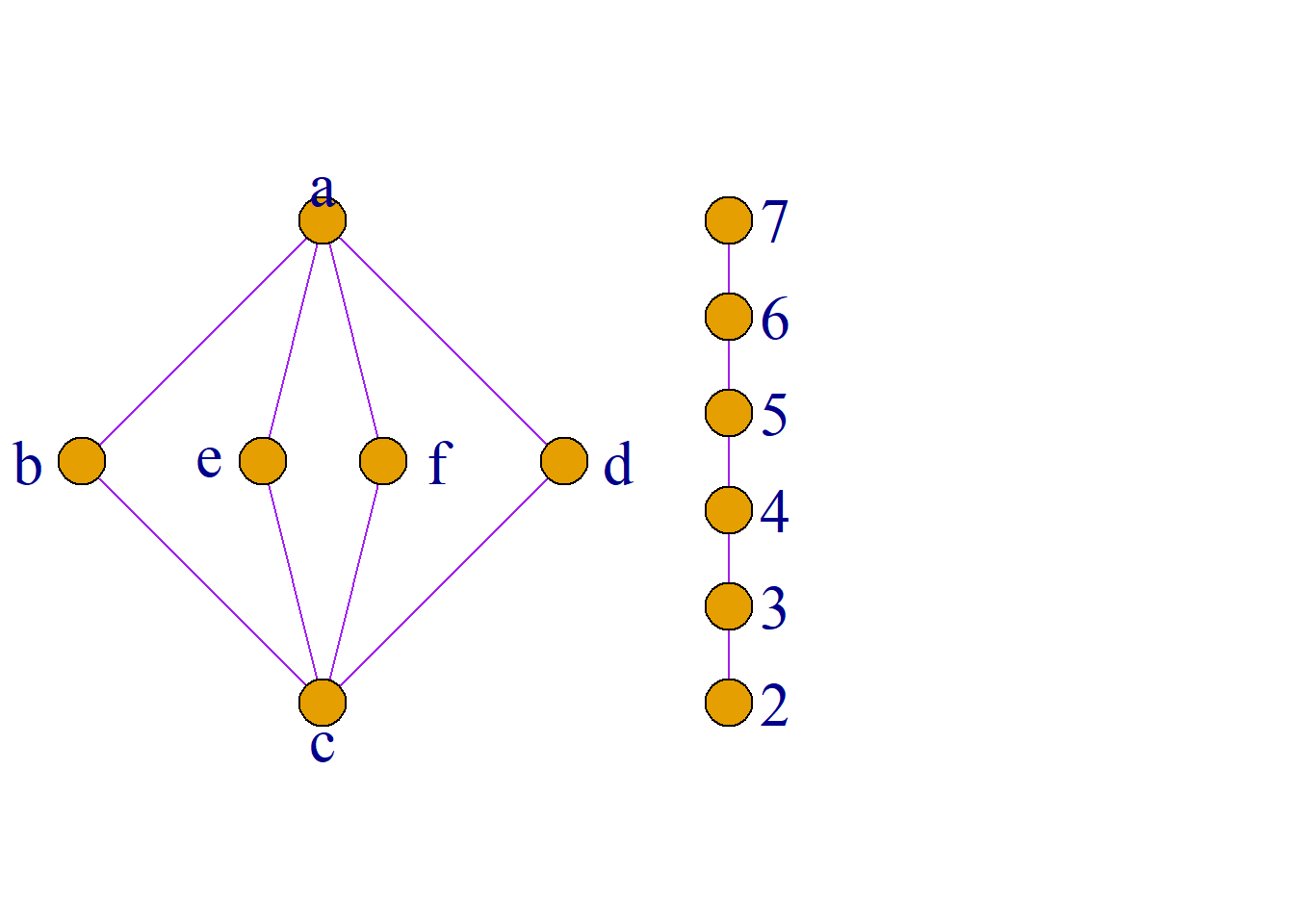
一个偏序集\({\langle}S, {\leq}{\rangle}\), 其任意子集\(T\)(\(T{\subseteq}S\))未必有最大下界和最小上界. 例如, 如图所示的偏序集.

\(S=\{a, b, c, d, e, f\}\)

\(T_1=\{a, b\}\)的最小上界\(c\), 没最大下界;

\(T_2=\{e, f\}\)没有最小上界.最大下界是\(d\);

\(T_3=\{c, d\}\)最小上界\(d\), 最大下界是\(c\).

接下来的偏序集则都有一个共同的性质.

就是在这个偏序集中, 任何两个元素都有最小上界和最大下界.

我们把具有这种性质的偏序集称为格.

定义: 设\({\langle}L, {\leq}{\rangle}\)是一个偏序集, 如果\(L\)中任意两个元素\(a\)和\(b\)都有最小上界和最大下界在L中存在, 则称\({\langle}L, {\leq}{\rangle}\)为格. 也称这样定义的格为偏序格.

一般用\(a{\vee}b\), \(LUB\{a, b\}\)或\(sup\{a, b\}\)表示\(a\)和\(b\)的最小上界(join 或 supremum). 用\(a{\wedge}b\), \(GLB\{a, b\}\)或\(inf\{a, b\}\)表示\(a\)和\(b\)的最大下界(meet 或 infimum), \({\vee}\)和\({\wedge}\)分别称为保联运算和保交运算.

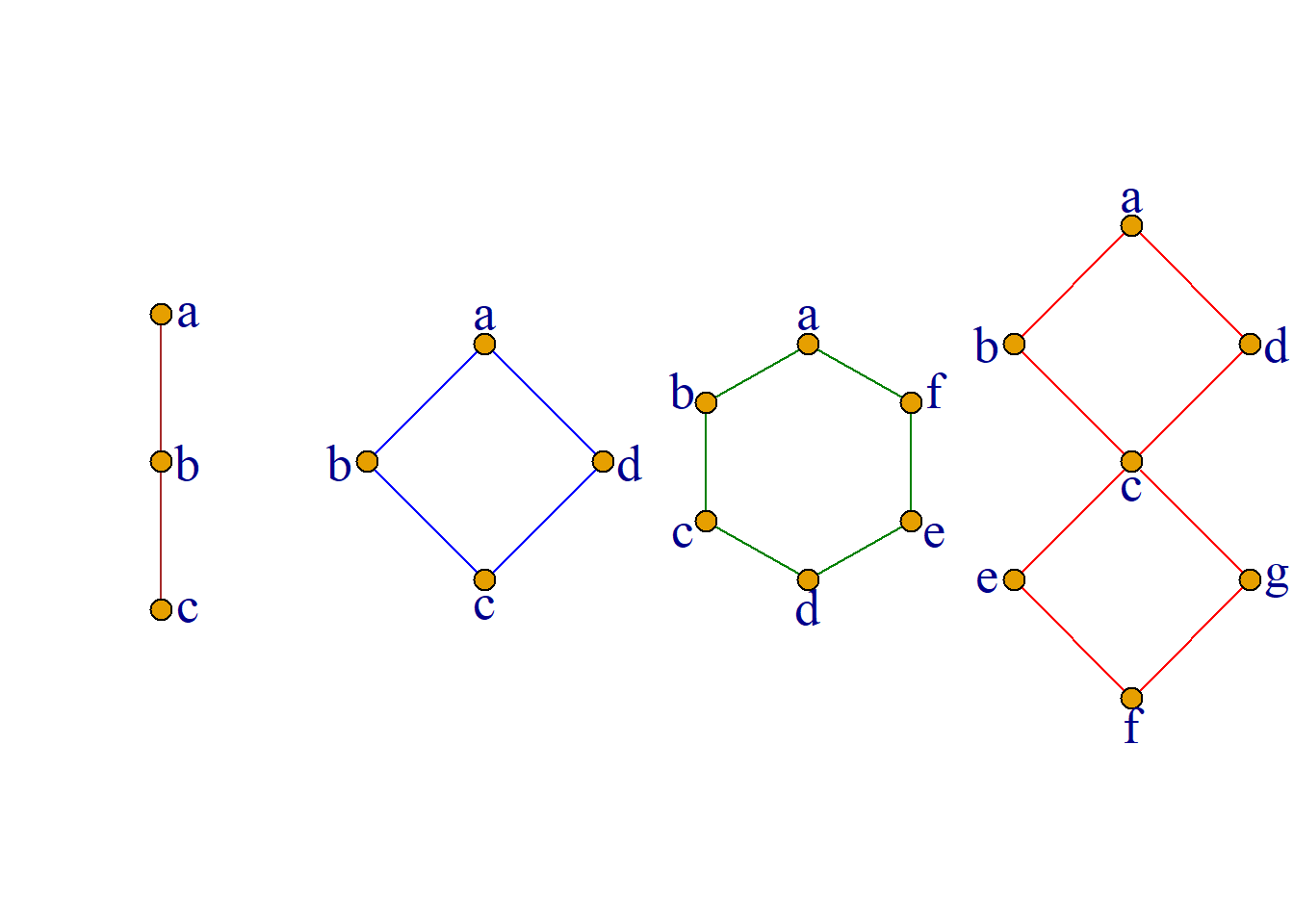
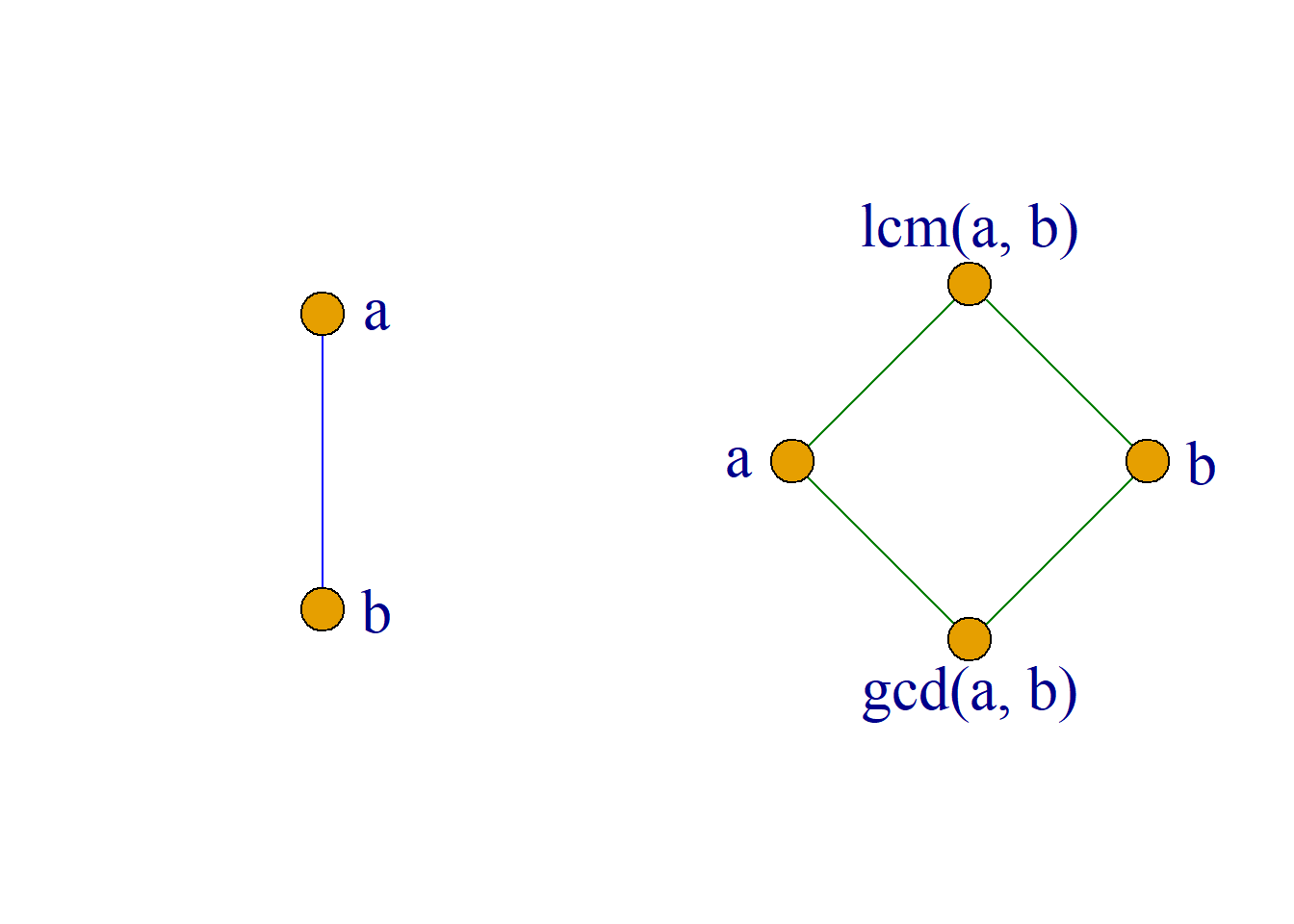
例: 设\(Z^+\)是正整数的集合, 在\(Z^+\)上定义整除关系|: 对于任意的\(a, b{\in}Z\) 对\({\forall}a, b{\in}Z^+\), \({\langle}a, b{\rangle}{\in}|\)当且仅当\(a\)整除\(b\), 则偏序集 \({\langle} Z, | {\rangle}\)是格.

证明:\[|=\{{\langle}a, b{\rangle}| a, b{\in}Z^+, a|b\}{\rangle}\] 对\({\forall}a, b{\in}Z^+\), 它们的最小上界和最大下界为两元素的最小公倍数和最大公约数, 即: \[a{\vee}b=lcm(a, b){\in}Z^+, \] \[a{\wedge}b=gcd(a, b){\in}Z^+,\] 故\({\langle}Z^+, |{\rangle}\)是格.

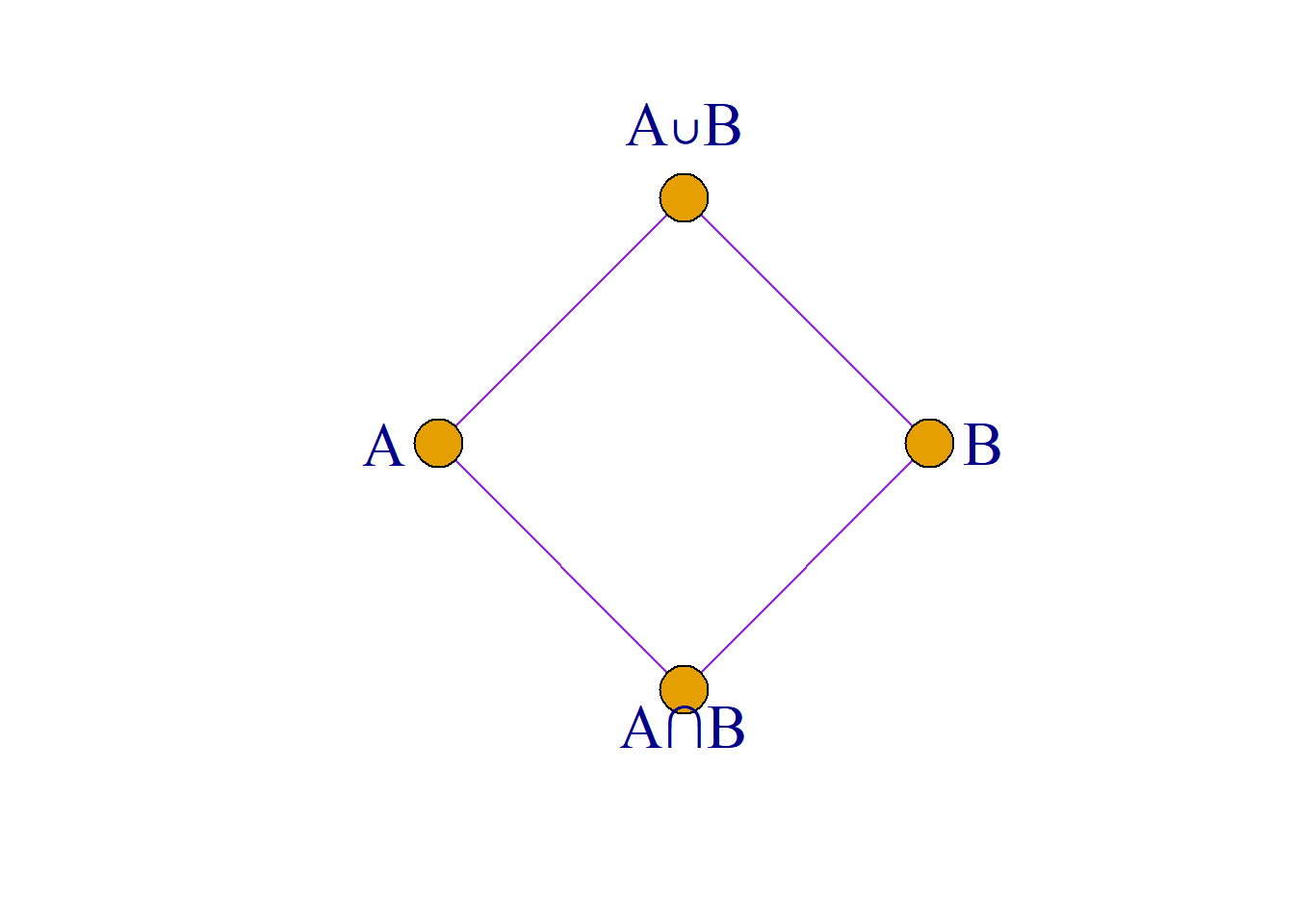
例: 对任意集合\(S, P(S)\)是\(S\)的幂集, 则偏序集\({\langle}P(S), \subseteq{\rangle}\)是格.

证明: \[{\subseteq} = \{{\langle}X, Y{\rangle}|X, Y{\in}P(S), X{\subseteq}Y\}\] 因为\({\subseteq}\)是\(P(S)\)上的偏序关系, 且\({\forall}A, B{\in}P(S)\), 它们的最小上界和最大下界分别为两集合的并集和交集.

即 \[A{\vee}B=A{\cup}B{\in}P(S)\] \[A{\wedge}B=A{\cap}B{\in}P(S)\] 所以它是格. \({\langle}P(S), {\subseteq}{\rangle}\)称为集合的幂集格.

例: 设\(S=\{a, b\}\),

\(P(S)=\{\phi, \{a\}, \{b\}, \{a, b\}\}\),

则\({\langle}P(S), {\subseteq}{\rangle}\)是格.

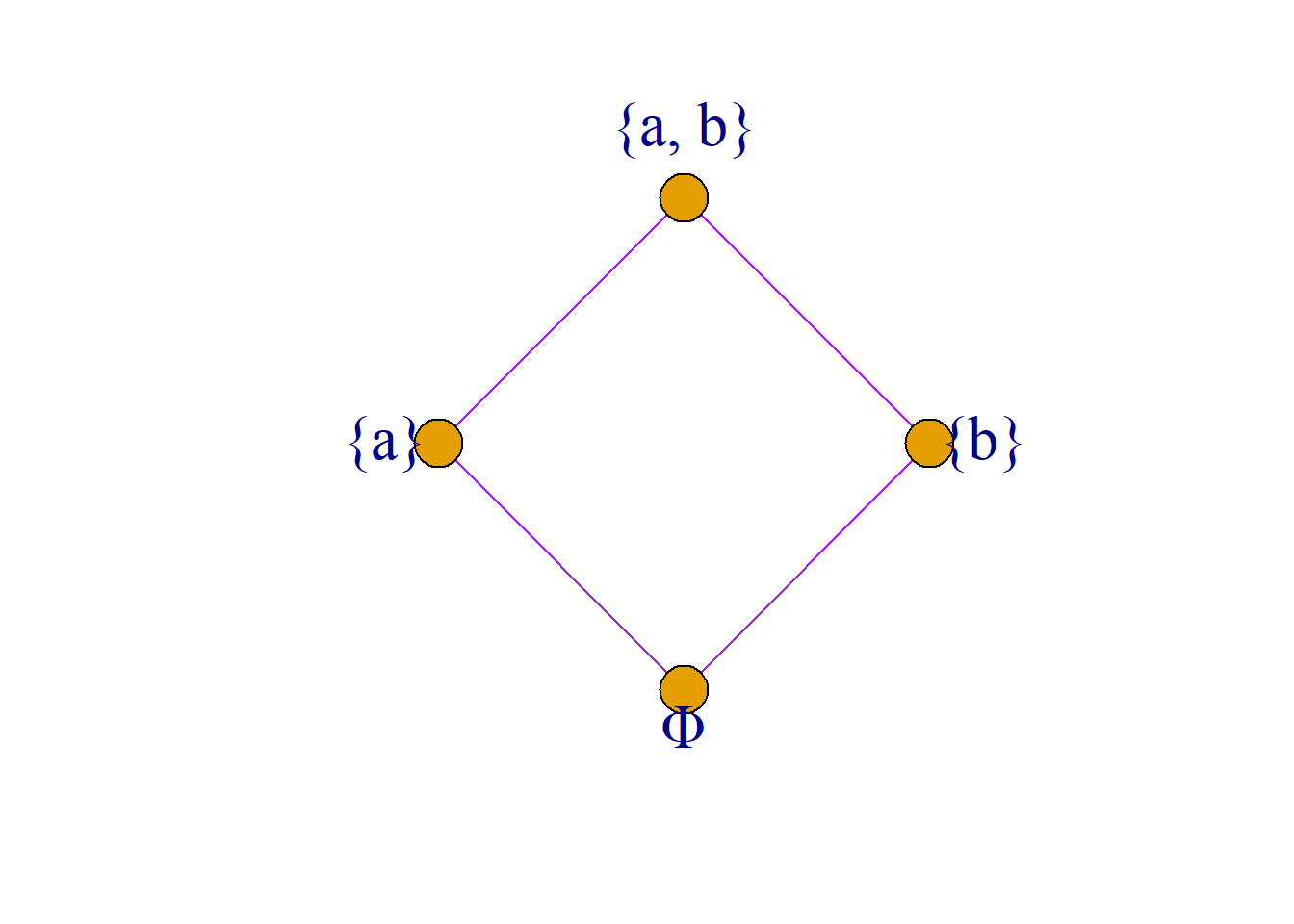
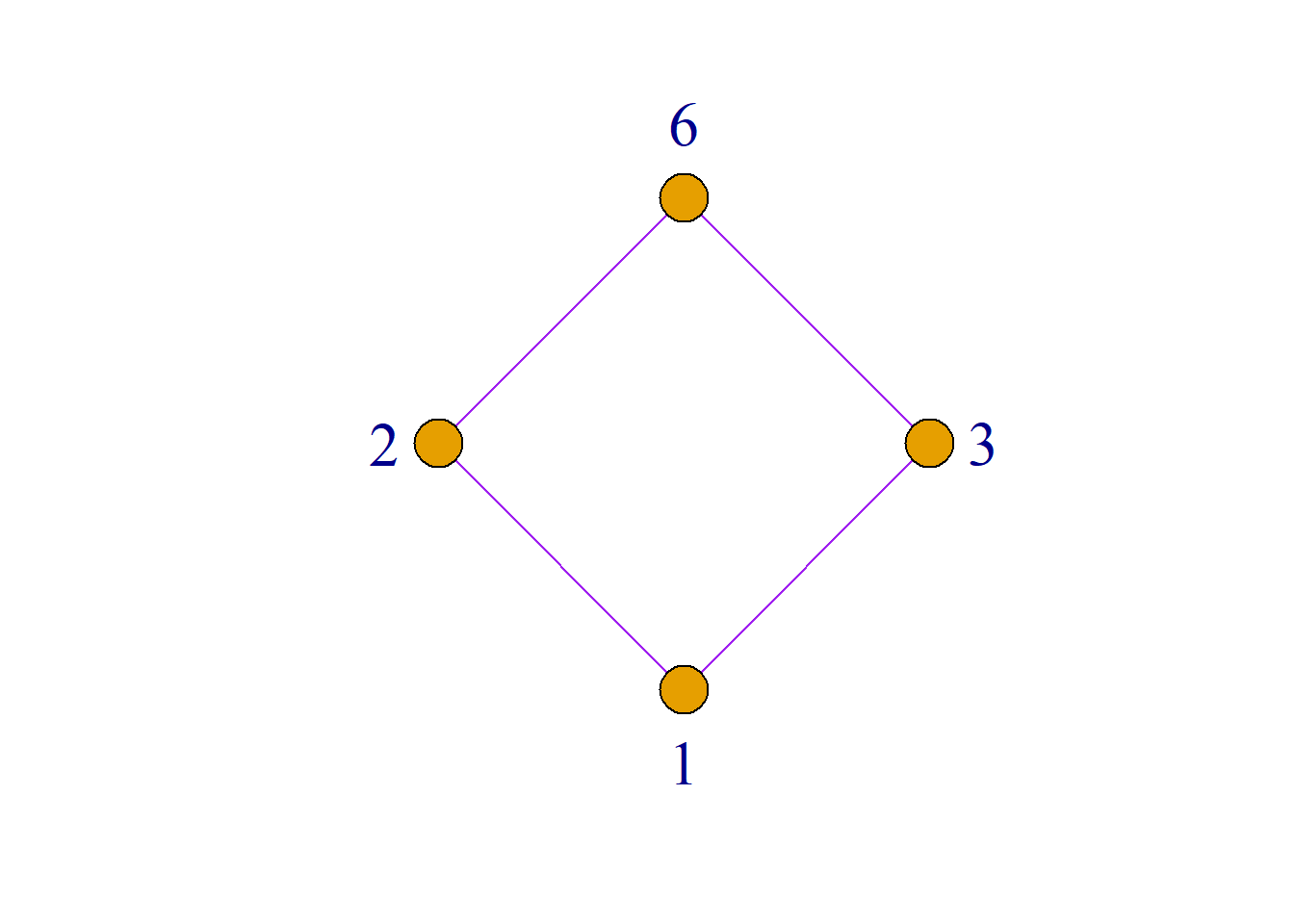
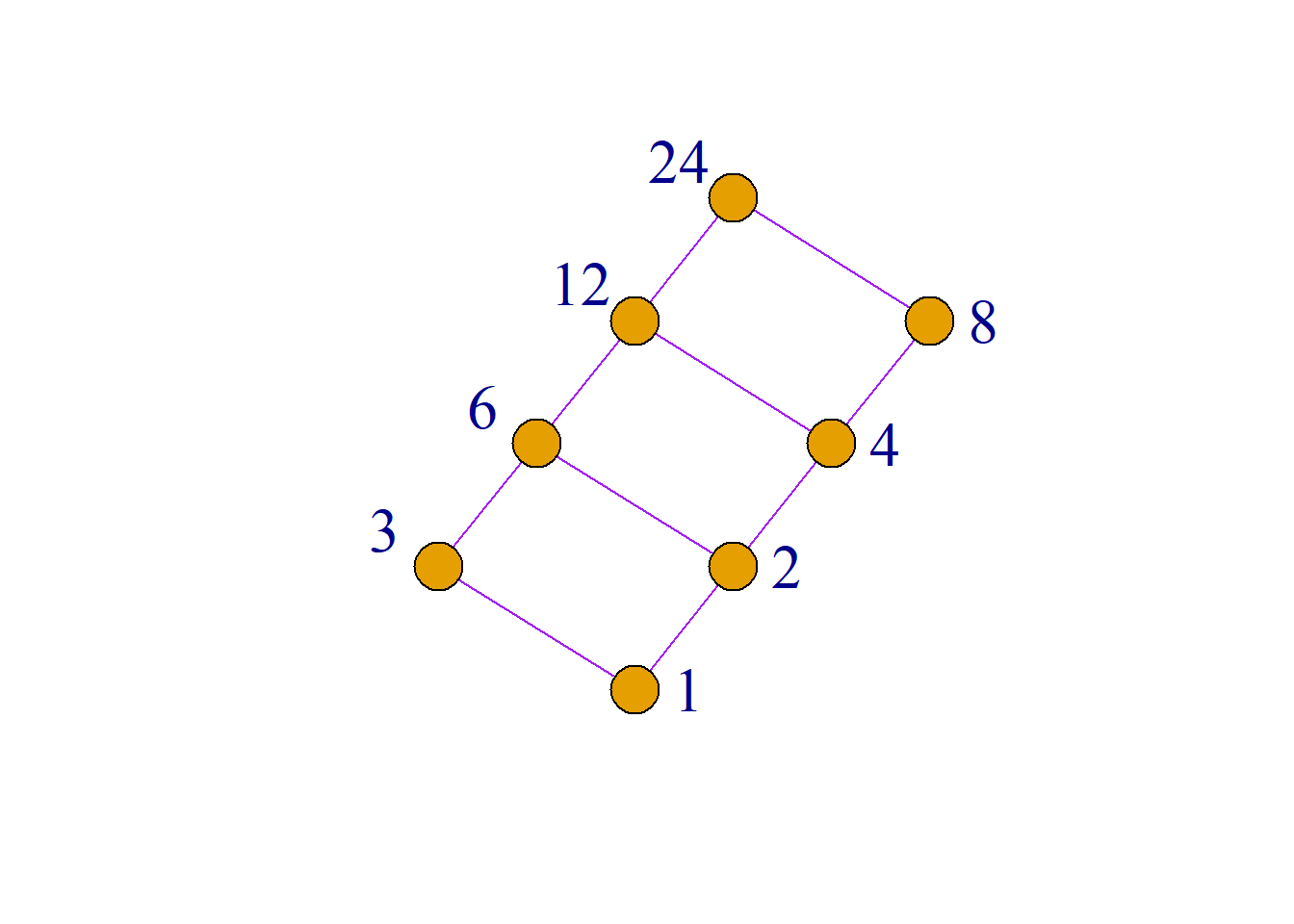
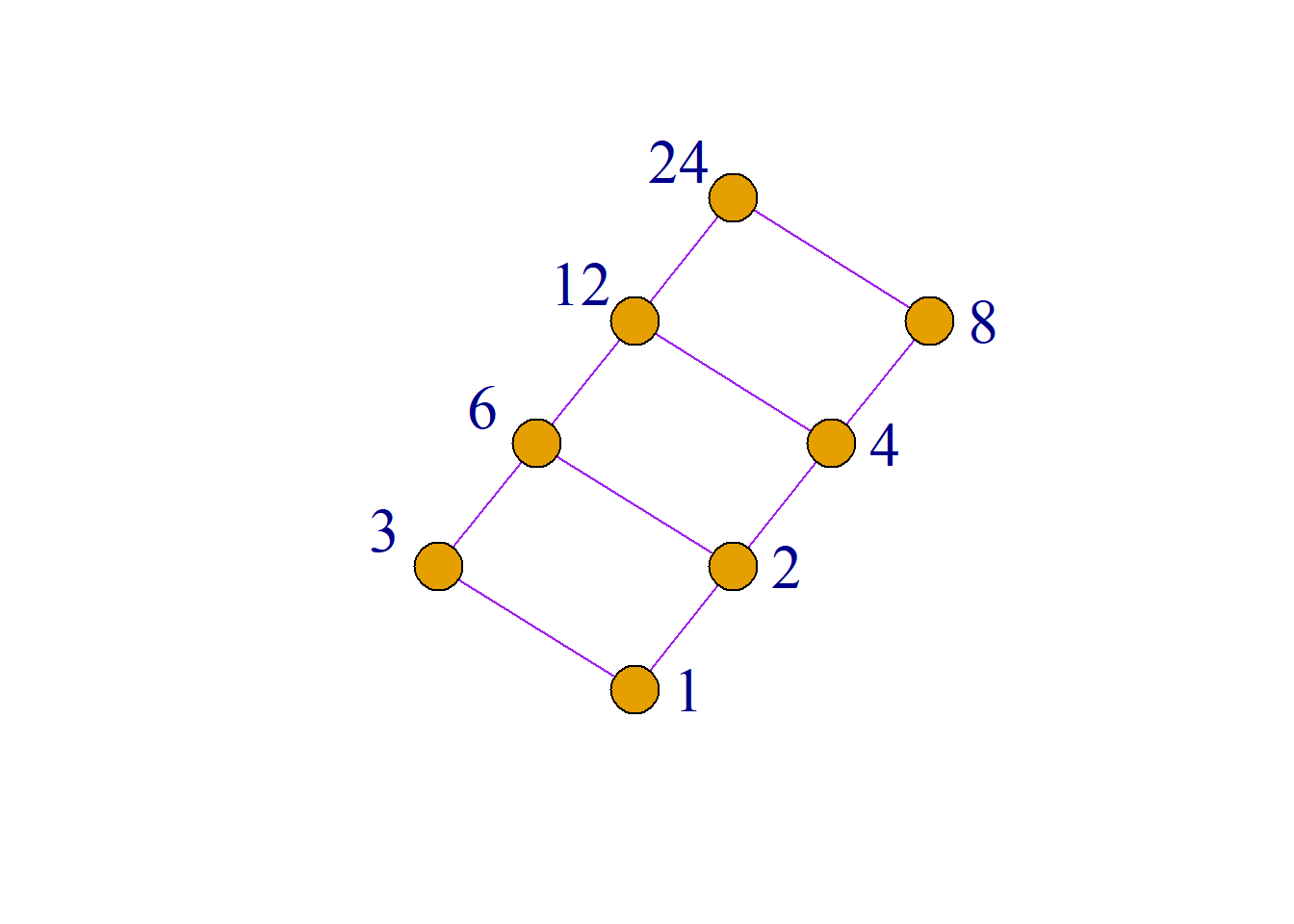
例: 设\(n\)是一个正整数, \(S_n\)是\(n\)的所有正因子的集合. 例如: \[S_6=\{1, 2, 3, 6\}\] \[S_8=\{1, 2, 4, 8\}\] \[S_{24}=\{1, 2, 3, 4, 6, 8, 12, 24\}\] 又设|是整除关系, 则偏序集\({\langle}S_n, |{\rangle}\)是格.

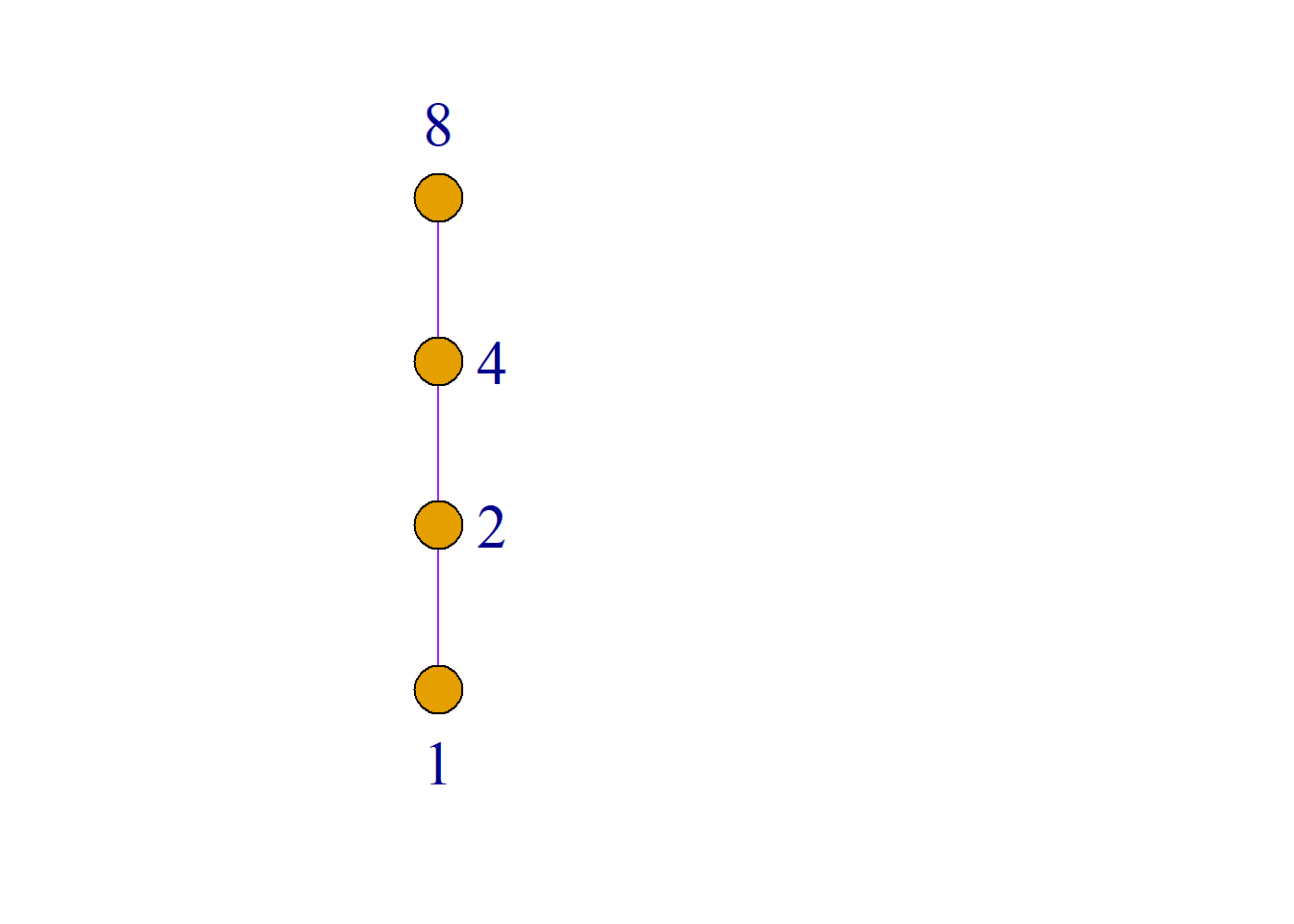
设\({\langle}L, {\leq}{\rangle}\)是格, \({\geq}\)是\({\leq}\)的逆关系, 则格\({\langle}L, {\geq}{\rangle}\)称为格\({\langle}L, {\leq}{\rangle}\)的对偶格(互为对偶格), 关系\({\leq}\)和关系\({\geq}\)称为互为对偶的关系.

定理: 若\({\langle}L, {\leq}{\rangle}\)是一个格, 则\({\langle}L, {\geq}{\rangle}\)也是一个格, 且格\({\langle}L, {\geq}{\rangle}\)中的保联运算和保交运算(用\({\bigoplus}\)和\({\bigotimes}\)表示)与格\({\langle}L, {\leq}{\rangle}\)中的保联运算和保交运算(用\({\vee}\)和\({\wedge}\)表示)满足如下的关系:

对\({\forall} a, b{\in}L\), 有\(a{\vee}b=a{\bigotimes}b, a{\wedge}b=a{\bigoplus}b\).

定义: 一个由格\({\langle}L, {\leq}{\rangle}\)中的元素以及符号\({\vee}, {\wedge}, =\)和\({\leq}\)所组成的命题\(P\)的对偶命题是指命题\(P^*\), 它是将\(P\)中的\({\leq}\)换为\({\geq}\), \({\vee}\)换为\({\wedge}\), \({\wedge}\)换为\({\vee}\)所得到的命题.

例如, 命题\((a{\vee}b){\wedge}c{\leq}c\)的对偶式为命题 \((a{\wedge}b){\vee}c{\geq}c\). 实际上, \((a{\vee}b){\wedge}c{\leq}c\)是格 \({\langle}L, {\leq}{\rangle}\)中的命题, 而\((a{\wedge}b){\vee}c{\geq}c\)是格\({\langle}L, {\geq}{\rangle}\)中的命题.

定理: (对偶原理)对于格\({\langle}L, {\leq}{\rangle}\)中的任一真命题\(P\), 其对偶命题\(P^*\)也是真命题.

例: 格\({\langle}P(S), {\subseteq}{\rangle}\)中的真命题\(A{\cap}B{\subseteq}A\)的对偶命题\(A{\cup}B{\supseteq}A\)(格\({\langle}P(S), {\supseteq}{\rangle}\)中)也是真命题.

定理: 设\({\langle}L, {\leq}{\rangle}\)为格, 则对L中任何元素\(a\), \(b\)和\(c\)有:

\(a{\leq}a{\vee}b, b{\leq}a{\vee}b\), \(a{\wedge}b{\leq}a, a{\wedge}b{\leq}b\)
若\(a{\leq}b, a{\leq}c\), 则:\(a{\leq}b{\wedge}c\). 若\(a{\leq}c, b{\leq}c\), 则:\(a{\vee}b{\leq}c\).
若\(a{\leq}b, c{\leq}d\), 则:\(a{\vee}c{\leq}b{\vee}d\), \(a{\wedge}c{\leq}b{\wedge}d\).
若\(b{\leq}c\), 则:\(a{\vee}b{\leq}a{\vee}c\), \(a{\wedge}b{\leq}a{\wedge}c\).

定理: 设\({\langle}L, {\leq}{\rangle}\)为格, 那么对\(L\)中任何元素\(a\), \(b\)和\(c\), 以下定律成立.

幂等律 \(a{\vee}a=a, a{\wedge}a=a\)
交换律 \(a{\vee}b=b{\vee}a, a{\wedge}b=b{\wedge}a\)
结合律 \((a{\vee}b){\vee}c=a{\vee}(b{\vee}c)\), \((a{\wedge}b){\wedge}c=a{\wedge}(b{\wedge}c)\)
吸收律 \(a{\vee}(a{\wedge}b)=a\), \(a{\wedge}(a{\vee}b)=a\)

定理: 设\({\langle}L, {\leq}{\rangle}\)为格, 则对L中任何元素\(a\)和\(b\), 有 \(a{\leq}b{\Leftrightarrow}a{\wedge}b=a{\Leftrightarrow}a{\vee}b=b.\)

定理: 设\({\langle}L, {\leq}{\rangle}\)为格, 则对\(L\)中任何元素\(a\), \(b\)和\(c\), 有:

\(a{\vee}(b{\wedge}c){\leq}(a{\vee}b){\wedge}(a{\vee}c)\).
\(a{\wedge}(b{\vee}c){\geq}(a{\wedge}b){\vee}(a{\wedge}c)\).

其中关系\({\geq}\)是关系\({\leq}\)的对偶关系.

定理: 设\({\langle}L, {\leq}{\rangle}\)为格, 那么对\(L\)中任何元素\(a\), \(b\)和\(c\), 有: \(a{\leq}c{\Leftrightarrow}a{\vee}(b{\wedge}c){\leq}(a{\vee}b){\wedge}c.\)

\[ \begin{array}{ll} {\langle}L, {\leq}{\rangle}& {\langle}L, {\geq}{\rangle}\\ a{\leq}a & a{\geq}a \\ a{\leq}b{且}b{\leq}a{\Rightarrow}a=b&a{\geq}b{且}b{\geq}a{\Rightarrow}a=b\\ a{\leq}b{且}b{\leq}c{\Rightarrow}a{\leq}c&a{\geq}b{且}b{\geq}c{\Rightarrow}a{\geq}c\\ a{\wedge}b{\leq}a;a{\wedge}b{\leq}b&a{\bigoplus}b{\geq}a;a{\bigoplus}b{\geq}b\\ c{\leq}a{且}c{\leq}b{\Rightarrow}c{\leq}a{\wedge}b&c{\geq}a{且}c{\geq}b{\Rightarrow}c{\geq}a{\bigoplus}b\\ a{\wedge}b=b{\wedge}a & a{\bigoplus}b=b{\bigoplus}a \\ (a{\wedge}b){\wedge}c=a{\wedge}(b{\wedge}c) & (a{\bigoplus}b){\bigoplus}c=a{\bigoplus}(b{\bigoplus}c)\\ a{\wedge}(a{\vee}b)=a & a{\bigoplus}(a{\bigotimes}b)=a\\ a{\wedge}a=a & a{\bigoplus}a=a\\ \end{array} \]

\[ \begin{array}{ll} {\langle}L, {\leq}{\rangle}& {\langle}L, {\geq}{\rangle}\\ a{\leq}b{\Rightarrow}a{\wedge}b=a & a{\geq}b{\Rightarrow}a{\bigoplus}b=a\\ a{\leq}b{\Rightarrow}a{\vee}b=b & a{\geq}b{\Rightarrow}a{\bigotimes}b=b\\ a{\leq}b{且}c{\leq}d& a{\geq}b{且}c{\geq}d\\ {\Rightarrow}a{\wedge}c{\leq}b{\wedge}d & {\Rightarrow}a{\bigoplus}c{\geq}b{\bigoplus}d\\ a{\leq}b{\Rightarrow}a{\wedge}c{\leq}b{\wedge}c & a{\geq}b{\Rightarrow}a{\bigoplus}c{\geq}b{\bigoplus}c \\ a{\vee}(b{\wedge}c){\leq}(a{\vee}b){\wedge}(a{\vee}c) & a{\bigotimes}(b{\bigoplus}c){\geq}(a{\bigotimes}b){\bigoplus}(a{\bigotimes}c)\\ a{\leq}c{\Leftrightarrow} & a{\geq}c{\Leftrightarrow}\\ a{\vee}(b{\wedge}c){\leq}(a{\vee}b){\wedge}c & a{\bigotimes}(b{\bigoplus}c){\leq}(a{\bigotimes}b){\bigoplus}c \end{array} \]

代数系统定义的格

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)(或\({\langle}L, {\wedge}, {\vee}{\rangle}\))是代数系统, \({\vee}\)和\({\wedge}\)是\(L\)上的两个二元运算, 如果这两个运算对\(L\)中的元素满足:

交换律 \(a{\vee}b=b{\vee}a\), \(a{\wedge}b=b{\wedge}a\)
结合律 \((a{\vee}b){\vee}c=a{\vee}(b{\vee}c)\), \((a{\wedge}b){\wedge}c=a{\wedge}(b{\wedge}c)\)
吸收律 \(a{\vee}(a{\wedge}b)=a\), \(a{\wedge}(a{\vee}b)=a\)

则称代数系统\({\langle}L, {\vee}, {\wedge}{\rangle}\)是格.也称这样定义的格为代数格.

定理: 由代数系统定义的格和由偏序集定义的格是等价的. 亦即, 一个代数格必是一个偏序格;一个偏序格必是一个代数格.

例: 对任意集合\(S, P(S)\)是\(S\)的幂集, 集合的并集\({\cup}\)和交集\({\cap}\)是\(P(S)\)上的两个二元运算, 满足交换律, 结合律和吸收律, 因此\({\langle}P(S), {\cup}, {\cap}{\rangle}\)是格.

它与前面曾提到的格\({\langle}P(S), {\subseteq}{\rangle}\)是一致的, 且对于任意的\(A, B{\in}P(S)\), 有 \[A{\subseteq}B{\Leftrightarrow}A{\cap}B=A{\Leftrightarrow}A{\cup}B=B.\]

例: 对代数系统\({\langle}N, {\vee}, {\wedge}{\rangle}\), 两个二元运算\({\vee}\), \({\wedge}\)分别定义为:对\({\forall}a, b{\in}N\), \(a{\vee}b=max\{a, b\}, a {\wedge} b=min\{a, b\}\). 求证: \({\langle}N, {\vee}, {\wedge}{\rangle}\)是一个格.

证明:

交换律. \({\forall}a, b{\in}N\), \(a{\vee}b=max\{a, b\}=max\{b, a\}=b{\vee}a\).
结合律. \({\forall}a, b, c{\in}N\), \(a{\vee}(b{\vee}c)=max(a, max\{b, c\})=max(a, b, c) = max(max(a, b), c)=(a{\vee}b){\vee}c\). \(\,\,a{\wedge}(b{\wedge}c)=min(a, min\{b, c\})=min(a, b, c) =min(min(a, b), c)=(a{\wedge}b){\wedge}c\).
吸收律. \({\forall}a, b, c{\in}N\), \(a{\vee}(a{\wedge}b)= a{\vee}min(a, b)=max(a, min(a, b))=a\), \(a{\wedge}(a{\vee}b)= a{\wedge}max(a, b)=min(a, max(a, b))=a\).

所以\({\langle}N, {\vee}, {\wedge}{\rangle}\)是一个格. 同样, \({\langle}Z, {\vee}, {\wedge}{\rangle}\)也是一个格. \({\langle}N, {\vee}, {\wedge}{\rangle}\)和\({\langle}Z, {\vee}, {\wedge}{\rangle}\)对应的偏序格是\({\langle}N, {\leq}{\rangle}\)和\({\langle}Z, {\leq}{\rangle}\), 即自然数集合上的小于等于关系, 整数集合上的小于等于关系构成的格.

子格与格的同态

子格

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是格, \(S\)是\(L\)的非空子集, 如果\({\langle}S, {\vee}, {\wedge}{\rangle}\)仍构成一个格, 则称\({\langle}S, {\vee}, {\wedge}{\rangle}\)是\({\langle}L, {\vee}, {\wedge}{\rangle}\)的子格.

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是格, \(S\)是\(L\)的非空子集, 若对\(S\)中的任意元素\(a\)和\(b\), 有:

\(a{\vee}b{\in}S\)
\(a{\wedge}b{\in}S\)

则称\({\langle}S, {\vee}, {\wedge}{\rangle}\)是\({\langle}L, {\vee}, {\wedge}{\rangle}\)的子格.

子格必是格. 因为当运算限制在\(S\)上时, 交换律、结合律和吸收律也是成立的.

例: 设\({\langle}Z, {\vee}, {\wedge}{\rangle}\)是格, 两个二元运算\({\vee}\)和\({\wedge}\)为:

对任意\(a, b{\in}Z\), 有: \(a{\vee}b=max\{a, b\}, \,\,a{\wedge}b=min\{a, b\}\).

又设\(Z^+\)是所有正整数的集合, 显然\(Z^+{\subseteq}Z\)且非空, 且对于任意\(a, b{\in}Z^+\), 有: \[a{\vee}b=max\{a, b\}{\in}Z^+, \,\,a{\wedge}b=min\{a, b\}{\in}Z^+.\] 因此, \({\langle} Z^+, {\vee}, {\wedge}{\rangle}\)是\({\langle}Z, {\vee}, {\wedge}{\rangle}\)的子格.

对应的偏序格为: \({\langle}Z^+, {\leq}{\rangle}\)和\({\langle}Z, {\leq}{\rangle}\).

当格是以偏序集\({\langle}L, {\leq}{\rangle}\)的形式定义时, 子格的另一种定义:

定义: 设\({\langle}L, {\leq}{\rangle}\)是格, \(S\)是\(L\)的非空子集, 若对于任意\(a, b{\in}S\), \(\{a, b\}\)在\(L\)中求得的最小上界\(a{\vee}b\)和最大下界\(a{\wedge}b\)仍在\(S\)中, 则称\({\langle}S, {\leq}{\rangle}\)是\({\langle}L, {\leq}{\rangle}\)的子格.

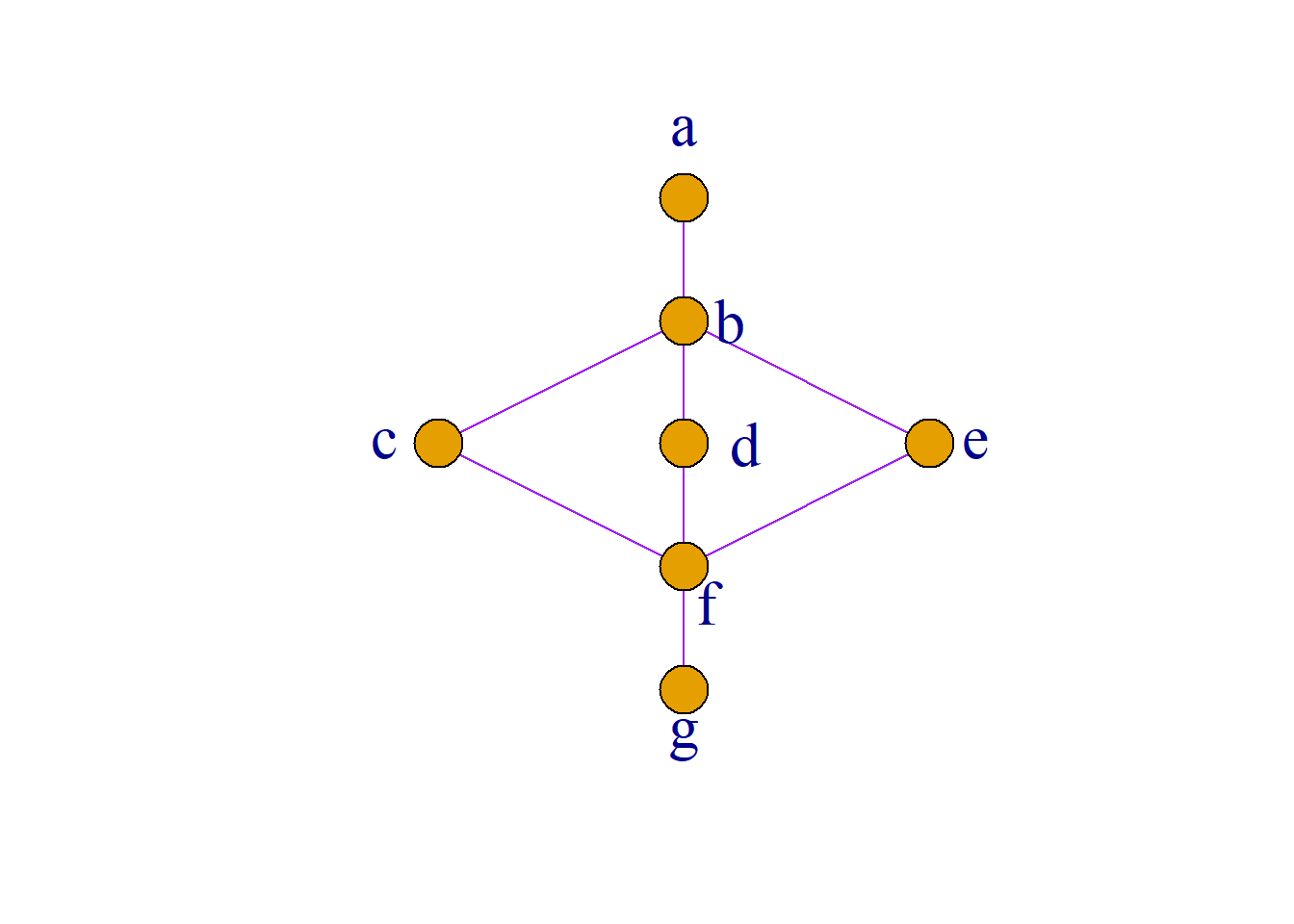
例: 设\({\langle}L, {\leq}{\rangle}\)是格, 其中: \[L=\{a, b, c, d, e, f, g, h, \},\] 哈斯图如图所示:

取\[S_1=\{a, b, d, f\}\] \[S_2=\{c, e, g, h\}\] \[S_3=\{a, b, c, d, e, g, h\}\] 判断\(S_1\), \(S_2\)和\(S_3\)哪个可以构成\(L\)的子格.

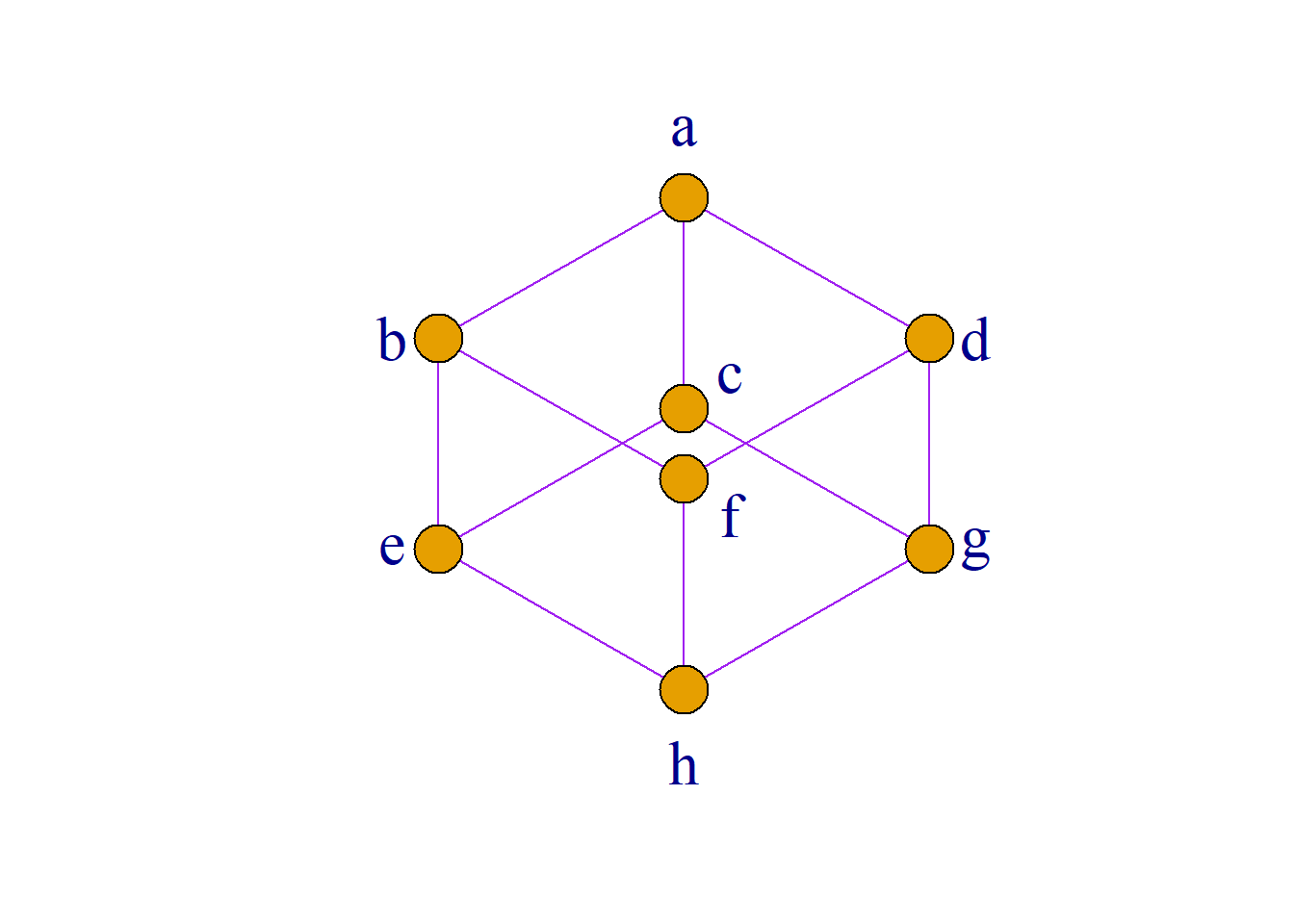
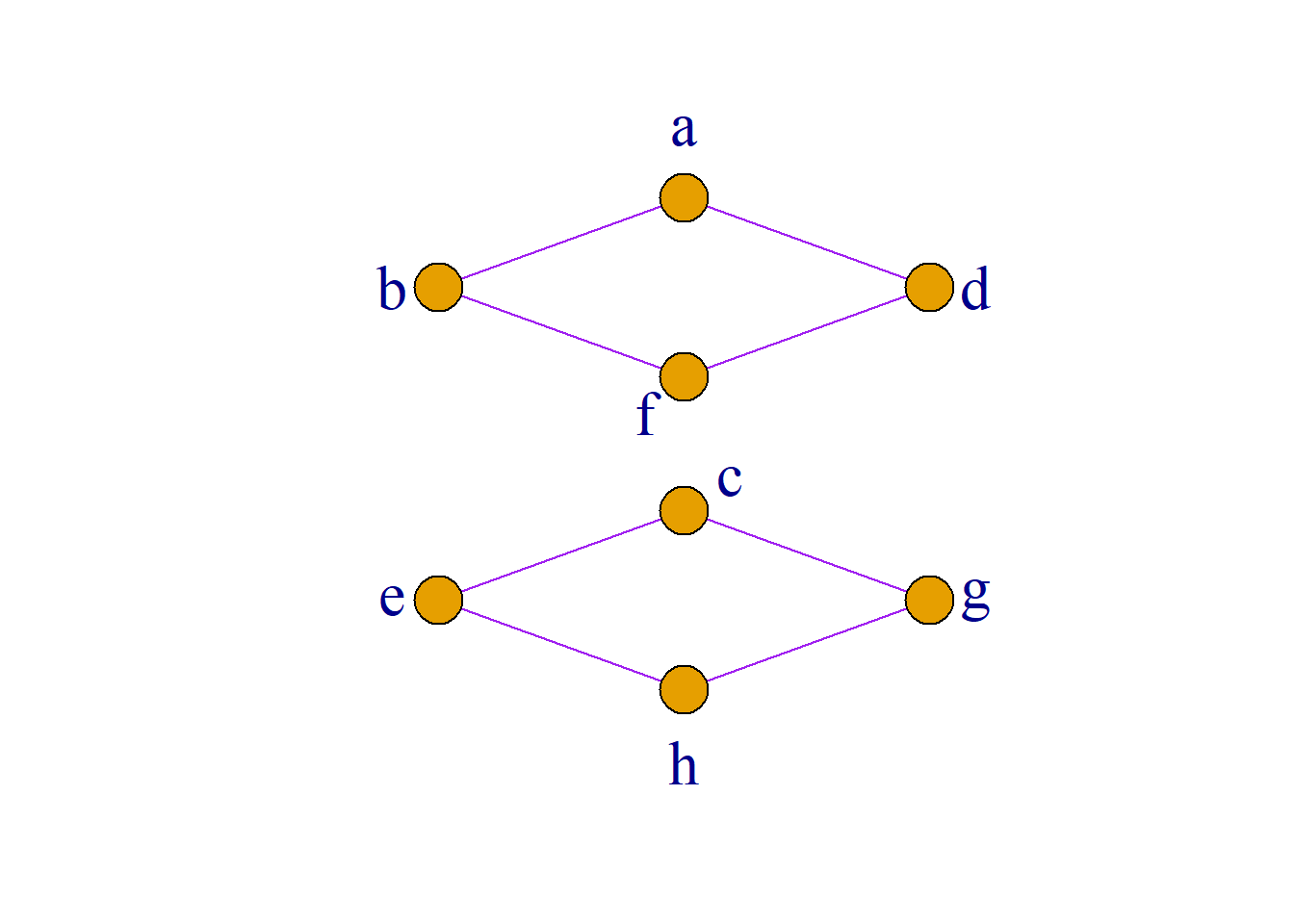
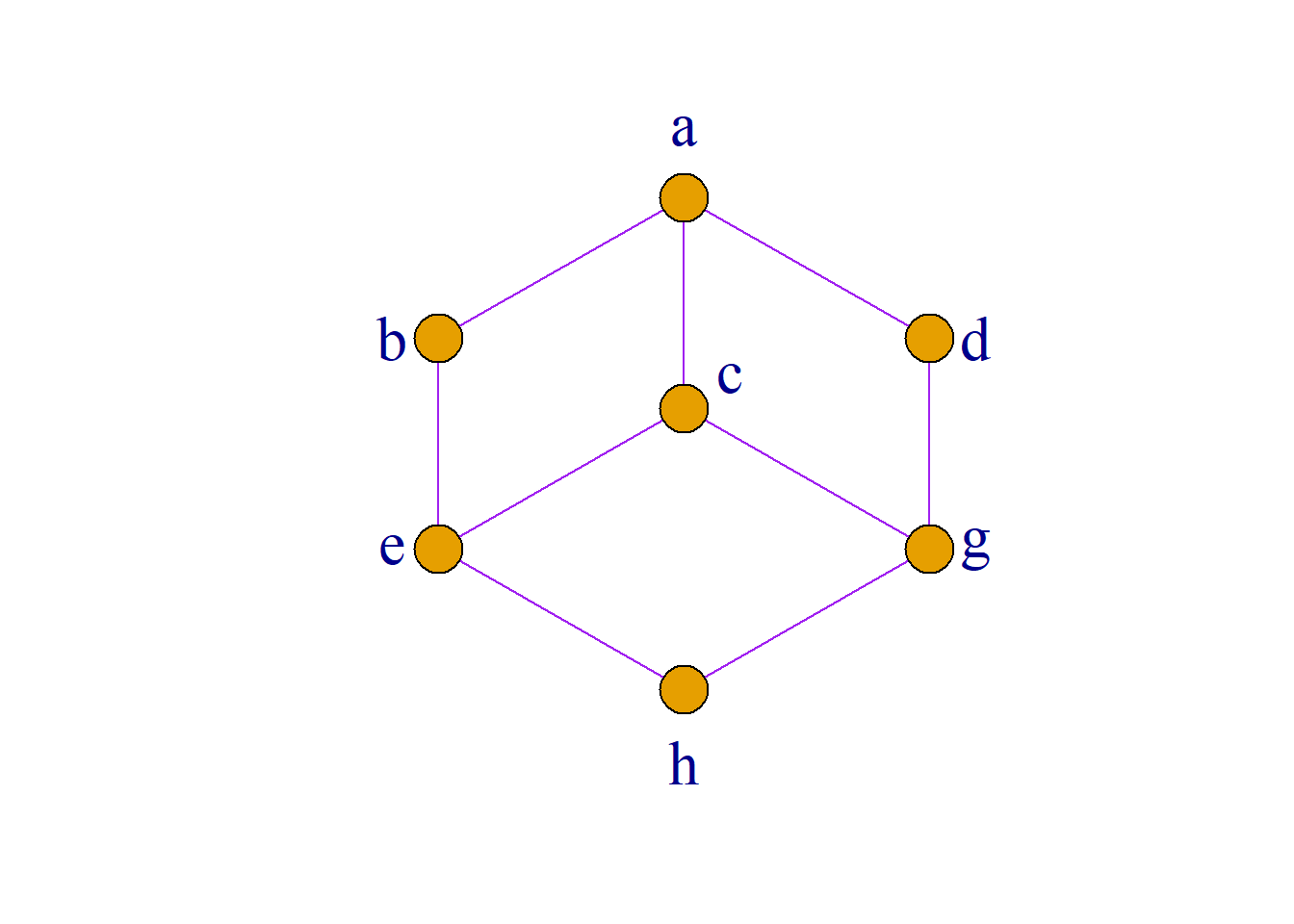
S₃:{a, b, c, d, e, g, h}, S₃是格, 但不是L的子格, 因为b和d的最大下界f不在S₃内.

例: 设\({\langle}L, {\leq}{\rangle}\)是一个格, \(a{\in}L, S{\subseteq}L\)定义为: \[S=\{x|x{\in}L, a{\leq}x\}\] 则\({\langle}S, {\leq}{\rangle}\)是\({\langle}L, {\leq}{\rangle}\)的子格.

证明:对\({\forall}x_1, x_2{\in}S{\subseteq}L\), 有: \[x_1{\vee}x_2{\in}L, x_1{\wedge}x_2{\in}L,\,\,\,a{\leq}x_1, a{\leq}x_2\] 可得: \(a{\leq}x_1{\vee}x_2\), \(a{\leq}x_1{\wedge}x_2\),

因此: \(x_1{\vee}x_2{\in}S\), \(x_1{\wedge}x_2{\in}S\),

故\({\langle}S, {\leq}{\rangle}\)是\({\langle}L, {\leq}{\rangle}\)的子格.

格的同态

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)和\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)是两个格, 若存在映射\(f\):\(L{\rightarrow}S\), 使对\({\forall}a, b{\in}L\), 有:

\[f(a{\vee}b)=f(a){\bigoplus}f(b)\] \[f(a{\wedge}b)= f(a){\bigotimes}f(b)\]

则称\(f\)是\({\langle}L, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)的格同态映射, 简称同态映射.

若\(f\)是单射, 满射或双射时, 则称\(f\)分别是单同态映射, 满同态映射和同构映射.

特别地, \({\langle}L, {\vee}, {\wedge}{\rangle}\)到\({\langle}L, {\vee}, {\wedge}{\rangle}\)的格同态映射称为自同态映射; \({\langle}L, {\vee}, {\wedge}{\rangle}\)到\({\langle}L, {\vee}, {\wedge}{\rangle}\)的格同构映射称为自同构映射.

若\({\langle}L, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)存在同构映射, 则称 \({\langle}L, {\vee}, {\wedge}{\rangle}\)和\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)是同构的. 同构的两个格其哈斯图是相同的.

例: 设\({\langle}Z^+, {\vee}, {\wedge}{\rangle}\)是格, 其中\({\vee}, {\wedge}\)定义为对任意\(m, n{\in}Z^+\), 有: \[m{\vee}n=max\{m, n\}, m{\wedge}n=min\{m, n\}\] 另设格\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\), 其中: \(S=\{3^k|k{\in}Z^+\}\). 在\(S\)上定义二元运算\({\bigoplus}\)和\({\bigotimes}\)为:对任意\(3^m, 3^n{\in}S\), 有: \[3^m{\bigoplus}3^n=3^{max\{m, n\}},\,\,\,3^m{\bigotimes}3^n=3^{min\{m, n\}}.\]

定义\(Z^+\)到\(S\)的双射函数\(f:m{\rightarrow}3^m\). 求证:\(f\)是\({\langle}Z^+, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)的同构映射.

证明:对\({\forall}m, n{\in}Z^+\).

\[f (m{\vee}n) = f (max\{m, n\})=3^{max\{m, n\}}=3^m{\bigoplus}3^n = f (m){\bigoplus}f (n)\] \[f (m{\wedge}n) = f (min\{m, n\})=3^{min\{m, n\}}=3^m{\bigotimes}3^n = f (m){\bigotimes}f (n)\] 因此, \(f\)是\({\langle} Z^+, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)的格同态映射.

又因为\(f\)是双射的, 故\(f\)也是\({\langle}Z^+, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)的同构映射.

定义: 设\({\langle}L, {\leq}_L{\rangle}\)和\({\langle}S, {\leq}_S{\rangle}\)是两个格, 若存在映射\(f:L{\rightarrow}S\), 使对\(L\)中任意元素\(a\), \(b\). 当\(a{\leq}_Lb\)时, 有 \(f(a){\leq}_Sf(b)\), 则称\(f\)是\({\langle}L, {\leq}_L{\rangle}\)到\({\langle}S, {\leq}_S{\rangle}\)的格保序映射(序同态映射), 简称保序映射.

定理: 设\({\langle}L, {\leq}_L{\rangle}\)和\({\langle}S, {\leq}_S{\rangle}\)是两个格.

映射\(f:L{\rightarrow}S\), 如果\(f\)是\({\langle}L, {\vee}, {\wedge}{\rangle}\)到\({\langle}S, {\bigoplus}, {\bigotimes}{\rangle}\)同态映射, 则\(f\)是保序映射.

即对任意\(a, b{\in}L\), 若\(a{\leq}_Lb\), 有: \(f(a){\leq}_Sf(b)\).

其中:\({\leq}_L\)是集合\(L\)上对应于运算\({\vee}\)和\({\wedge}\)的偏序关系, \({\leq}_S\)为集合\(S\)上对应于运算\({\bigoplus}\)和\({\bigotimes}\)的偏序关系.

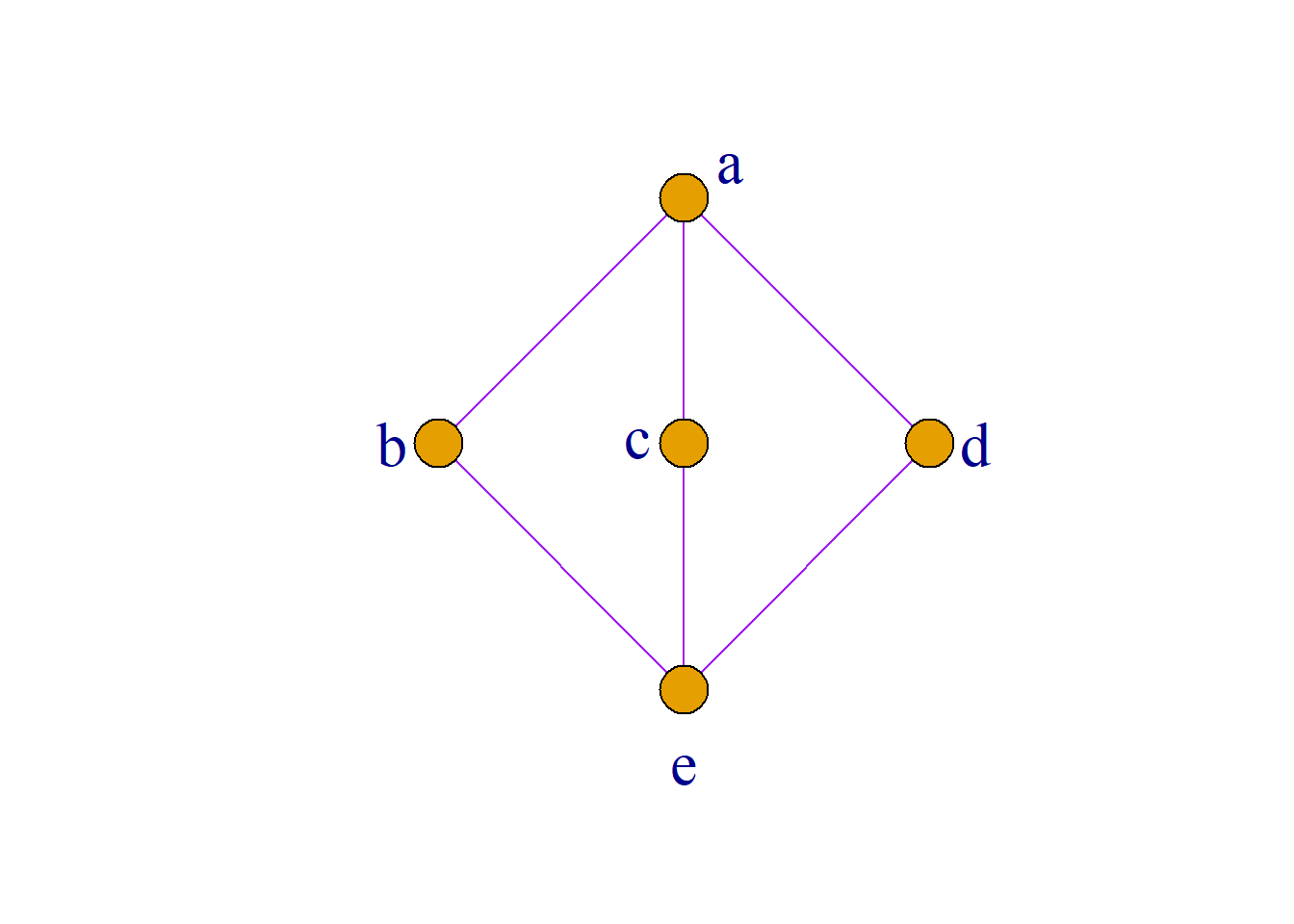
例: \({\langle}S, {\leq}{\rangle}\)是一个格, 其中 \(S=\{a, b, c, d, e\}\), 如图, \({\langle}P(S), {\subseteq}{\rangle}\)是幂集格. 定义映射: \(f:S{\rightarrow}P(S)\), 使\({\forall}x{\in}S\), 有: \[f(x)=\{y|y{\in}S, y{\leq}x\}\] 问\(f\)是否是保序映射？是否是同态映射？

解: \(f(a)=\{y|y{\in}S, y{\leq}a\}=\{a, b, c, d, e\}\) \[f(b)=\{y|y{\in}S, y{\leq}b\}=\{b, e\}\] \[f(c)=\{y|y{\in}S, y{\leq}c\}=\{c, e\}\] \[f(d)=\{y|y{\in}S, y{\leq}d\}=\{d, e\}\] \[f(e)=\{y|y{\in}S, y{\leq}e\}=\{e\}\] 当\(x{\leq}y\)时\(f(x){\subseteq}f(y)\), 故\(f\)是保序映射.

但是, \(b{\vee}d=a\), \(f(b{\vee}d){\neq}f(b){\cup}f(d)\). 故\(f\)不是同态映射.

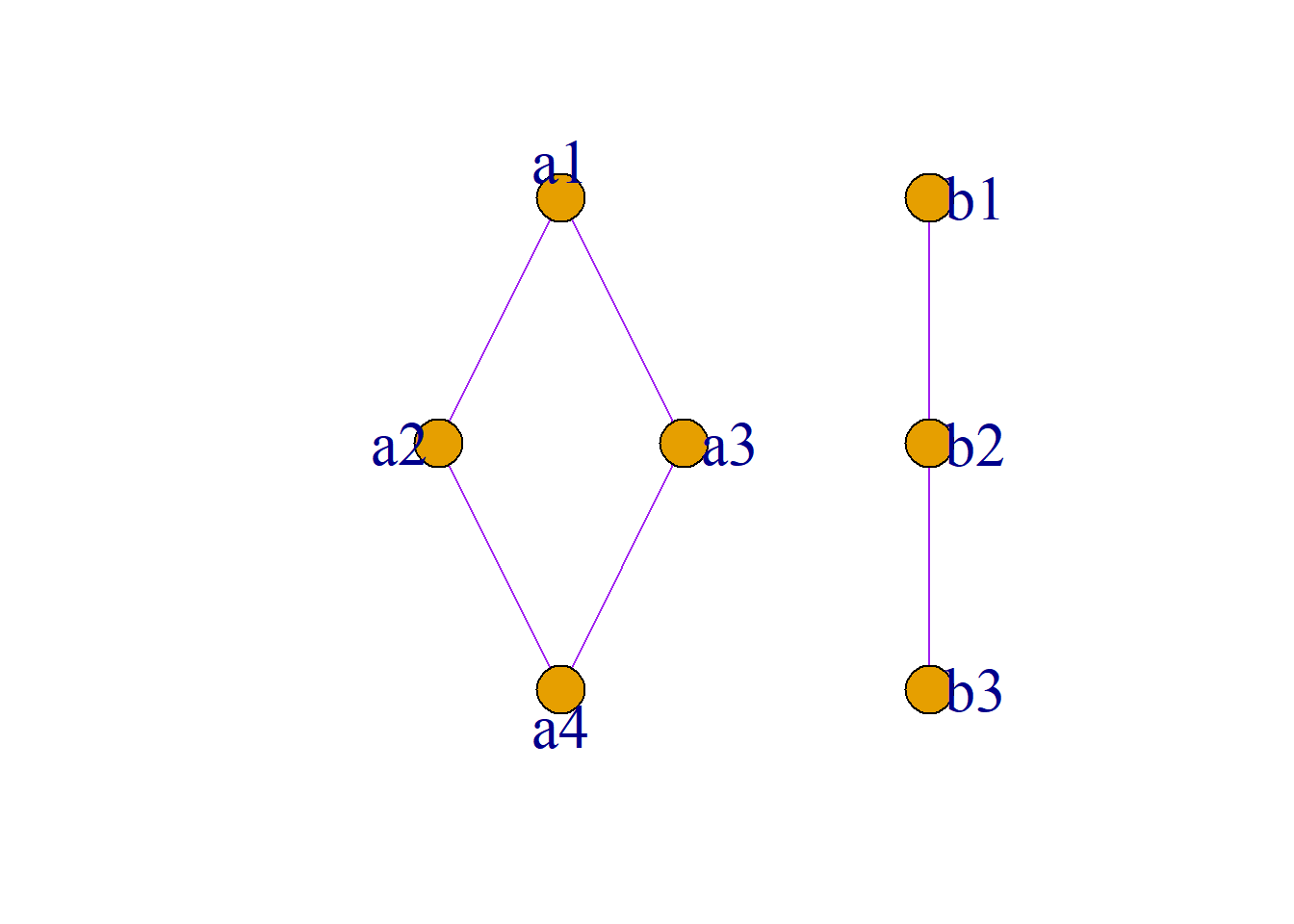
例: 如图所示的两哈斯图所表示的格\({\langle}L, {\leq}_L{\rangle}\)和\({\langle}S, {\leq}_S{\rangle}\), 定义映射:

\(f(a_1)=b_1\), \(f(a_2)= b_2\)

\(f(a_3)= b_2\), \(f(a_4)= b_3\)

显然\(f\)是\({\langle}L, {\leq}_L{\rangle}\)到\({\langle}S, {\leq}_S{\rangle}\)的保序映射;

但不是同态映射. 因为:

\(f(a_2{\vee}_La_3)=f(a_1)=b_1\),

\(f(a_2){\vee}_Sf(a_3)=b_2{\vee}_Sb_2 =b_2\),

\(f(a_2{\vee}_{L}a_3){\neq}f(a_2){\vee}_Sf(a_3)\).

分配格和有补格

分配格

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是一个格, 若\({\vee}\)对\({\wedge}\), \({\wedge}\)对\({\vee}\)均满足分配律, 即对任意\(a, b, c{\in}L\), 有: \[a{\vee}(b{\wedge}c) = (a{\vee}b){\wedge}(a{\vee}c)\] \[a{\wedge}(b{\vee}c) = (a{\wedge}b){\vee}(a{\wedge}c)\] 则称\({\langle}L, {\vee}, {\wedge}{\rangle}\)是分配格.

试证明: \({\langle}P(S), {\cup}, {\cap}{\rangle}\)是分配格. 其中\(S\)为任意集合, \(P(S)\)是\(S\)的幂集, \({\cup}\)是集合的并集, \({\cap}\)是集合的交集.

证明: 由于\({\langle}P(S), {\cup}, {\cap}{\rangle}\)是一个格, 且对于任意的\(A, B, C{\in}P(S)\), 有 \[A{\cup}(B{\cap}C)=(A{\cup}B){\cap}(A{\cup}C),\,\,\,A{\cap}(B{\cup}C)=(A{\cap}B){\cup}(A{\cap}C)\] 成立, 所以\({\langle}P(S), {\cup}, {\cap}{\rangle}\)是一个分配格.

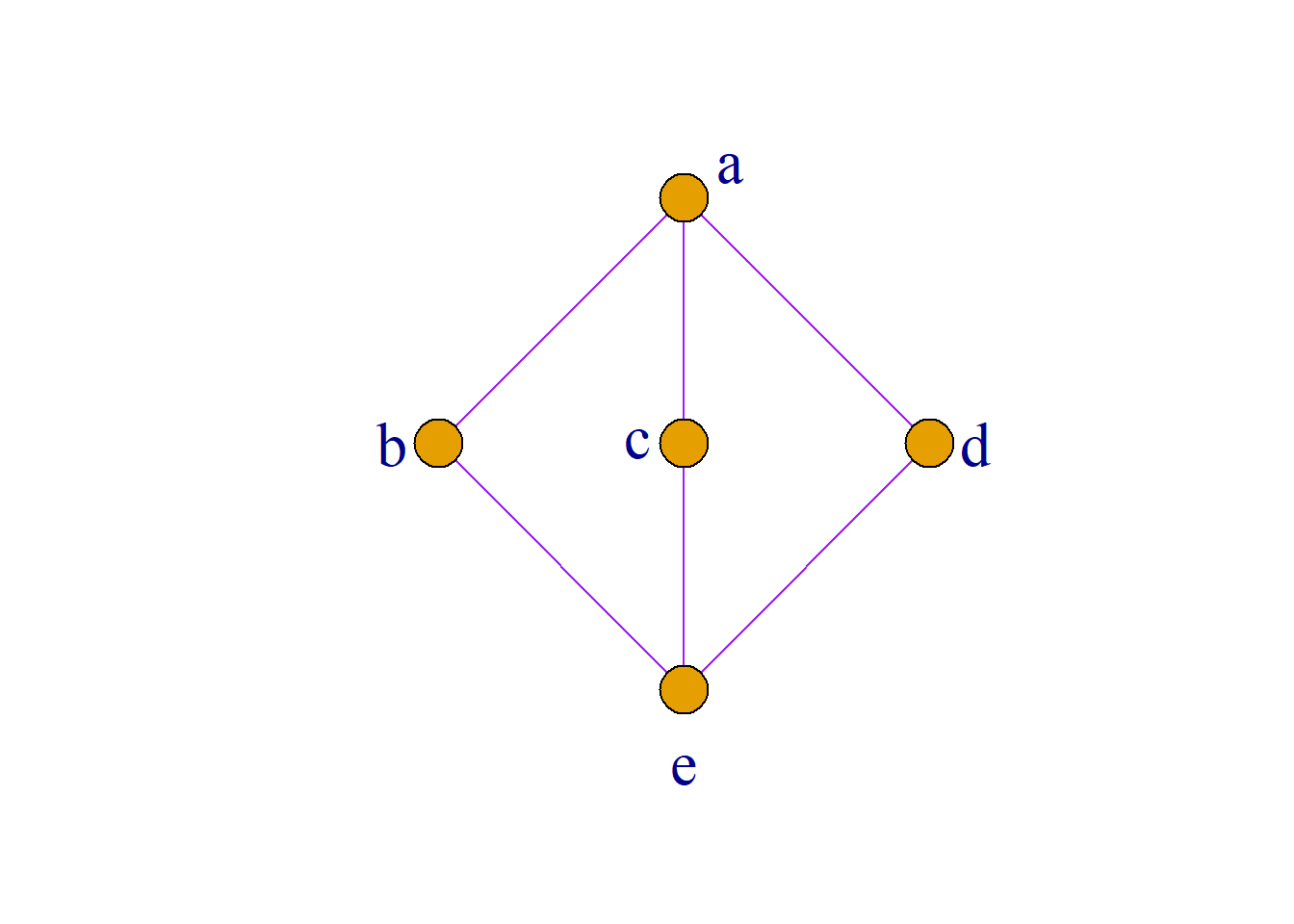
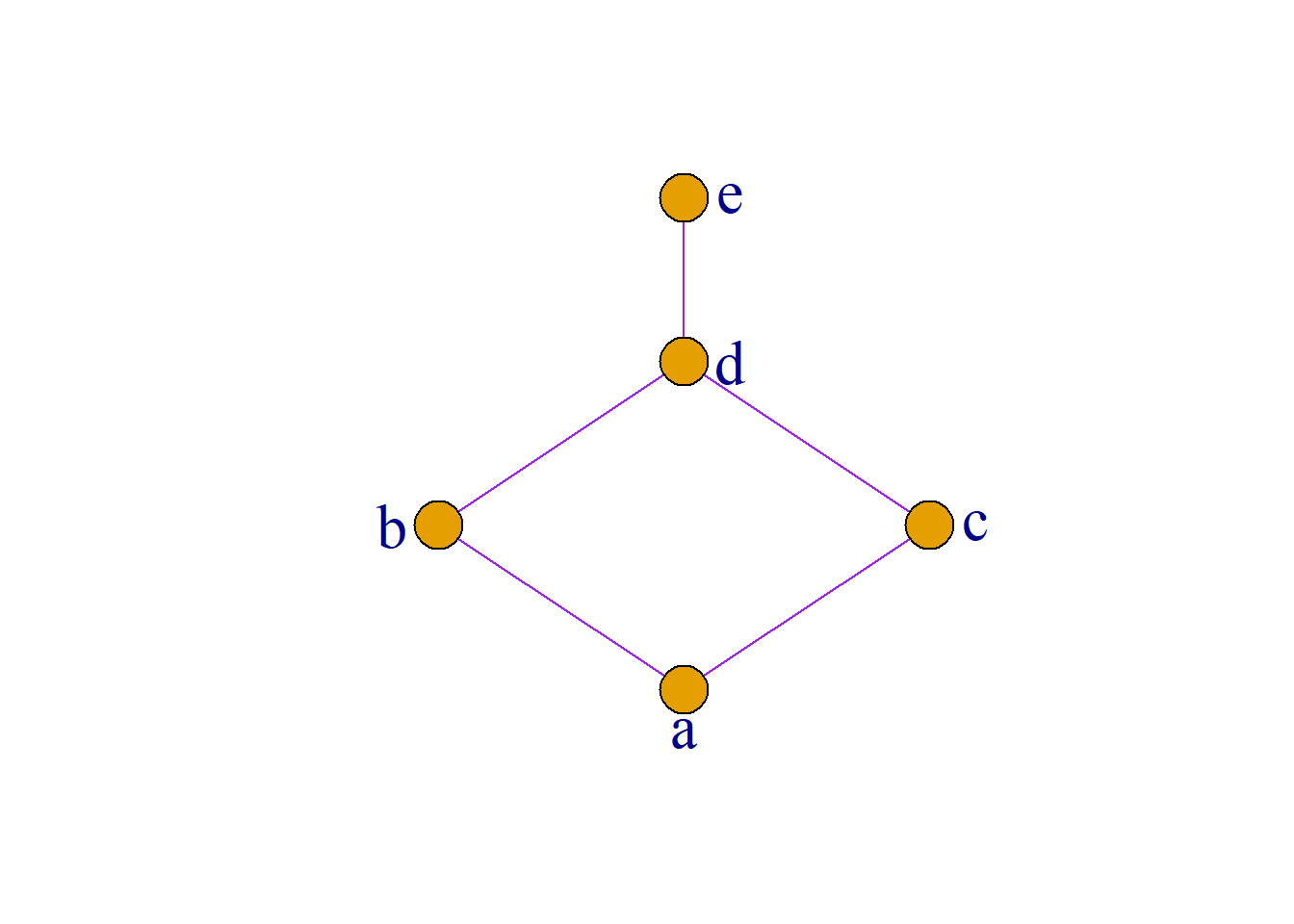
不是分配格的例子(钻石格)：

\[b{\wedge}(c{\vee}d)=b{\wedge}a=b\]

\[(b{\wedge}c){\vee}(b{\wedge}d)=e{\vee}e=e\] 所以:

\[b{\wedge}(c{\vee}d)≠(b{\wedge}c){\vee}(b{\wedge}d)\]

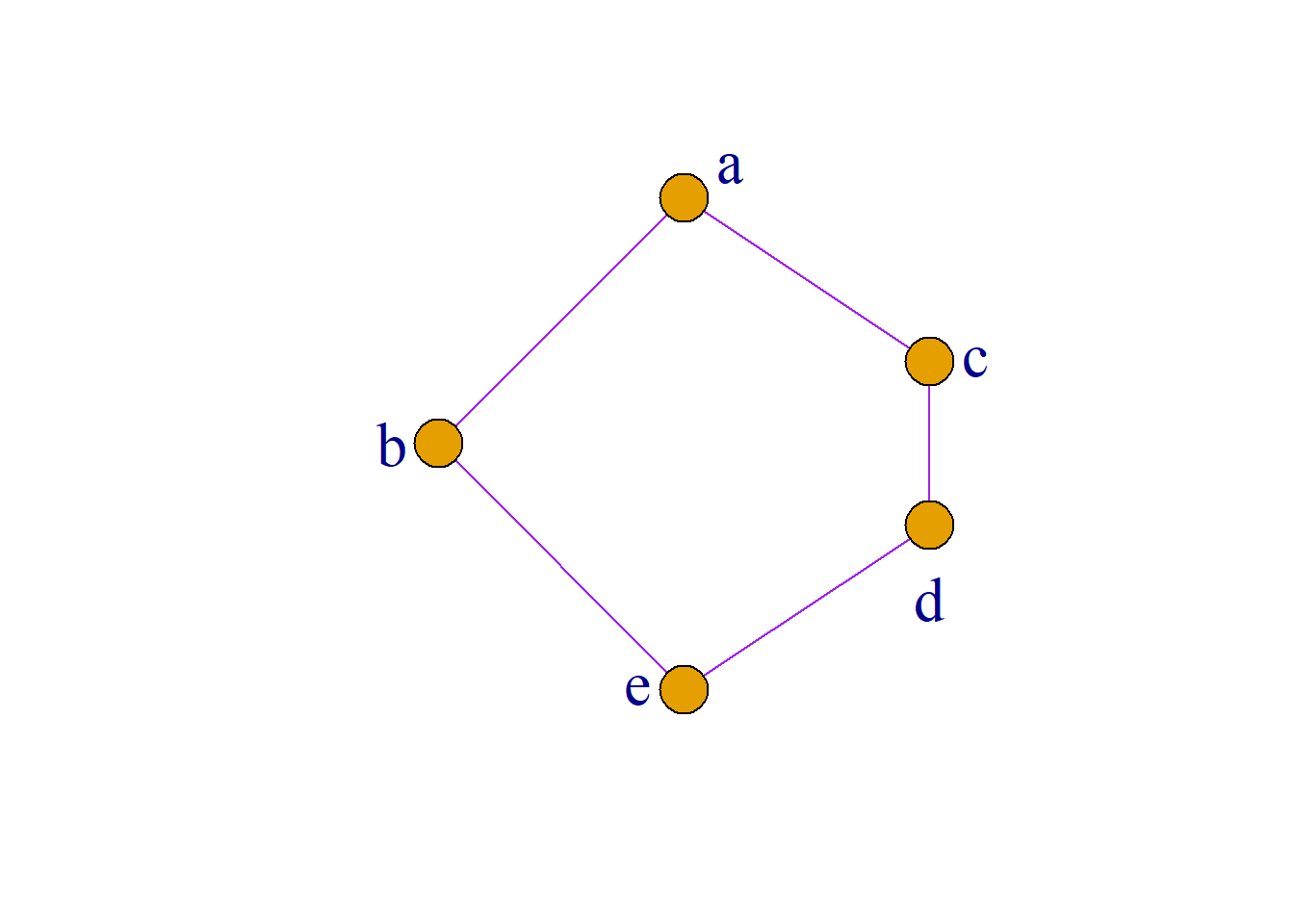
不是分配格的例子(五角格)：

\[c{\wedge}(b{\vee}d)=c{\wedge}a=c\]

\[(c{\wedge}b){\vee}(c{\wedge}d)=e{\vee}d=d\] 所以:

\[c{\wedge}(b{\vee}d){\neq}(c{\wedge}b){\vee}(c{\wedge}d).\]

定理: 在格\({\langle}L, {\vee}, {\wedge}{\rangle}\)中, 如果保交运算\({\wedge}\)运算对保联运算\({\vee}\)是可分配的, 那么, 保联运算\({\vee}\)对保交运算\({\wedge}\)也一定是可分配的. 反之亦然.

证明: 设\(a, b, c\)为格中任意元素, 若 \[a{\wedge}(b{\vee}c)=(a{\wedge}b){\vee}(a{\wedge}c)\] 则 \[(a{\vee}b){\boxed\wedge}(a{\boxed\vee}c)\] \[=((a{\vee}b){\boxed\wedge}a){\boxed\vee}((a{\vee}b){\boxed\wedge}c)\] \[=a{\vee}((a{\boxed\vee}b){\boxed\wedge}c)\] \[=a{\vee}({(a{\boxed\wedge}c){\boxed\vee}(b{\boxed\wedge}c)})\] \[=a{\vee}(b{\wedge}c).\] 另一半同理可证.

定理: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是分配格, 对于任意的\(a, b, c{\in}L\), 若 \(a{\wedge}b=a{\wedge}c, a{\vee}b=a{\vee}c\) 成立, 则\(b=c\).

证明: 因为\((a{\wedge}b){\vee}c=(a{\wedge}c){\vee}c=c\), 而 \[(a{\wedge}b){\vee}c=(a{\vee}c){\wedge}(b{\vee}c)\] \[=(a{\vee}b){\wedge}(b{\vee}c)\] \[=b{\vee}(a{\wedge}c)\] \[=b{\vee}(a{\wedge}b)\] \[=b\] 因此有\(b=c\).

定理: 格\({\langle}L, {\vee}, {\wedge}{\rangle}\)是分配格的充分必要条件是: \({\langle}L, {\vee}, {\wedge}{\rangle}\)中不含有与钻石格和五角格同构的子格.

有补格

定义: 对于格\({\langle}L, {\vee}, {\wedge}{\rangle}\), 若\(L\)中的元素个数有限, 则称\({\langle}L, {\vee}, {\wedge}{\rangle}\)为有限格.

例: 对集合\(S=\{a, b\}\), 则\({\langle}P(S), {\cup}, {\cap}{\rangle}\)是有限格.

因为: \(P(S)=\{\phi, \{a\}, \{b\}, \{a, b\}\}\)是有限集合.

例: 对于格\({\langle}L, {\leq}{\rangle}, {\leq}\)的哈斯图如图所示,

则\({\langle}L, {\leq}{\rangle}\)是有限格.

定义: 对于格\({\langle}L, {\vee}, {\wedge}{\rangle}\), 若存在一个元素\(a{\in}L\), 对于\({\forall}x{\in}L\), 都有\(x{\leq}a(a{\leq}x)\), 则称\(a\)是格\(L\)的一个最大(最小)元.

如果一个格存在最小元和最大元, 则称它们是格的界, 分别用\(\mathbf{0}\)和\(\mathbf{1}\)表示最小元和最大元.

例: 幂集格\({\langle}P(S), {\subseteq}{\rangle} ({\langle}P(S), {\cup}, {\cap}{\rangle})\)存在最大元S, 最小元\(\phi\). 比如: 若\(S=\{a, b\}\), \[P(S)=\{\phi, \{a\}, \{b\}, \{a, b\}\},\,\,\mathbf{1}=\{a, b\}, \mathbf{0} = \phi.\]

定义: 如果一个格同时存在最小元和最大元, 则称该格为有界格.

例: 设\(S=\{2, 3, 4, 5, 6, 7\}\), 对于普通的数之间的小于等于关系\({\leq}, {\langle}S, {\leq}{\rangle}\)构成一个有界格. 其中最小元\(\mathbf{0}=2\), 最大元\(\mathbf{1}=7\).

有限格都是有界格. 如幂集格\({\langle}P(S), {\subseteq}{\rangle}\), \(S=\{a, b\}\) 是有界格.

例: 设\(N\)自然数集, 对于普通的数之间的小于等于关系\({\leq}\), \({\langle}N, {\leq}{\rangle}\)构成一个格.

其中最小元\(\mathbf{0}=0\), 无最大元.不是有界格.

定理: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是有界格, 则对任意的\(a{\in}L\), 必有:

(1)\(a{\vee}\mathbf{1}=\mathbf{1}\), \(a{\wedge}\mathbf{1}=a\); (2)\(a{\vee}\mathbf{0}=a\), \(a{\wedge}\mathbf{0}=\mathbf{0}\).

证明: (1)因\(a{\vee}\mathbf{1}{\in}L\), 所以有\(a{\vee}\mathbf{1}{\leq}\mathbf{1}\). 又因为\(\mathbf{1}{\leq}a{\vee}\mathbf{1}\), 故\(a{\vee}\mathbf{1}=\mathbf{1}\).

因为\(a{\leq}a\), \(a{\leq}\mathbf{1}\), 所以有\(a{\leq}a{\wedge}\mathbf{1}\). 又因为\(a{\wedge}\mathbf{1}{\leq}a\), 故\(a{\wedge}\mathbf{1}=a\). (2) 可以类似地证明.

定义: 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是有界格, 对于\(L\)中的一元素\(a\).

若存在\(b{\in}L\), 使得\(a{\vee}b=\mathbf{1}\), \(a{\wedge}b=\mathbf{0}\), 则称\(b\)为\(a\)的补元.

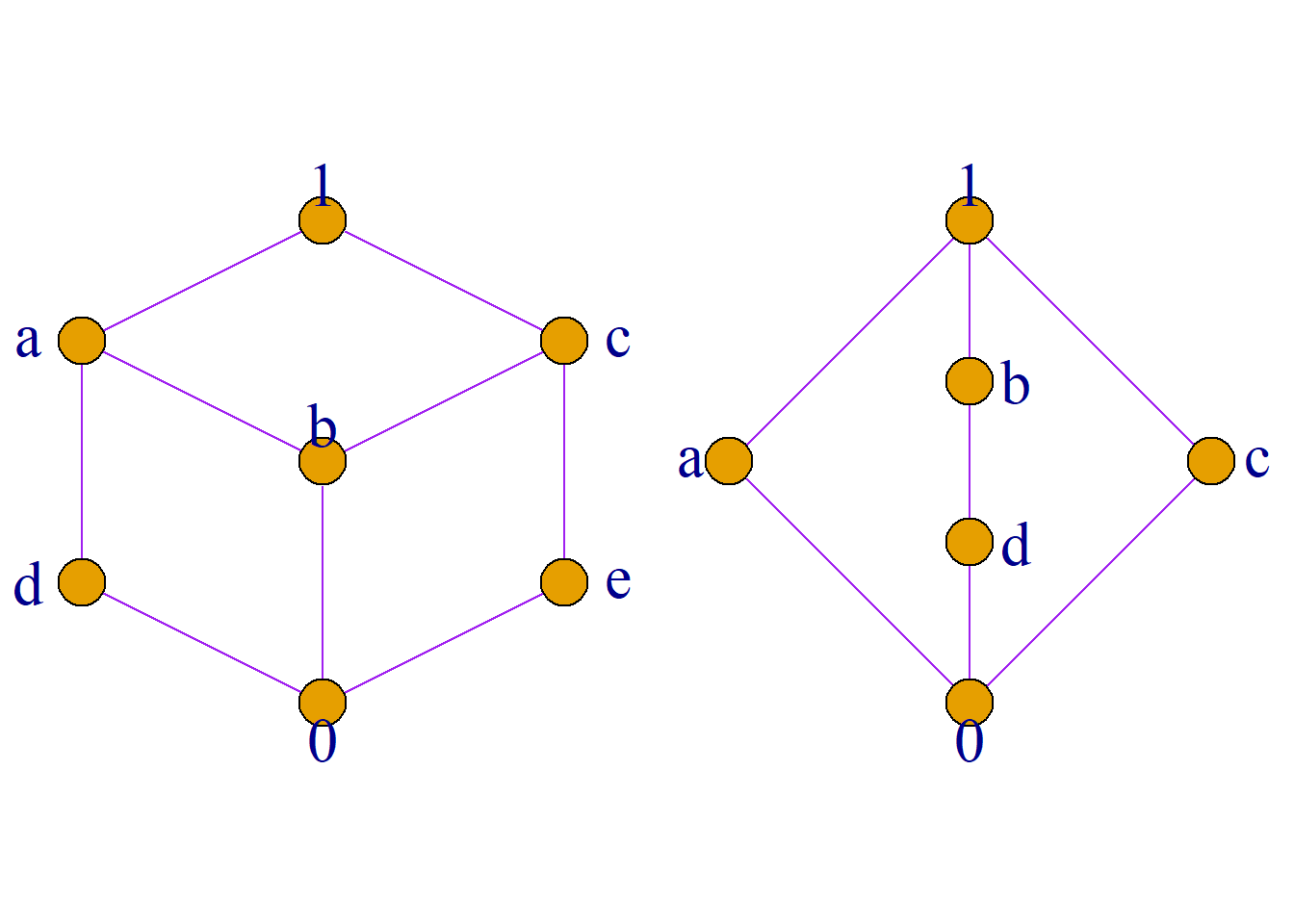
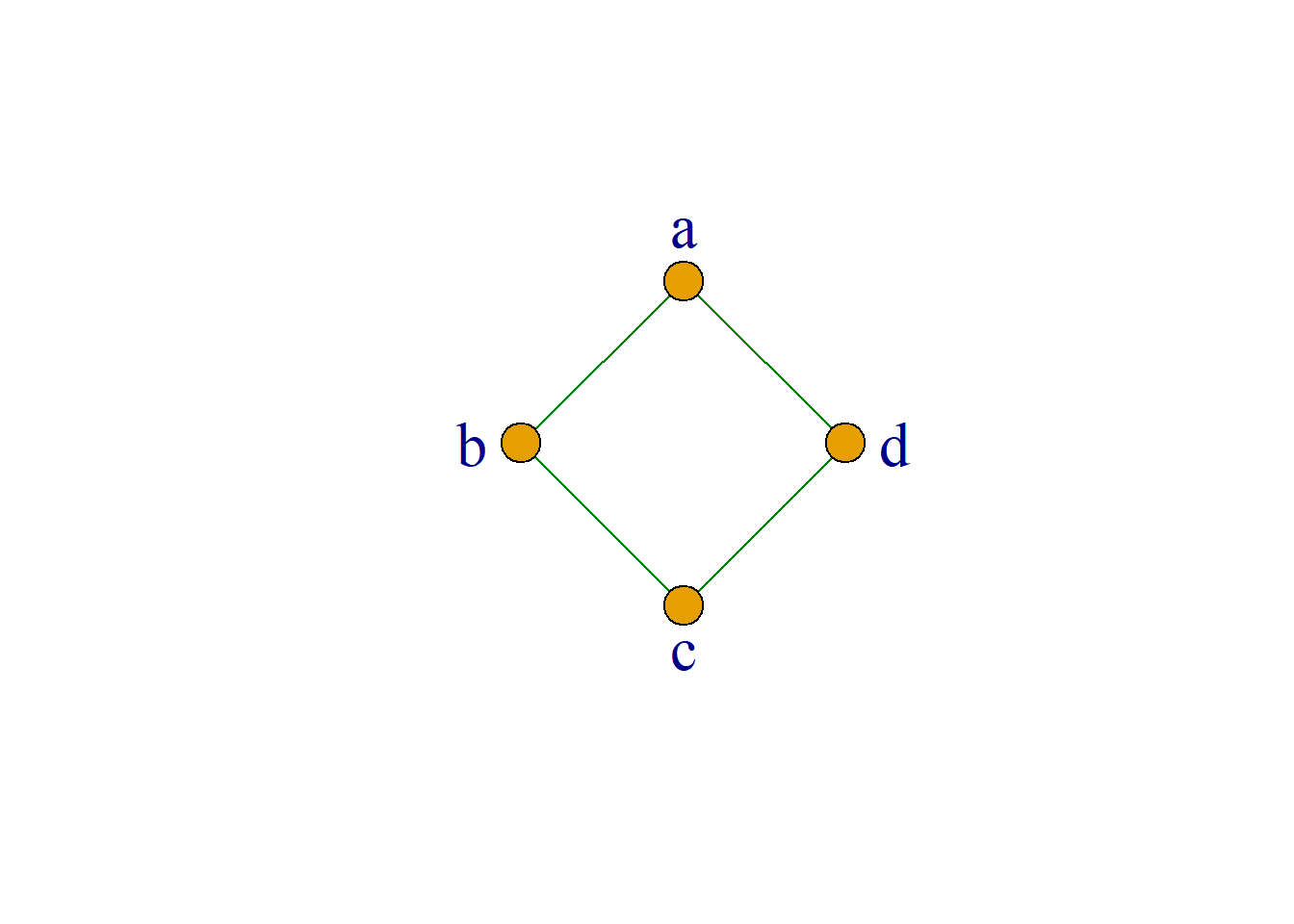
在左图中, \(\mathbf{1}\)和\(\mathbf{0}\)互补; \(a\)的补元是\(e\);

\(b\)无补元;\(c\)的补元是\(d\); \(d\)的补元是\(c\)和\(e\);

\(e\)的补元是\(a\)和\(d\).

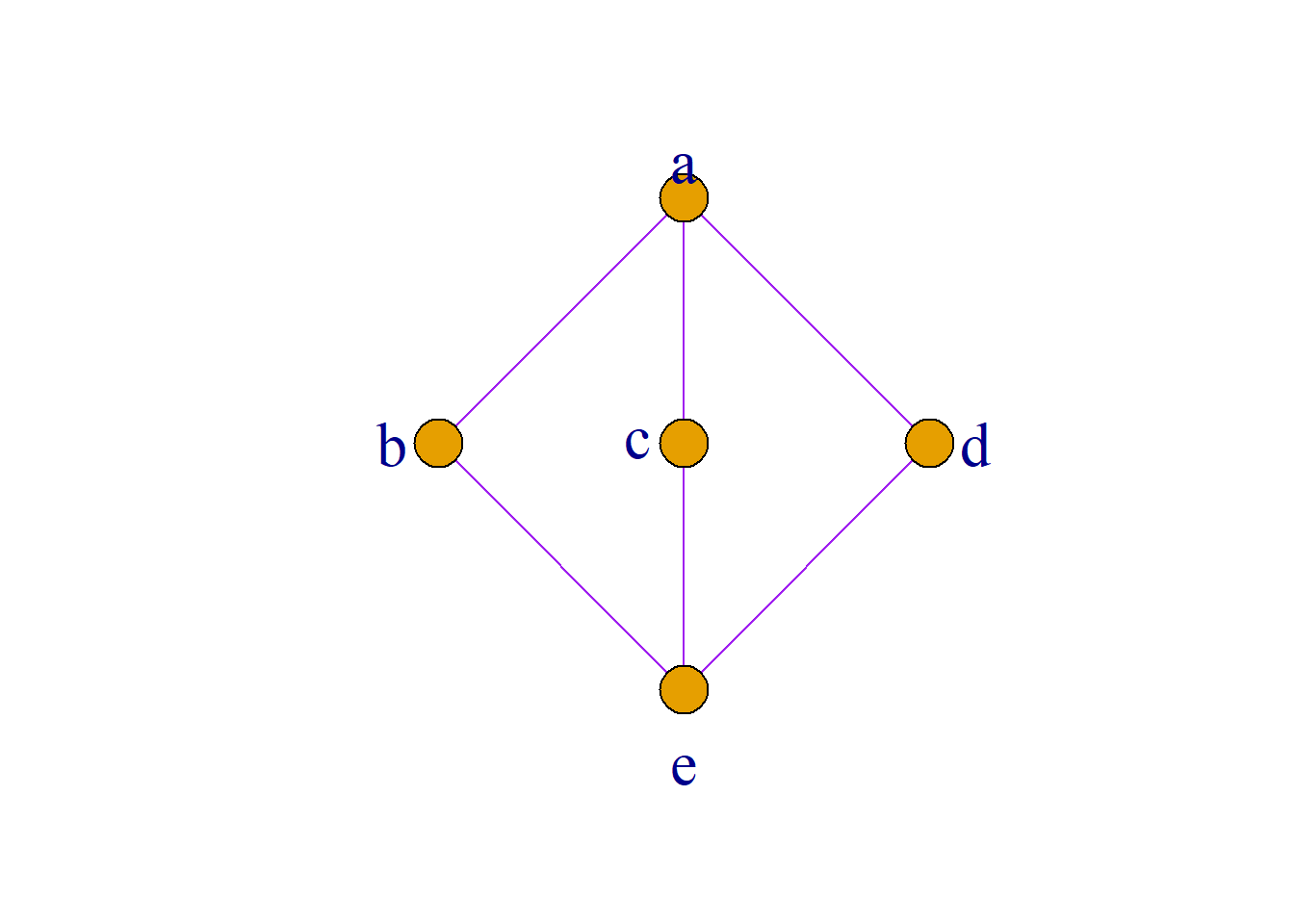
在右图中, \(\mathbf{1}\)和\(\mathbf{0}\)互补; \(a\)的补元是\(b\), \(c\)和\(d\);

\(b\)的补元是\(a\)和\(c\); \(c\)的补元是\(a\), \(b\)和\(d\);

\(d\)的补元是\(a\)和\(c\).

补元有下列特点:

补元是相互的, 即\(b\)是\(a\)的补元, 那么\(a\)也是\(b\)的补元;
\(\mathbf{0}\)和\(\mathbf{1}\)互为补元;
并非有界格中每个元素都有补元, 即使存在也未必是唯一的.

定义: 在一个有界格\({\langle}L, {\vee}, {\wedge}{\rangle}\)中, 如果\(L\)中每个元素都有补元素, 则称此格为有补格.

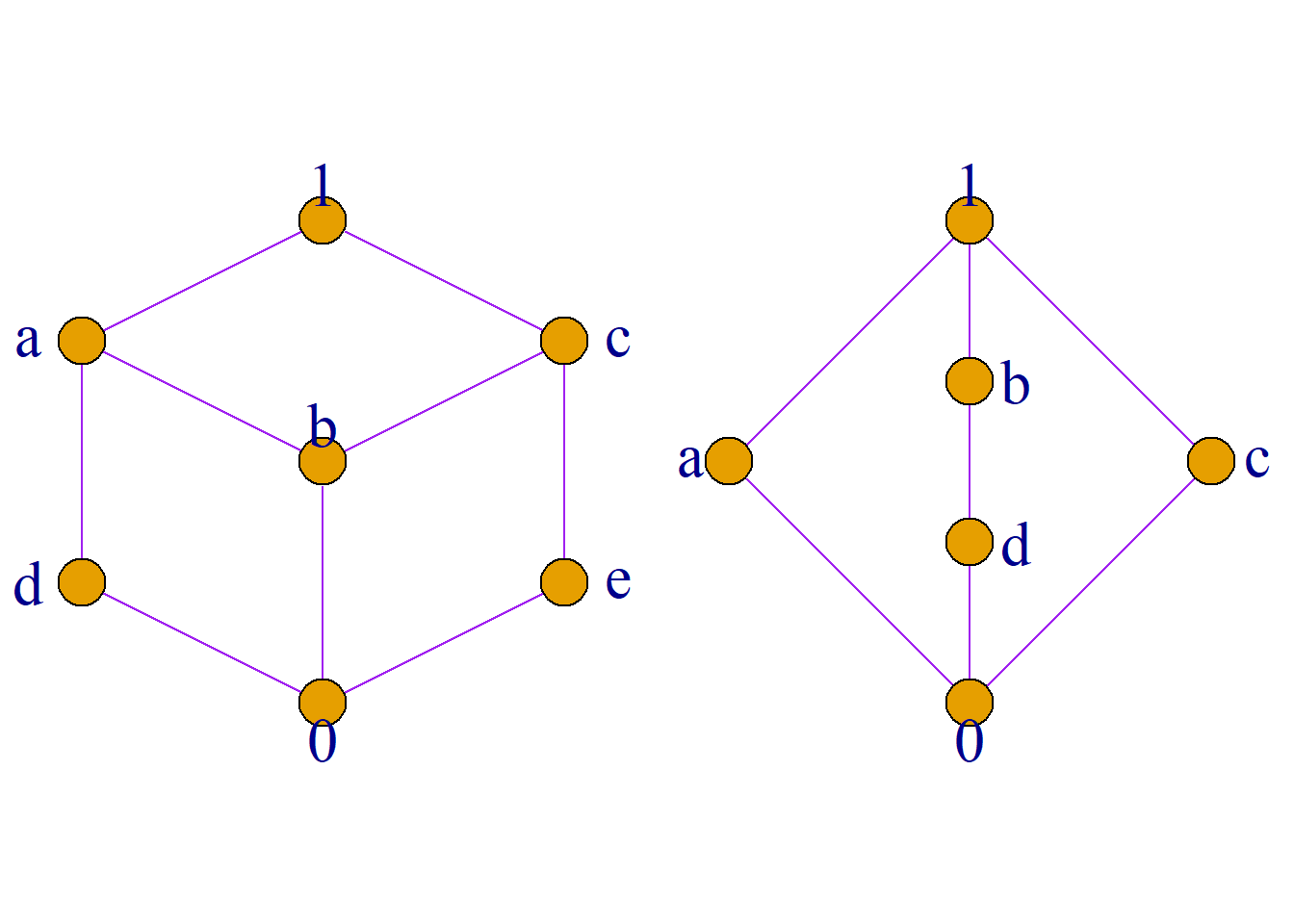
定理: 有补格\({\langle}L, {\vee}, {\wedge}{\rangle}\)中元素\(\mathbf{0}\)和\(\mathbf{1}\)的补元是唯一的.

定义: 如果一个格既是有补格又是分配格, 则称它为有补分配格.

例: 设\(S\)是一个非空有限集, 则\({\langle}P(S), {\cup}, {\cap}{\rangle}\)就是一个有补分配格.

因为\(\mathbf{1}= S\), \(\mathbf{0}=\phi\), 且对于任意\(A{\in}P(S)\) (\(A{\subseteq}S\)), 都有唯一的补元素\({\sim}A=S-A{\in}P(S)\) (\({\sim}A{\subseteq}S\)), \(A\)的补集就是\(A\)的补元. \(A{\cup}{\sim}A=S\), \(A{\cap}{\sim}A=\phi\).

定理: 有补分配格中每一元素的补元都是唯一的.

证明(反证法): 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是有补分配格, \(a\)是\(L\)中的一元素, 假设它有两个补元\(b\)和\(c\), 那么:

\[a{\vee}b=\mathbf{1},\,\, a{\wedge}b=\mathbf{0},\,\,a{\vee}c=\mathbf{1},\,\, a{\wedge}c=\mathbf{0}\]

即: \(a{\vee}b=a{\vee}c\), \(a{\wedge}b=a{\wedge}c\).

根据分配格的性质, 有\(b=c\). 所以\(a\)的补元是唯一的.

有补分配格中任一元素\(a\)的唯一补元可用\({\sim}a\)(或\(a^\prime\))来表示.

定理: 对有补分配格中每一元素\(a\), 有\((a^{\prime})^{\prime}=a\).(对合律)

证明:因为\(a{\vee}a^{\prime}=\mathbf{1}, a{\wedge}a^{\prime}=\mathbf{0}\), 由交换律知: \(a^{\prime}{\vee}a=\mathbf{1}, a^{\prime}{\wedge}a=\mathbf{0}\), 所以, \(a ^{\prime}\)的补元是\(a\), 由补元的唯一性有\((a^{\prime})^{\prime}=a\).

定理 (德·摩根律): 设\({\langle}L, {\vee}, {\wedge}{\rangle}\)是有补分配格, 则对\(L\)中任意元素\(a\)和\(b\), 有

\((a{\vee}b)^{\prime}= a^{\prime}{\wedge}b^{\prime}\)
\((a{\wedge}b)^{\prime}= a^{\prime}{\vee}b^{\prime}\)

证明:(1) 由分配律可知:

\[(a{\vee}b){\vee}(a^{\prime}{\wedge}b^{\prime})=\] \[(a{\vee}b{\vee}a^{\prime}){\wedge}(a{\vee}b{\vee}b^{\prime}) =\mathbf{1}{\wedge}\mathbf{1}=\mathbf{1}\]

\[(a{\vee}b){\wedge}(a^{\prime}{\wedge}b^{\prime})=\] \[(a{\wedge}a^{\prime}{\wedge}b^{\prime}){\vee}(b{\wedge}a^{\prime}{\wedge}b^{\prime}) =\mathbf{0}{\vee}\mathbf{0}=\mathbf{0}\]

由补元的唯一性可得\((a{\vee}b)^{\prime}= a^{\prime}{\wedge}b^{\prime}\). 同理可证(2)式.

定理: 对有补分配格的任何元素\(a\)和\(b\), 有: \(a{\leq}b{\Leftrightarrow}a{\wedge}b^{\prime}=\mathbf{0}{\Leftrightarrow}a^{\prime}{\vee}b=\mathbf{1}\).

证明: \[a{\leq}b{\Rightarrow}a{\wedge}b^{\prime}=(a{\wedge}b^{\prime}){\vee}(b{\wedge}b^{\prime})=(a{\vee}b){\wedge}b^{\prime}=b{\wedge}b^{\prime}=\mathbf{0}.\] 反过来， \[a{\wedge}b^\prime=\mathbf{0}{\Leftrightarrow}(a{\wedge}b^\prime)^\prime=a^\prime{\vee}b=\mathbf{1}\] \[{\Rightarrow}a{\vee}b=(a{\vee}b)\wedge(a^\prime{\vee}b)=(a{\wedge}a^\prime){\vee}b=b{\Rightarrow}a{\leq}b.\]

定义: 一个有补分配格称为布尔代数.

在有补分配格中, 因为每一个元素\(a\)都有唯一的补元\(a^{\prime}\), 所以可定义一个一元运算\(^{\prime}\), 使得\(a^{\prime}\)为\(a\)的补元, 这个一元运算称为补运算.

布尔代数一般用\({\langle}B, {\vee}, {\wedge}, ^{\prime}{\rangle}\)或\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)来表示.

例如, 布尔代数: \[{\langle}P(S), {\cup}, {\cap}, {\sim}{\rangle}或{\langle}P(S), {\cup}, {\cap}, {\sim}, \phi, S {\rangle}.\]

定义: 具有有限个元素的布尔代数称为有限布尔代数.

定义: 设\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)是布尔代数, \(A{\subseteq}B\)且非空, 若\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)也是布尔代数, 则称\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)是\({\langle}B, {\vee}, {\wedge}, ^{\prime}, 0, 1{\rangle}\)的子(布尔)代数.

定理: 设\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)为布尔代数, \(A{\subseteq}B\)且\(A\)含有元素\(\mathbf{0}\)和\(\mathbf{1}\), 若\(A\)对运算\({\vee}\), \({\wedge}\)和\(^\prime\)封闭, 那么\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)为\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)的子代数.

定义: 设\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)和\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)是两个布尔代数, 如果存在\(A\)到\(B\)的函数\(f\), 使得对于任意的\(a, b{\in}A\), 都有: \[f(a{\vee}b)=f(a){\vee}f(b)\] \[f(a{\wedge}b)=f(a){\wedge}f(b)\] \[f(a^{\prime})=(f(a))^{\prime}\] 则称\(f\)是布尔代数\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)到布尔代数\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)的同态(映射).

若\(f\)是单射的, 则称为单同态;

若\(f\)是满射的, 则称为满同态;

若\(f\)是双射的, 则称为同构;

若存在同构映射f, 则称布尔代数\({\langle}A, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)和布尔代数\({\langle}B, {\vee}, {\wedge}, ^{\prime}, \mathbf{0}, \mathbf{1}{\rangle}\)同构.

例: 设\(U={\langle}K, {\vee}, {\wedge}, {\sim}, \mathbf{0}_K, \mathbf{1}_K{\rangle}\)和\(V={\langle}L, {\cup}, {\cap}, -, \mathbf{0}_L, \mathbf{1}_L{\rangle}\)是两个布尔代数, 并设\(f\)是从\(U\)到\(V\)的同态映射. 即对任意的\(a, b{\in}K\), 有 \[f(a{\vee}b)=f(a){\cup}f(b),\,\,f(a{\wedge}b)=f(a){\cap}f(b),\,\,f({\sim}a)=-f(a).\] 试证明: \(f(\mathbf{0}_K)=\mathbf{0}_L\), \(f(\mathbf{1}_K)=\mathbf{1}_L\).

证明: 因为\(\mathbf{0}_K, \mathbf{1}_K{\in}K\), \(\mathbf{0}_L, \mathbf{1}_L{\in}L\), 所以: \[f(\mathbf{0}_K), f(\mathbf{1}_K){\in}L,\,\,f(\mathbf{0}_K)=f({\sim}\mathbf{1}_K)=-f(\mathbf{1}_K),\,\,f(\mathbf{1}_K)=f({\sim}\mathbf{0}_K)=-f(\mathbf{0}_K)\] 可见\(f(\mathbf{0}_K)\)和\(f(\mathbf{1}_K)\)互补. 所以: \(f(\mathbf{0}_K){\cup}f(\mathbf{1}_K)=\mathbf{1}_L,\,\,f(\mathbf{0}_K){\cap}f(\mathbf{1}_K)=\mathbf{0}_L\).

又: \[f(\mathbf{1}_K)=f(\mathbf{0}_K{\vee}\mathbf{1}_K)=f(\mathbf{0}_K){\cup}f(\mathbf{1}_K)=\mathbf{1}_L\] \[f(\mathbf{0}_K)=f(\mathbf{0}_K{\wedge}\mathbf{1}_K)=f(\mathbf{0}_K){\cap}f(\mathbf{1}_K)=\mathbf{0}_L\] 所以: \(f(\mathbf{1}_K)=\mathbf{1}_L,\,\,f(\mathbf{0}_K)=\mathbf{0}_L\).