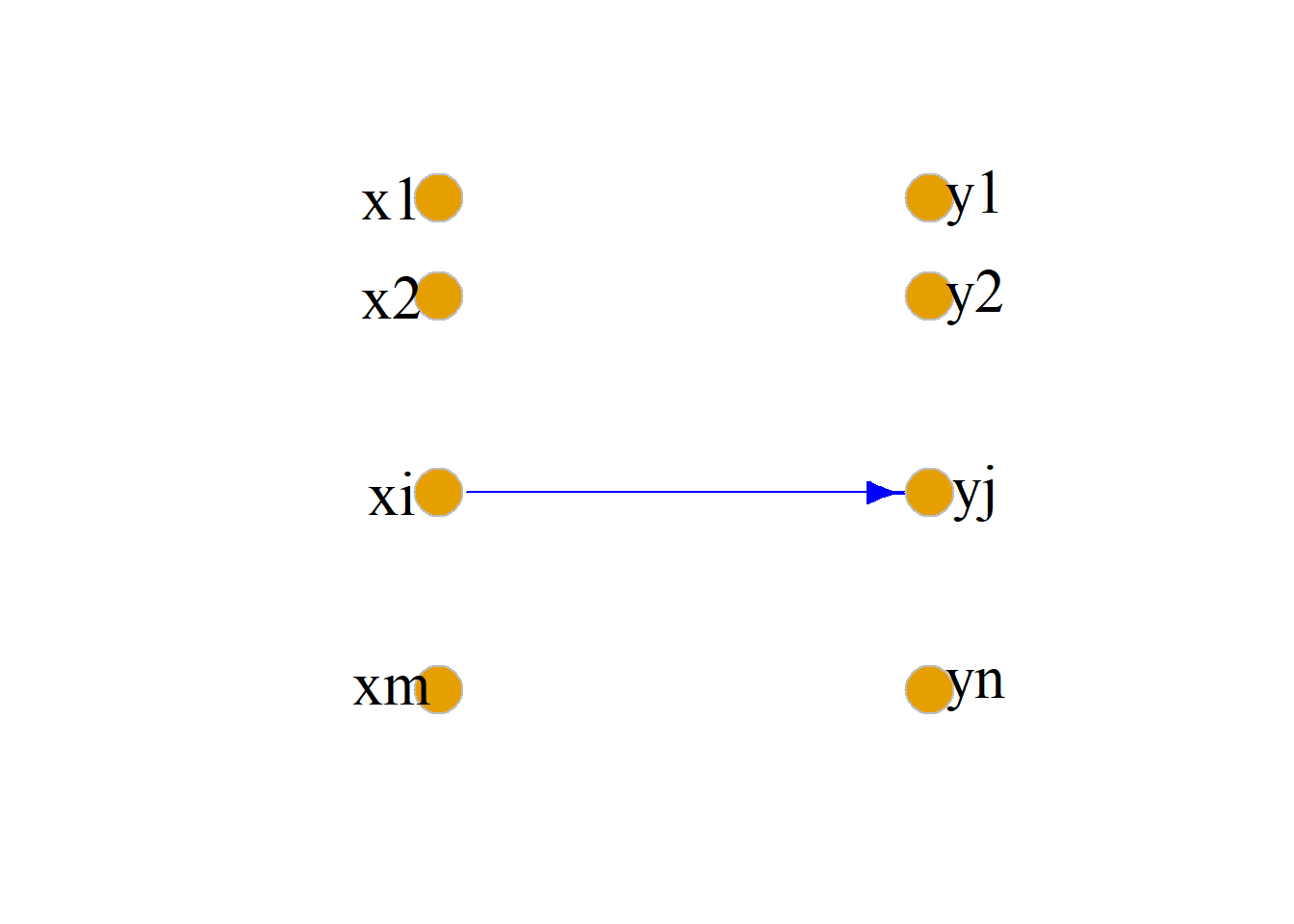
关系

主讲教师

李辉

关系的概念在现实世界中是普遍存在的.

如: 兄弟关系、同学关系、同事关系、数的大小关系、集合间的包含关系等等.

集合论为刻画此类关系提供了一种数学模型: 关系(Relation).

关系也是一个集合, 以具有相应关系的对象组合为其元素.

序偶与笛卡尔乘积

定义: 由两个具有给定次序的\(x\)和\(y\)所组成的序列称为序偶(Ordered Pair), 记作\({\langle}x, y\rangle\). 其中, \(x\)称为第1元素(分量), \(y\)称为第2元素(分量).

例: 在笛卡尔坐标系中, 2维平面上1个点的坐标\(\langle x, y\rangle\) 就是1个序偶.

这里特别强调的是次序:

当\(x\neq y\)时, \(\langle x, y\rangle\neq\langle y, x\rangle\)
\(\langle x, y\rangle=\langle u, v\rangle\)的充分必要条件是: \(x=u, y=v\)

定义: 由\(n\)个具有给定次序的个体\(a_1, a_2, \cdots, a_n\)组成的序列, 称为有序\(n\)元组. 记作: \(\langle a_1, a_2, \cdots, a_n\rangle\).

其中\(a_i\)称为第\(i\)个分量.

\[\langle a_1, a_2, \cdots, a_n\rangle=\langle b_1, b_2, \cdots, b_n\rangle\]

当且仅当

\[a_i=b_i\, (i=1, 2, \cdots, n).\]

定义: 设\(A, B\)是任意两个集合, 用\(A\)中元素为第1元, \(B\)中元素为第2元构成序偶.

这样的序偶组成的集合称为\(A\)和\(B\)的笛卡尔积(Cartesian Product).

符号化: \(A\times B=\{\langle x, y\rangle |x\in A, y\in B\}.\)

例: 设\(A=\{a, b\}, B=\{0, 1, 2\}, C=\Phi\), 则

\[A\times B=\{\langle a, 0\rangle, \langle a, 1\rangle, \langle a, 2\rangle, \langle b, 0\rangle, \langle b, 1\rangle, \langle b, 2\rangle\}\] \[B\times A=\{\langle 0, a\rangle, \langle 0, b\rangle, \langle 1, a\rangle, \langle 1, b\rangle, \langle 2, a\rangle, \langle 2, b\rangle\}\] \[A\times A=\{\langle a, a\rangle, \langle a, b\rangle, \langle b, a\rangle, \langle b, b\rangle\}\] \[B\times B=\{\langle 0, 0\rangle, \langle 0, 1\rangle, \langle 0, 2\rangle, \langle 1, 0\rangle, \langle 1, 1\rangle, \langle 1, 2\rangle, \langle 2, 0\rangle, \langle 2, 1\rangle, \langle 2, 2\rangle\}\] \[A\times C=\Phi\] \[C\times A=\Phi\]

显然, \(A\times B\neq B\times A\), 故笛卡儿乘积不满足交换律.

例: 花色 \(\times\) 大小:

\[\{(\spadesuit, A), (\spadesuit, K), (\spadesuit, Q), (\spadesuit, J), (\spadesuit, 10), \cdots, (\diamondsuit, 6), (\diamondsuit, 5), (\diamondsuit, 4), (\diamondsuit, 3), (\diamondsuit, 2)\}.\]

由排列组合的知识可知: 如果\(|A|=m\), \(|B|=n\), 则\(|A\times B|=mn\).

定义: 设\(A_1, A_2, \cdots, A_n\)是任意给定的\(n\)个集合, 若有序\(n\)元组\(\langle a_1, a_2, \cdots, a_n\rangle\)的第1元取自集合\(A_1\), 第2元取自\(A_2\), \(\cdots\), 第\(n\)元取自\(A_n\), 则由所有这样的有序\(n\)元组组成的集合称为集合\(A_1, A_2, \cdots, A_n\)的笛卡儿积, 并用\(A_1\times A_2\times\cdots\times A_n\)表示. 即 \[A_1\times A_2\times\cdots\times A_n=\{\langle a_1, a_2, \cdots, a_n\rangle |a_i\in A_i, i=1, 2, \cdots, n\}\]

例: 设\(A=\{1\}, B=\{a, b\}, C=\{x, y\}\), 则:

\[A\times B=\{\langle 1, a\rangle, \langle 1, b\rangle\}\] \[B\times C=\{\langle a, x\rangle, \langle b, x\rangle, \langle a, y\rangle, \langle b, y\rangle\}\] \[(A\times B)\times C =\{\langle\langle 1, a\rangle, x\rangle, \langle\langle 1, a\rangle, y\rangle, \langle\langle 1, b\rangle, x\rangle, \langle\langle 1, b\rangle, y\rangle\} \] \[A\times (B\times C) =\{\langle 1, \langle a, x\rangle\rangle, \langle 1, \langle a, y\rangle\rangle, \langle 1, \langle b, x\rangle\rangle, \langle 1, \langle b, y\rangle\rangle\}\]

显然, 笛卡尔乘积不满足结合律.

下列分配律成立:

\(A\times (B\cup C)=(A\times B)\cup (A\times C)\)
\(A\times (B\cap C)=(A\times B)\cap (A\times C)\)
\((A\cup B)\times C=(A\times C)\cup (B\times C)\)
\((A\cap B)\times C=(A\times C)\cap (B\times C)\)
\(A\times (B-C)=(A\times B)-(A\times C)\)
\((A-B)\times C=(A\times C)-(B\times C)\)

若\(C\neq\Phi\), 则 \[A\subseteq B\Leftrightarrow (A\times C\subseteq B\times C)\Leftrightarrow (C\times A\subseteq C\times B)\]

设\(A, B, C, D\)是四个非空集合, 则 \[A\times B\subseteq C\times D\] 当且仅当 \[A\subseteq C \wedge B\subseteq D.\]

证明分配律: \(A\times (B\cup C)=(A\times B)\cup (A\times C)\).

证明: 对任意的\(\langle x, y\rangle\), \(\langle x, y\rangle\in A\times (B\cup C)\), 则: \[x\in A\wedge y\in (B\cup C)\] \[x\in A\wedge (y\in B\vee y\in C)\] \[(x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\] \[\langle x, y\rangle\in A\times B\vee \langle x, y\rangle\in A\times C\] \[\langle x, y\rangle\in (A\times B)\cup (A\times C)\] 所以\(A\times (B\cup C)\subseteq(A\times B)\cup (A\times C)\)

对任意的\(\langle x, y\rangle\), \(\langle x, y\rangle\in (A\times B)\cup (A\times C)\), \[\langle x, y\rangle\in A\times B\vee \langle x, y\rangle\in A\times C\] \[(x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\] \[x\in A\wedge (y\in B\vee y\in C)\] \[x\in A\wedge y\in (B\cup C)\] \[\langle x, y\rangle\in A\times (B\cup C)\] 所以\((A\times B)\cup (A\times C) \subseteq A\times (B\cup C)\)

综上:\[A\times (B\cup C)=(A\times B)\cup (A\times C).\]

例: 设\(A, B, C\)是三个任意集合且\(C\neq\Phi\), 则 \(A\subseteq B\)当且仅当\(A\times C\subseteq B\times C\).

证明: (必要性)设\(A\subseteq B\), 任取\(x\in A\), 则\(x\in B\).

对任意的\(\langle x, y\rangle\), 若\(\langle x, y\rangle\in A\times C\), 则: \[x\in A\wedge y\in C\] \[x\in B\wedge y\in C\] \[\langle x, y\rangle\in B\times C\] 所以\[A\times C\subseteq B\times C.\]

(充分性)设\(A\times C\subseteq B\times C\).

因\(C\neq\Phi\), 故存在\(y\in C\). 任取\(x\in A\), 则 \[x\in A\wedge y\in C\] \[\langle x, y\rangle\in A\times C\] \[\langle x, y\rangle\in B\times C\] \[x\in B\wedge y\in C\] \[x\in B\] 所以\(A\subseteq B\).

故 \(A\subseteq B\)当且仅当\(A\times C\subseteq B\times C\).

关系及其表示

关系的定义

定义: 如果一个集合的全部元素都是序偶, 则称这个集合为一个二元关系, 记作R.

例: 设\(A=\{2, 3, 4\}\), 定义: \[R_1=\{\langle x, y\rangle |x, y\in A \wedge x> y\}\] \[R_2=\{\langle x, y\rangle |x, y\in A \wedge x\geq y\}\] 即: \[R_1=\{\langle 4, 3\rangle, \langle 4, 2\rangle, \langle 3, 2\rangle\}\] 表示集合\(A\)上元素的大于关系. \[R_2=\{\langle 4, 4\rangle, \langle 4, 3\rangle, \langle 4, 2\rangle, \langle 3, 3\rangle, \langle 3, 2\rangle, \langle 2, 2\rangle\}\] 表示集合\(A\)上元素的大于等于关系.

定义: 设\(A, B\)是任意两个集合, \(A\times B\)的任意一个子集所定义的二元关系\(R\)称为从集合\(A\)到集合\(B\)的一个二元关系.

当\(A=B\)时, 称\(R\)为\(A\)上的二元关系.

例: 设\(A=\{1, 2, 3\}, B=\{a, b\}\), 则 \[A\times B=\{\langle 1, a\rangle, \langle 1, b\rangle, \langle 2, a\rangle, \langle 2, b\rangle, \langle 3, a\rangle, \langle 3, b\rangle \}\] \(A\times B\)的任一子集都是一个关系. 如: \[R_1=\{\langle 1, a\rangle, \langle 1, b\rangle \}\] \[R_2=\{\langle 1, a\rangle, \langle 2, a\rangle, \langle 3, b\rangle \}\] 等都是从\(A\)到\(B\)的二元关系.

一般地, 在\(n\)个集合上可以定义\(n\)元关系.

定义: 设\(A_1, A_2, \cdots, A_n\)是任意给定的集合, 笛卡儿积\(A_1\times A_2\times\cdots\times A_n\)的任意一个子集\(R\)称为\(A_1, A_2, \cdots, A_n\)上的一个\(n\)元关系.

当\(A_1=A_2=\cdots=A_n=A\)时, 称\(R\)为\(A\)上的\(n\)元关系.

例: 设\(A, B\)是任意两个集合, 若\(|A|=m, |B|=n\), 问从集合\(A\)到集合\(B\)共有多少个不同的二元关系？

解: 由于笛卡尔积\(A\times B\)的任何一个子集都是从\(A\)到\(B\)的二元关系, 而 \[|A\times B|=m\times n\] \[|P(A\times B)|=2^{m\times n}\] 所以, 从集合\(A\)到集合\(B\)共有\(2^{m\times n}\)个不同的二元关系.

例: 设\(A=\{0, 1\}, B=\{2\}\)是任意两个集合, 则

\[A\times B=\{\langle 0, 2\rangle, \langle 1, 2\rangle\}\]

所以\(|A\times B|=2\times 1=2, |P(A\times B)|=2^2=4.\)

从集合\(A\)到集合\(B\)共有4个不同的二元关系. 包括: \[R_1=\Phi,\,\,R_2=\{\langle 0, 2\rangle\},\,\,R_3=\{\langle 1, 2\rangle\},\,\,R_4=\{\langle 0, 2\rangle, \langle 1, 2\rangle\}.\]

例: 设\(A=\{a, b, c\}\), \(A\)上可定义多少个二元关系？

解: 因为\(|A|=3\), 所以\(|A\times A|=3\times 3=9\), \(|P(A\times A)|=2^9=512\).

\(A\)上可定义512个二元关系.

定义: 设\(R\)是从集合\(A\)到集合\(B\)的一个二元关系。

则由\(R\)中所有序偶的第1元组成的集合称为\(R\)的定义域, 记作domR(或\(D(R)\)).

由\(R\)中所有序偶的第2元组成的集合称为\(R\)的值域, 记作ranR(或\(V(R)\)). 即: \[D(R)=\{x|x\in A\wedge\langle x, y\rangle\in R\}\] \[V(R)=\{y|y\in B\wedge\langle x, y\rangle\in R\}\] 显然, \(D(R)\subseteq A, V(R)\subseteq B\).

例: 设\(A=\{1, 2, 3, 4\}\), 求\(A\)上的小于关系及相应的定义域和值域.

解: 小于关系:\[R=\{\langle 1, 2\rangle, \langle 1, 3\rangle, \langle 1, 4\rangle, \langle 2, 3\rangle, \langle 2, 4\rangle, \langle 3, 4\rangle\}, \]

\[D(R)=\{1, 2, 3\}, V(R)=\{2, 3, 4\}.\]

例: 设\(X=\{a, b, c, d, e, f\}\), \(X\)上的二元关系: \[R=\{\langle a, b\rangle, \langle c, d\rangle, \langle e, f\rangle\}, \] 求\(R\)的定义域和值域.

解: \(D(R)=\{a, c, e\}\), \(V(R)=\{b, d, f\}.\)

几种常见的二元关系: 设\(A\)是任意集合, 则:

\(R_A=\Phi\), 称作\(A\)上的空关系
\(E_A=\{\langle x, y\rangle |x, y\in A\}\), 称作\(A\)上的全域关系
\(I_A=\{\langle x, x\rangle |x\in A\}\), 称作\(A\)上的恒等关系
\(D_A=\{\langle x, y\rangle |x, y\in A\wedge x|y\}\), 称作\(A\)上的整除关系
\(L_A=\{\langle x, y\rangle |x, y\in A\wedge x\leq y\}\), 称作\(A\)上的小于等于关系
\(L_{A^\prime}=\{\langle x, y\rangle |x, y\in A\wedge x<y\}\), 称作\(A\)上的小于关系

例: 设\(X=\{1, 2, 3\}\), \(E_X=\{\langle 1, 1\rangle, \langle 1, 2\rangle, \langle 1, 3\rangle, \langle 2, 1\rangle, \langle 2, 2\rangle, \langle 2, 3\rangle, \langle 3, 1\rangle, \langle 3, 2\rangle, \langle 3, 3\rangle\}\) \[I_X=\{\langle 1, 1\rangle, \langle 2, 2\rangle, \langle 3, 3\rangle\},\,\,D_X=\{\langle 1, 1\rangle, \langle 1, 2\rangle, \langle 1, 3\rangle, \langle 2, 2\rangle, \langle 3, 3\rangle\}\] \[L_X=\{\langle 1, 1\rangle, \langle 1, 2\rangle, \langle 1, 3\rangle, \langle 2, 2\rangle, \langle 2, 3\rangle, \langle 3, 3\rangle\},\,\,L_{X^\prime}=\{\langle 1, 2\rangle, \langle 1, 3\rangle, \langle 2, 3\rangle\}\]

关系矩阵

定义: 设\(X, Y\)是两个有限集合, \(R\)是\(X\)到\(Y\)的二元关系, 并且 \(X=\{x_1, x_2, \cdots, x_m\}, Y=\{y_1, y_2, \cdots, y_n\}\), 则\(R\)的关系矩阵\(M_R\)(或\(M(R)\))是一个\(m\)行\(n\)列矩阵, 矩阵中元素\(m_{ij}\)的值定义为: \[ m_{ij}= \begin{cases} 0 &\langle x_i, y_j\rangle\notin R\\ 1 &\langle x_i, y_j\rangle\in R \end{cases}\,\,\,\,\,1\le i\le m, 1\le j\le n\]

例: 设\(A=\{x_1, x_2, x_3, x_4\}\), \(B=\{y_1, y_2, y_3\}\), \(A\)到\(B\)的二元关系: \(R=\{\langle x_1, y_1\rangle, \langle x_1, y_3\rangle, \langle x_2, y_2\rangle, \langle x_2, y_3\rangle, \langle x_3, y_1\rangle, \langle x_4, y_1\rangle, \langle x_4, y_2\rangle\}\). 求\(R\)的关系矩阵\(M_R\).

\[M_R=\left( \begin{matrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 0 & 0\\ 1 & 1 & 0 \end{matrix} \right) \]

例: 设\(A=\{x_1, x_1, x_3, x_4\}\), \(A\)上的二元关系: \[R=\{\langle x_1, x_1\rangle, \langle x_1, x_3\rangle, \langle x_2, x_3\rangle, \langle x_2, x_4\rangle, \langle x_3, x_1\rangle, \langle x_3, x_2\rangle, \langle x_4, x_4\rangle\}, \] 求\(R\)的关系矩阵\(M_R\).

\[M_R=\left( \begin{matrix} 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 1\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{matrix}\right) \]

关系图

设\(X=\{x_1, x_2, \cdots, x_m\}\), \(Y=\{y_1, y_2, \cdots, y_n\}\)是两个有限集, \(R\)是\(X\)到\(Y\)的二元关系.

\(R\)的关系图\(G_R\)或\(G(R)\)是一个有向图, 画法如下:

对于\(X\)中的每个元素\(x_i\), 在平面上画1个小圆圈来表示;对应\(Y\)中的每个元素\(y_j\), 在平面上画1个小圆圈来表示.每个元素对应的小圆圈称为结点.
若\(\langle x_i, y_j\rangle\in R\), 则画1条从结点\(x_i\)到结点\(y_j\)的有向线段.有向线段两端点中箭头指向的结点称为终点, 另1个端点称为始点.

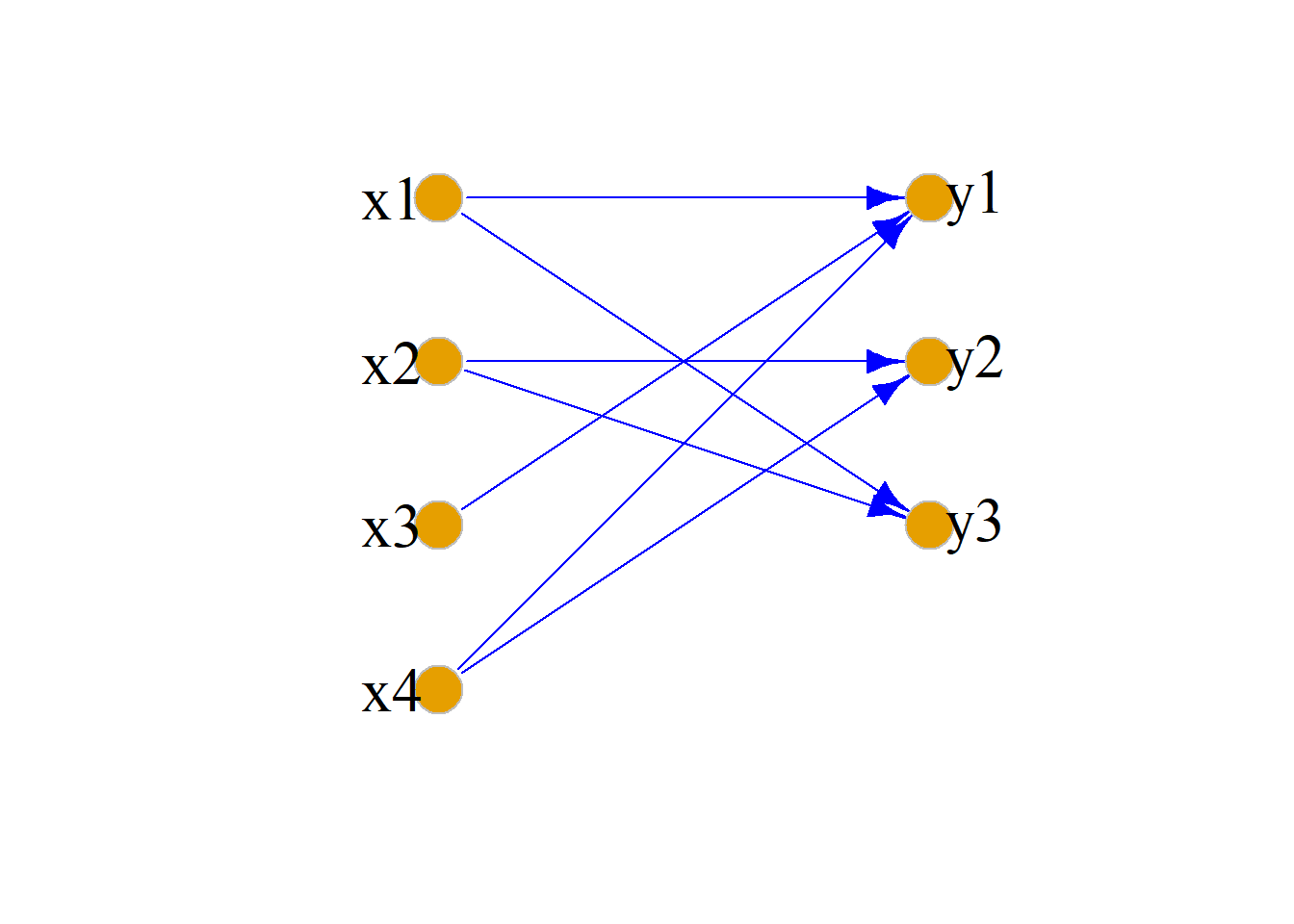
例: 设\(A=\{x_1, x_2, x_3, x_4\}\), \(B=\{y_1, y_2, y_3\}\),

\(A\)到\(B\)的二元关系: \[R=\{\langle x_1, y_1\rangle, \langle x_1, y_3\rangle, \langle x_2, y_2\rangle, \langle x_2, y_3\rangle, \] \[\langle x_3, y_1\rangle, \langle x_4, y_1\rangle, \langle x_4, y_2\rangle\}, \] 求\(R\)的关系图\(G_R\).

\[M_R=\left( \begin{matrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 0 & 0\\ 1 & 1 & 0 \end{matrix}\right) \]

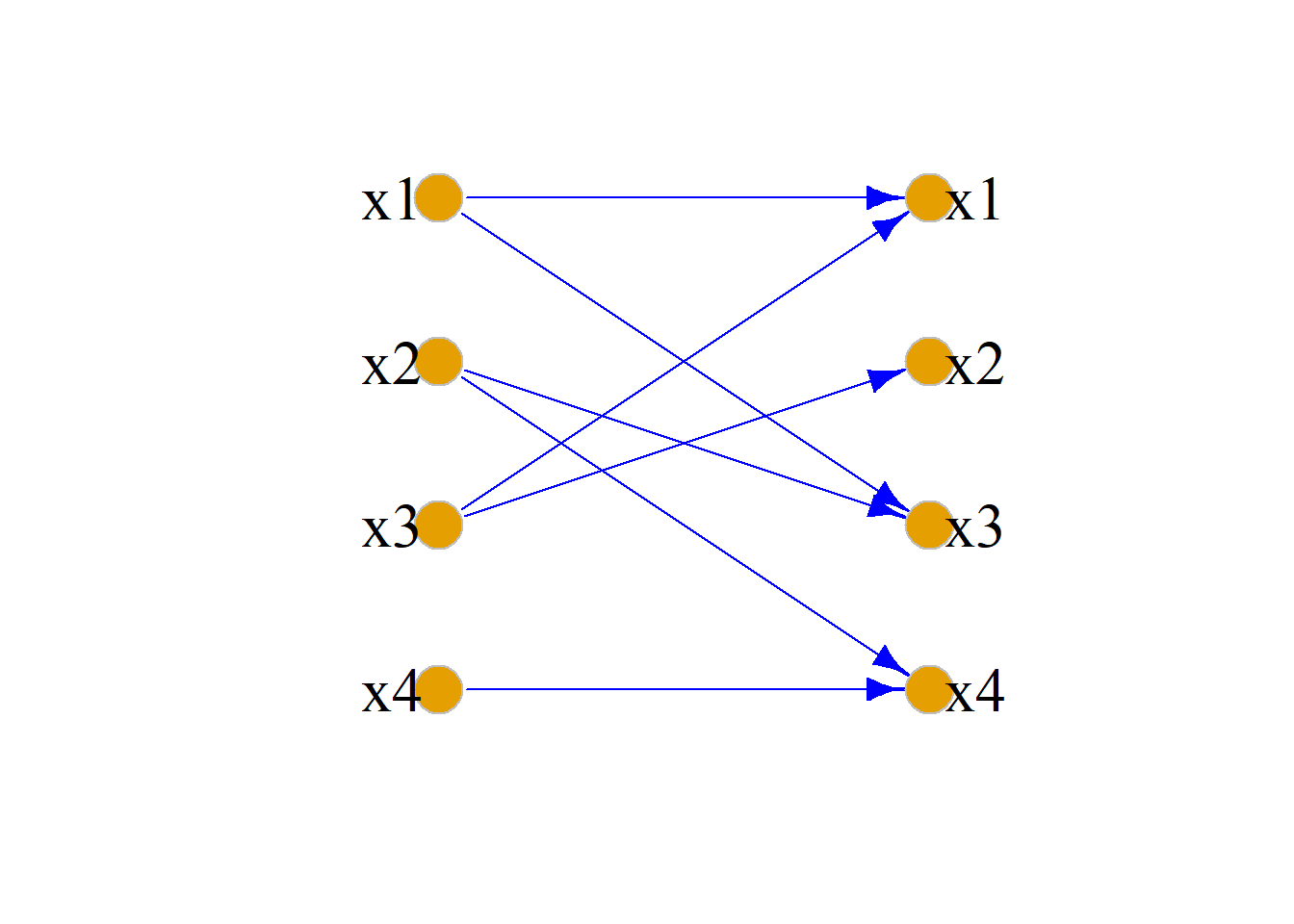
例: 设\(A=\{x_1, x_2, x_3, x_4\}\), \(A\)上的二元关系: \[R=\{\langle x_1, x_1\rangle, \langle x_1, x_3\rangle, \langle x_2, x_3\rangle, \langle x_2, x_4\rangle, \] \[\langle x_3, x_1\rangle, \langle x_3, x_2\rangle, \langle x_4, x_4\rangle\}, \] 求\(R\)的关系图\(G_R\).

\[M_R=\left( \begin{matrix} 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 1\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{matrix}\right) \]

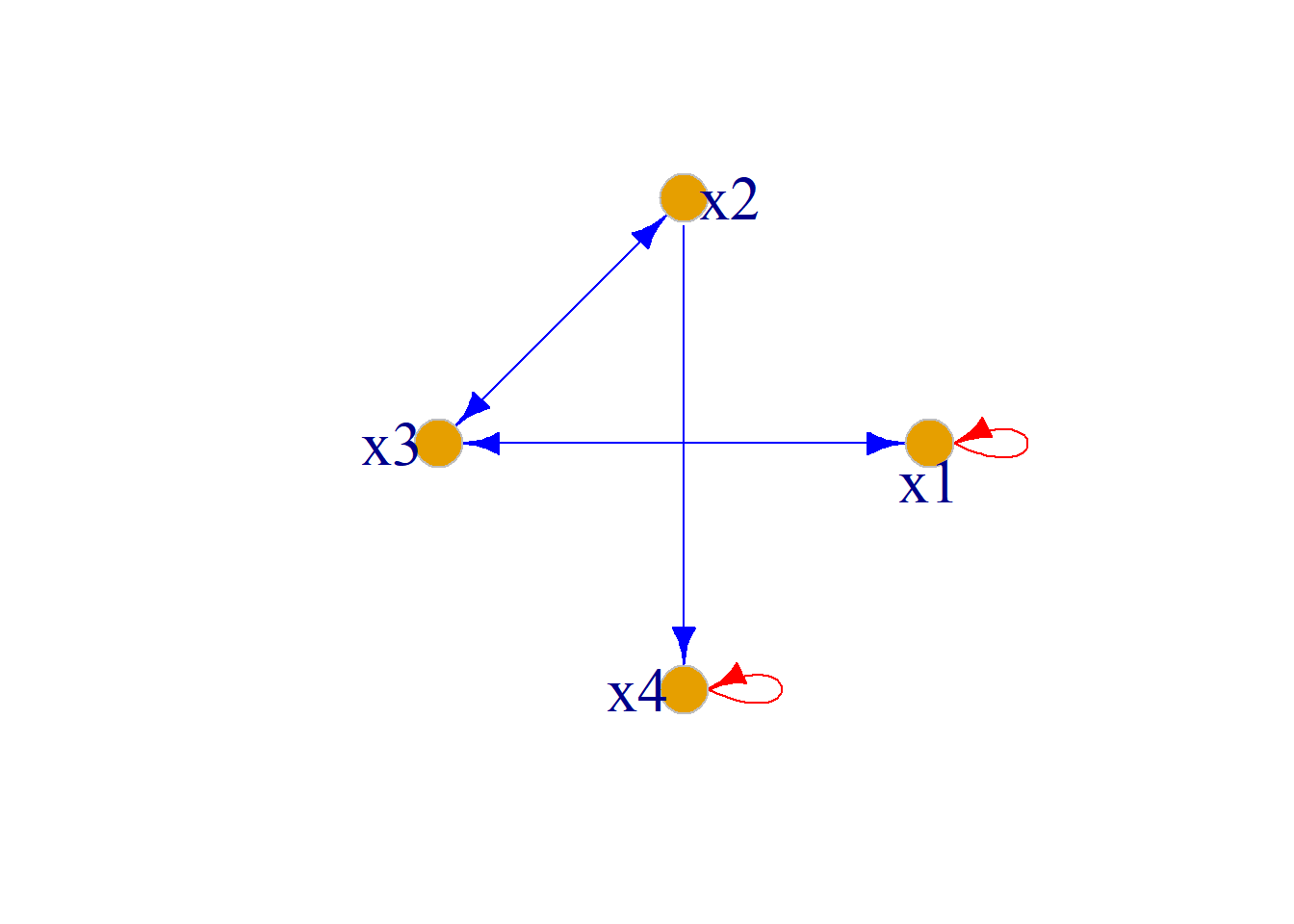
\[R=\{\langle x_1, x_1\rangle, \langle x_1, x_3\rangle, \langle x_2, x_3\rangle,\] \[\langle x_2, x_4\rangle, \langle x_3, x_1\rangle, \langle x_3, x_2\rangle, \langle x_4, x_4\rangle\}\]

由于\(A=B\), 因此关系图中也可以只画出\(A\)中的每个元素.

例: 设 \(X=\{1, 2, 3\}, Y=\{a, b, c\}\), \[R=\{\langle 1, a\rangle, \langle 1, b\rangle, \langle 2, b\rangle, \langle 2, c\rangle, \]

\[\langle 3, a\rangle, \langle 3, c\rangle \}\]

求\(R\)的关系矩阵和关系图.

解: \(R\)的关系矩阵为:

\[M_R=\left( \begin{matrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 1 & 0 & 1 \end{matrix}\right) \]

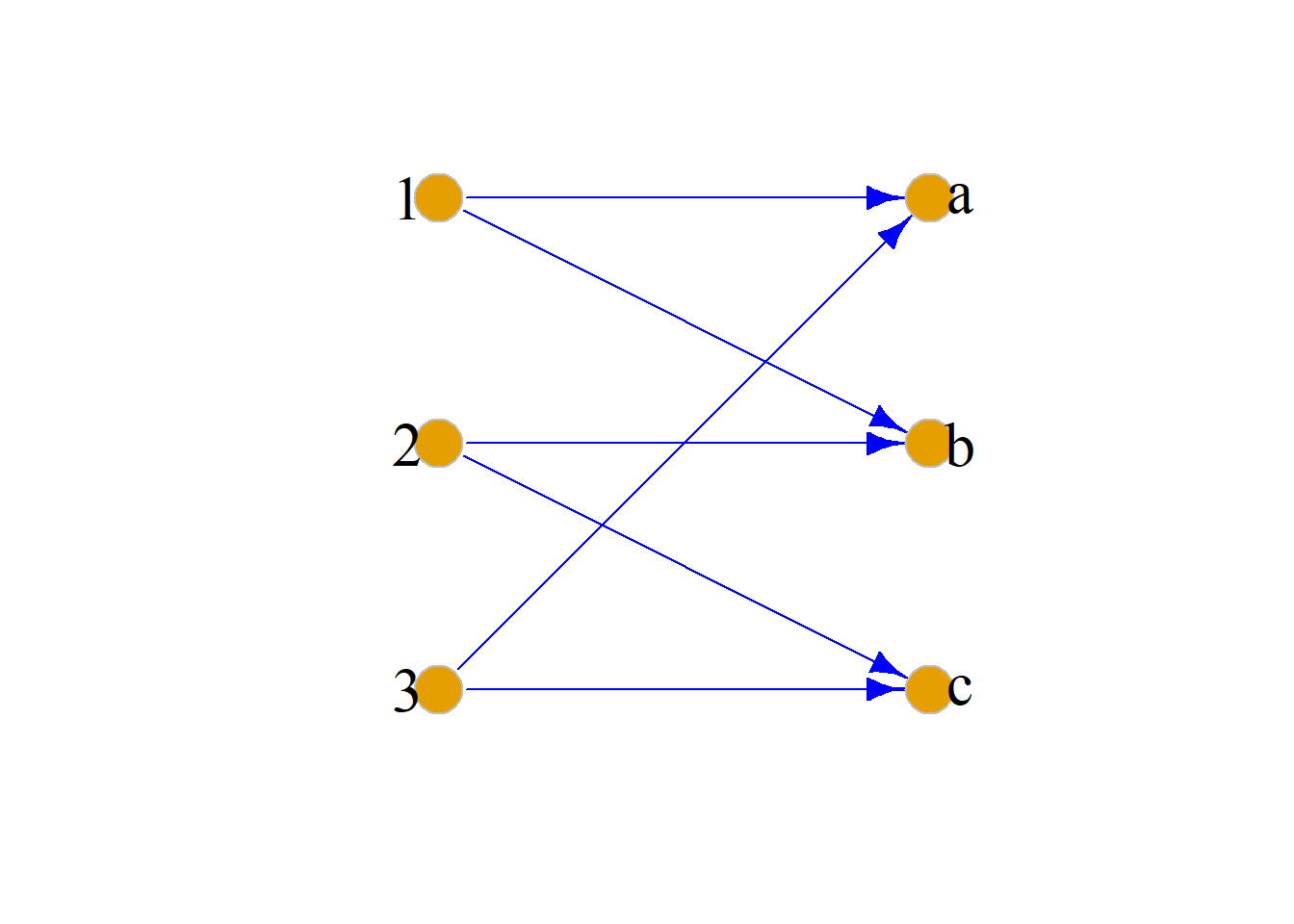
例: 设集合\(A=B=\{a, b, c\}\), 从\(A\)到\(B\)的二元关系是:

\[R=\{\langle a, b\rangle, \langle b, c\rangle, \langle a, c\rangle\}, \]

画出\(R\)的关系图.

关系的运算

逆关系(关系的逆运算)

定义: 设\(R\)是从集合\(X\)到集合\(Y\)的二元关系, \(R=\{\langle a, b\rangle |a\in X\wedge b\in Y\},\)

则

\(R^{-1}=\{\langle b, a\rangle |\langle a, b\rangle\in R\}\)

称为\(R\)的逆关系.

显然, \(R^{-1}\)为集合\(Y\)到\(X\)的二元关系.

例: 设集合\(X=\{1, 2, 3, 4\}, Y=\{a, b, c\}\), \(R\)是从\(X\)到\(Y\)的二元关系, 且 \(R=\{\langle 1, a\rangle, \langle 2, b\rangle, \langle 3, c\rangle, \langle 4, c\rangle\}\), 求\(R^{-1}\)

解: \[R^{-1}=\{\langle a, 1\rangle, \langle b, 2\rangle, \langle c, 3\rangle, \langle c, 4\rangle\}\]

定理: 设\(R\)和\(S\)都是从集合\(X\)到集合\(Y\)的二元关系, \(D(R)\)和\(V(R)\)分别表示\(R\)的定义域和值域, \(\sim R=(X\times Y)-R\), 则下列各式成立:

\(D(R^{-1})=V(R)\)
\(V(R^{-1})=D(R)\)
\((R^{-1})^{-1}=R\)
\((R\cup S)^{-1}=R^{-1}\cup S^{-1}\)

\((R\cap S)^{-1}=R^{-1}\cap S^{-1}\)
\((X\times Y)^{-1}=Y\times X\)
\((\Phi)^{-1}=\Phi\)
\(R=S\Leftrightarrow R^{-1}=S^{-1}\)
\(R\subseteq S\Leftrightarrow R^{-1}\subseteq S^{-1}\)
\((\sim R)^{-1}=\sim(R^{-1})\)
\((R-S)^{-1}=R^{-1}-S^{-1}\)

求证: \((R\cap S)^{-1}=R^{-1}\cap S^{-1}\)

证明: 对于任意的\(\langle y, x\rangle\),

若\(\langle y, x\rangle\in (R\cap S)^{-1}\), 则:

\[\langle x, y\rangle\in R\cap S\] \[\langle x, y\rangle\in R\wedge\langle x, y\rangle\in S\] \[\langle y, x\rangle\in R^{-1}\wedge\langle y, x\rangle\in S^{-1}\] \[\langle y, x\rangle\in R^{-1}\cap S^{-1}\] 所以\[(R\cap S)^{-1} \subseteq R^{-1}\cap S^{-1}.\]

对于任意的\(\langle y, x\rangle\), 若\(\langle y, x\rangle\in R^{-1}\cap S^{-1}\), 则:

\[\langle y, x\rangle\in R^{-1}\wedge\langle y, x\rangle\in S^{-1}\] \[\langle x, y\rangle\in R\wedge\langle x, y\rangle\in S\] \[\langle x, y\rangle\in R\cap S\] \[\langle y, x\rangle\in (R\cap S)^{-1}\]

所以 \[R^{-1}\cap S^{-1}\subseteq (R\cap S)^{-1}\]

故\[(R\cap S)^{-1}=R^{-1}\cap S^{-1}.\]

求证: \[(R-S)^{-1}=R^{-1}-S^{-1}.\]

证明:

\[(R-S)^{-1}=(R\cap \sim S)^{-1}\] \[=R^{-1}\cap (\sim S)^{-1}\] \[=R^{-1}\cap \sim (S^{-1})\] \[=R^{-1} – S^{-1}\]

所以\[(R-S)^{-1}=R^{-1}–S^{-1}.\]

设 \[A=\{x_1, x_2, \cdots , x_m\}, \] \[B=\{y_1, y_2, \cdots , y_n\}, \]

\(R\)是\(A\)到\(B\)的二元关系.

则\(R^{-1}\)是\(B\)到\(A\)的二元关系, 且它们的关系矩阵有如下关系:

\[ M_R= \left( \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) \] \[ M_{R^{-1}}= \left( \begin{array}{rrrr} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{array} \right) \] \[M_{R^{-1}}=(M_R)^T\]

设 \[A=\{x_1, x_2, \cdots , x_m\}, \] \[B=\{y_1, y_2, \cdots , y_n\}, \]

\(R\)是\(A\)到\(B\)的二元关系, 则\(R^{-1}\)是\(B\)到\(A\)的二元关系, 且它们的关系图有以下关系:

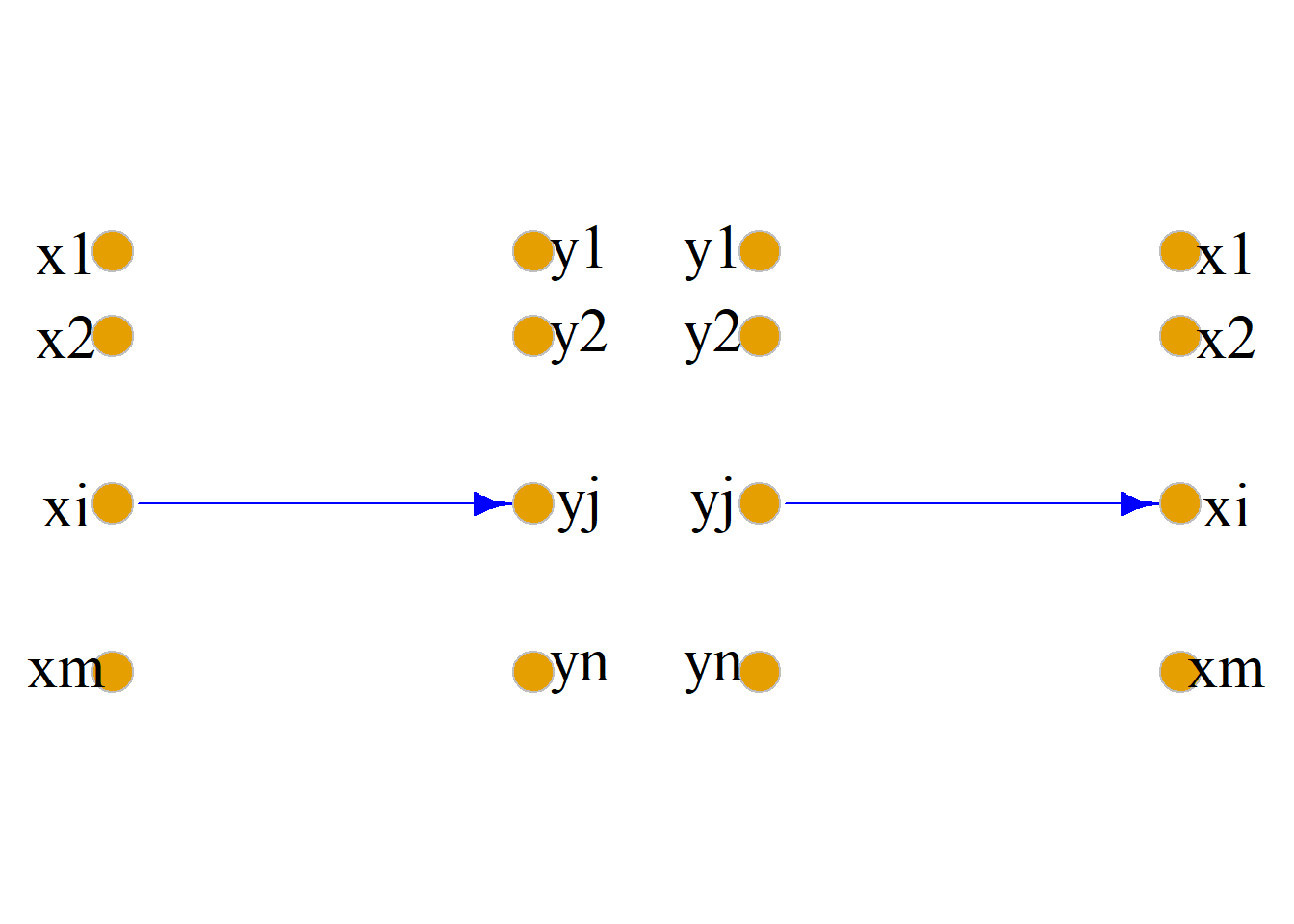
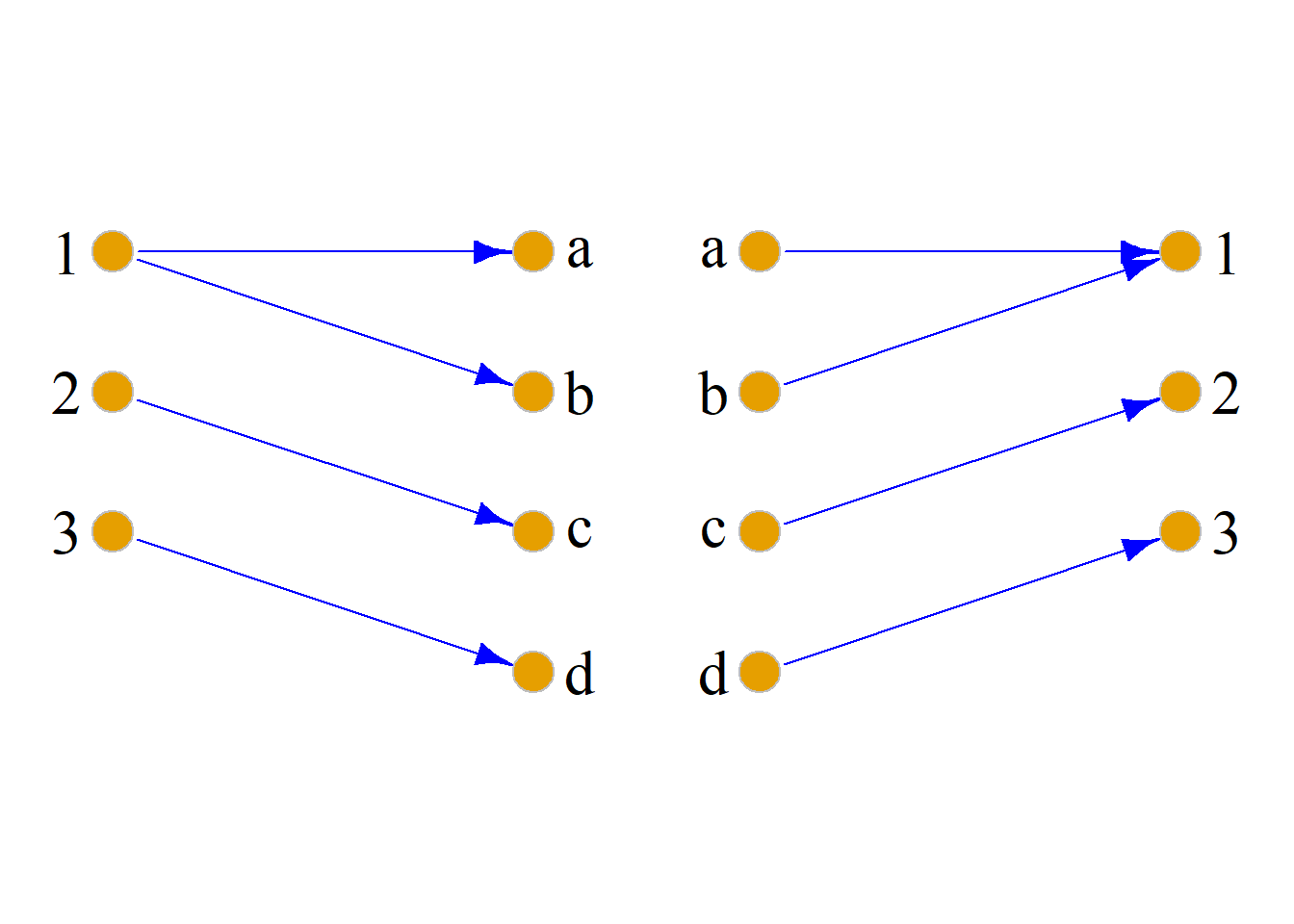
例: 设 \(X=\{1, 2, 3\}\), \(Y=\{a, b, c, d\}\), \[R=\{{\langle}1, a{\rangle}, {\langle}1, b{\rangle}, {\langle}2, c{\rangle}, {\langle}3, d{\rangle} \}\] 求\(R\)和\(R^{-1}\)的关系矩阵和关系图.

解: \(R^{-1} =\{{\langle}a, 1{\rangle}, {\langle}b, 1{\rangle}, {\langle}c, 2{\rangle}, {\langle}d, 3{\rangle}\}\),

所以\(R\)和\(R^{-1}\)的关系矩阵和关系图为:

\[ M_R= \left( \begin{array}{rrrr} 1&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{array} \right) \] \[ M_{R^{-1}}= \left( \begin{array}{rrr} 1&0&0\\ 1&0&0\\ 0&1&0\\ 0&0&1 \end{array} \right) \]

复合关系 (关系的复合运算)

定义: 设\(R\)是从集合\(X\)到集合\(Y\)的一个二元关系, \(S\)是从集合\(Y\)到集合\(Z\)的一个二元关系.

则\(R\)与\(S\)的复合关系(合成关系)\(R{\cdot}S\)是一个从\(X\)到\(Z\)的二元关系, 表示为: \[R{\cdot}S=\{{\langle}x, z{\rangle}|x{\in}X, z{\in}Z, \exists y{\in}Y, {\langle}x, y{\rangle}{\in}R∧{\langle}y, z{\rangle}{\in}S)\}\]

例: 设集合\(X=\{1, 2, 3\}\), \(Y=\{a, b, c\}\), \(Z=\{\alpha, \beta, \gamma\}\),

\(R\)是从\(X\)到\(Y\)的关系, \(S\)是从\(Y\)到\(Z\)的关系: \[R=\{{\langle}1, a{\rangle}, {\langle}2, b{\rangle}, {\langle}2, c{\rangle}\}\]

\[S=\{{\langle}a, \beta{\rangle}, {\langle}b, \alpha{\rangle}, {\langle}c, \gamma{\rangle}, {\langle}c, \beta{\rangle}\}\]

求\(R{\cdot}S\).

解: \[R{\cdot}S=\{{\langle}1, \beta{\rangle}, {\langle}2, \alpha{\rangle}, {\langle}2, \gamma{\rangle}, {\langle}2, \beta{\rangle}\}.\]

例: 设\(X=\{0, 1, 2, 3\}\), \(X\)上的二元关系: \[R=\{{\langle}i, j{\rangle}|j=i+1\, or\, i=2j\}, \] \[T=\{{\langle}i, j{\rangle}|i=j+2\}, \] 求\(R{\cdot}T\)和\(T{\cdot}R\).

解: \[R=\{{\langle}0, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}0, 0{\rangle}, {\langle}2, 1{\rangle}\}\] \[T=\{{\langle}2, 0{\rangle}, {\langle}3, 1{\rangle}\}\] \[R{\cdot}T=\{{\langle}1, 0{\rangle}, {\langle}2, 1{\rangle}\}\] \[T{\cdot}R=\{{\langle}2, 1{\rangle}, {\langle}2, 0{\rangle}, {\langle}3, 2{\rangle}\} \]

例: 设集合\(X=\{1, 2, 3, 4, 5\}\), \(R\), \(S\), \(T\)均是\(X\)上的二元关系:

\(R=\{{\langle}1, 2{\rangle}, {\langle}3, 4{\rangle}, {\langle}2, 2{\rangle}\},\,\,S=\{{\langle}4, 2{\rangle}, {\langle}2, 5{\rangle}, {\langle}3, 1{\rangle}, {\langle}1, 3{\rangle}\},\,\,T=\{{\langle}2, 3{\rangle}, {\langle}4, 1{\rangle}\}\)

求\(R{\cdot}S\), \(S{\cdot}R\), \((R{\cdot}S){\cdot}T\), \(R{\cdot}(S{\cdot}T)\)

解: \[R{\cdot}S=\{{\langle}1, 5{\rangle}, {\langle}3, 2{\rangle}, {\langle}2, 5{\rangle}\}\] \[S{\cdot}R=\{{\langle}4, 2{\rangle}, {\langle}3, 2{\rangle}, {\langle}1, 4{\rangle}\}\] \[(R{\cdot}S){\cdot}T =\{ {\langle}3, 3{\rangle} \}\] \[S{\cdot}T=\{ {\langle}4, 3{\rangle} \},\] \[R{\cdot}(S{\cdot}T)=\{ {\langle}3, 3{\rangle} \}\] \[R{\cdot}S {\neq} S{\cdot}R,\] \[(R{\cdot}S){\cdot}T =R{\cdot}(S{\cdot}T)\]

复合关系的关系图:

设:

\(A=\{x_1, x_2, \cdots , x_m\}\),

\(B=\{y_1, y_2, \cdots , y_n\}\),

\(C=\{z_1, z_2, \cdots , z_p\}\),

\(R\)是从集合\(A\)到集合\(B\)的二元关系,

\(S\)是从集合\(B\)到集合\(C\)的二元关系,

则复合关系\(R\cdot S\)的关系图画法如下:

对应\(A\)中的每一个元素\(x_i\)(\(i=1, 2, \cdots , m\)), 在平面上画一个结点. 同样对应\(C\)中的每一个元素\(z_k\)(\(k=1, 2, \cdots , p\)), 在平面上画一个结点. 得关系图\(G_{R{\cdot}S}\)的所有结点.

在\(G_{R{\cdot}S}\)中画出所有满足下面条件的有向边:若在\(G_{R}\)中有\(x_i\)到\(y_j\)的有向边, 且在\(G_{S}\)中有\(y_j\)到\(z_k\)的有向边, 则在\(G_{R{\cdot}S}\)中画一条从\(x_i\)到\(z_k\)的有向边.

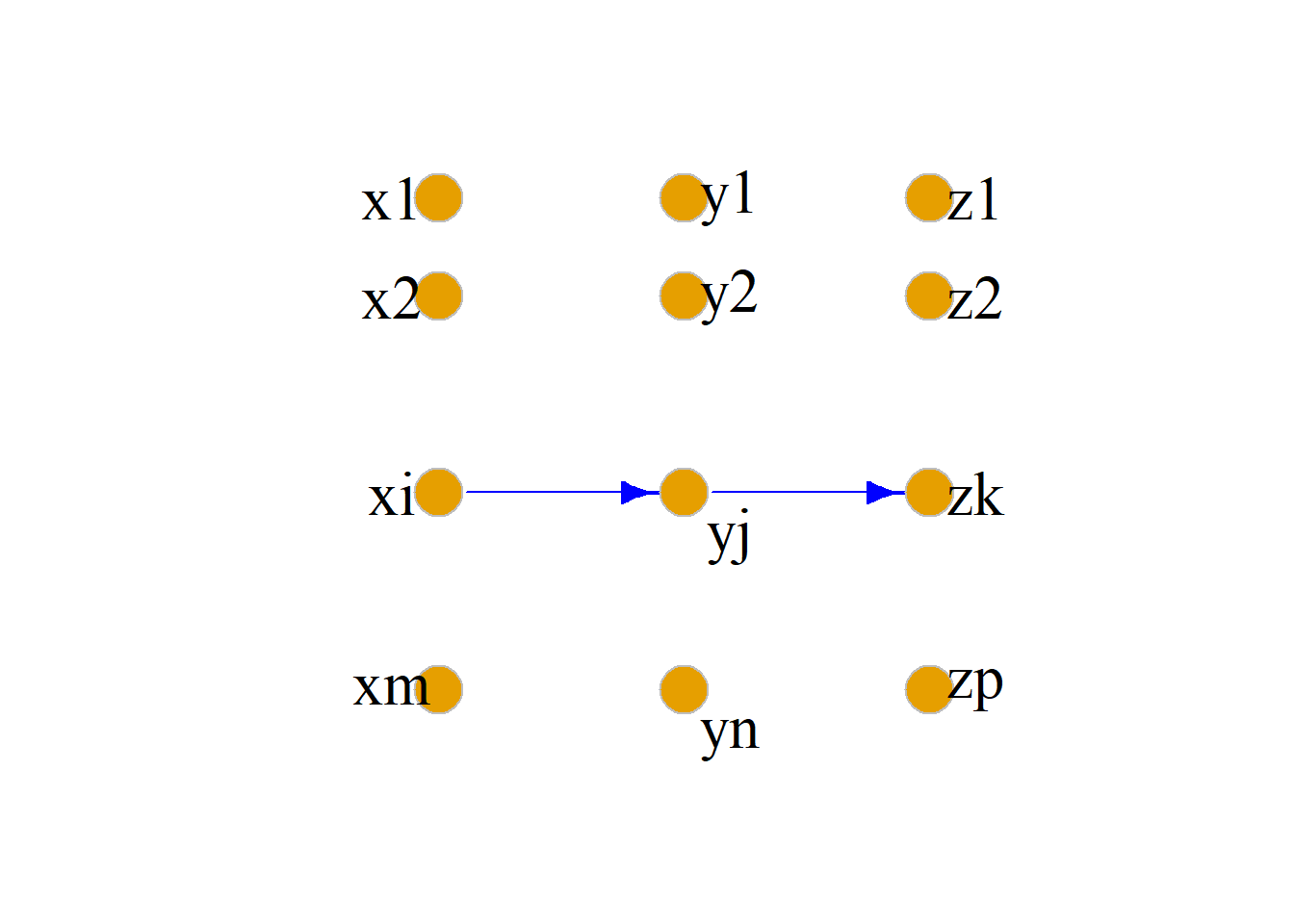
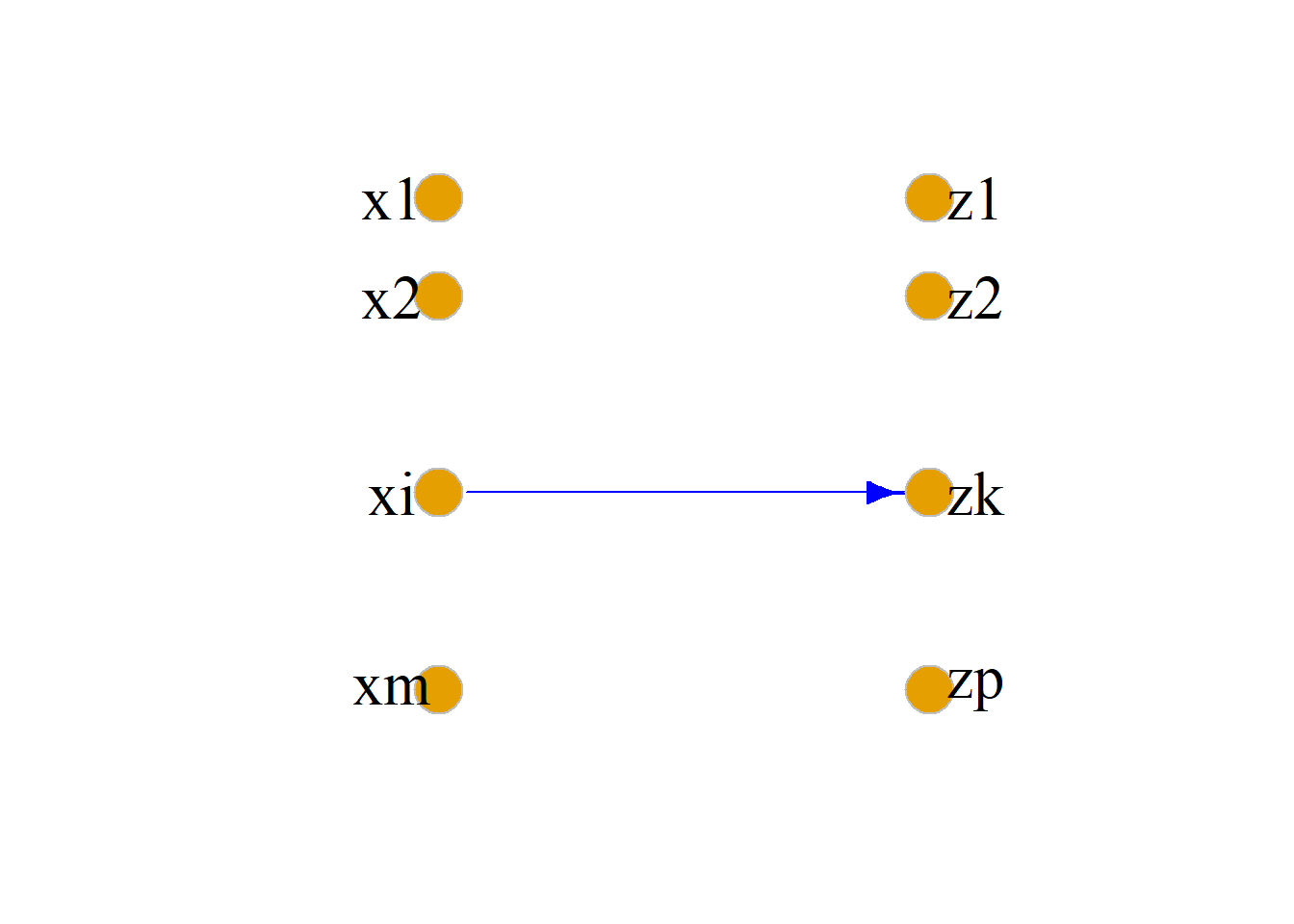
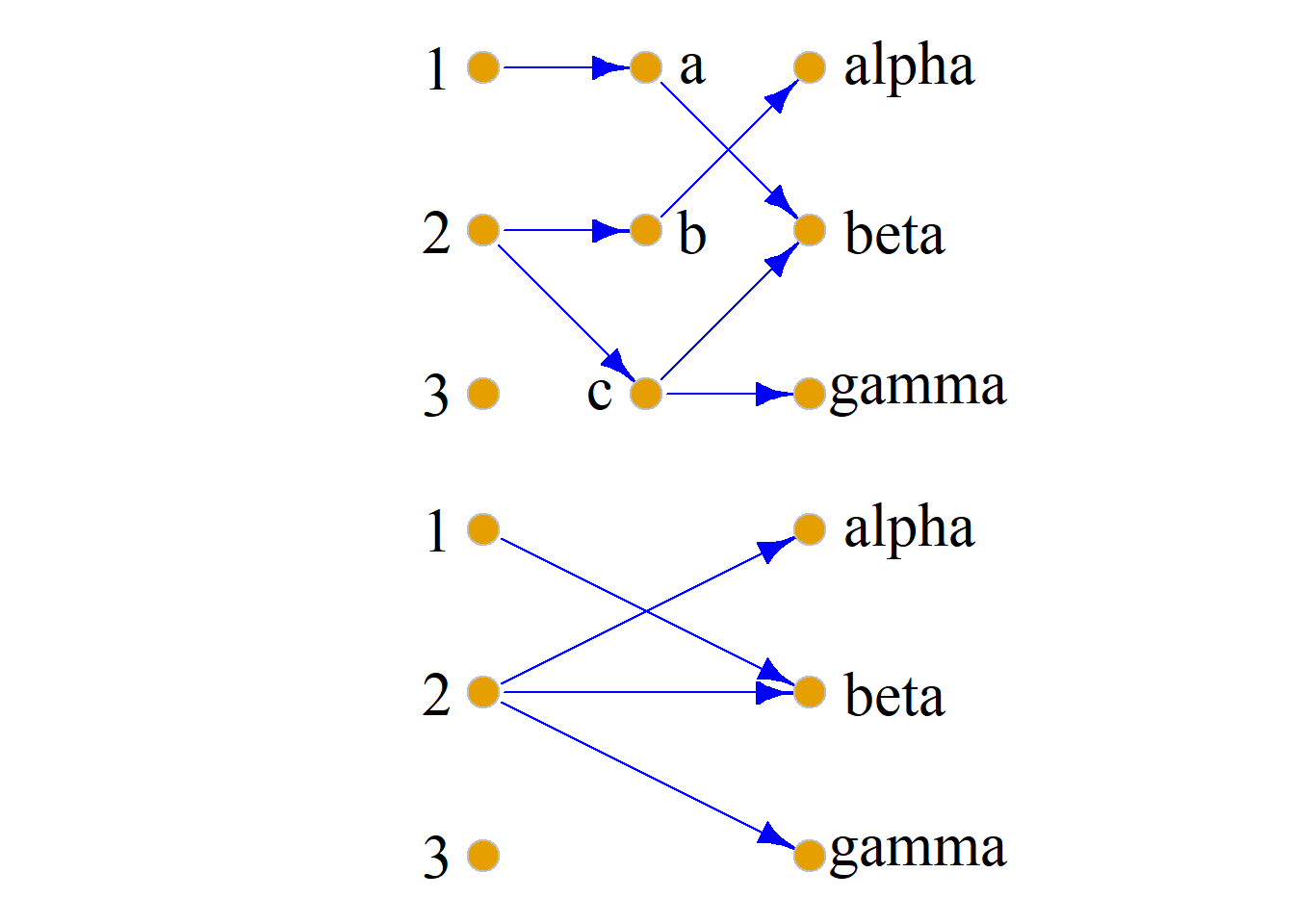
例: 设集合\(X=\{1, 2, 3\}\), \(Y=\{a, b, c\}\), \(Z=\{\alpha, \beta, \gamma\}\),

\(R\)是从\(X\)到\(Y\)的关系. \(S\)是从\(Y\)到\(Z\)的关系. \[R=\{{\langle}1, a{\rangle}, {\langle}2, b{\rangle}, {\langle}2, c{\rangle}\}\] \[S=\{{\langle}a, \beta{\rangle}, {\langle}b, \alpha{\rangle}, {\langle}c, \beta{\rangle}\}, {\langle}c, \gamma{\rangle}\] 求\(G_{R{\cdot}S}\)

解: \[R{\cdot}S =\{{\langle}1, \beta{\rangle}, {\langle}2, \alpha{\rangle}, {\langle}2, \beta{\rangle}, {\langle}2, \gamma{\rangle}\}\] \(R{\cdot}S\)复合关系\(R{\cdot}S\)的关系图:

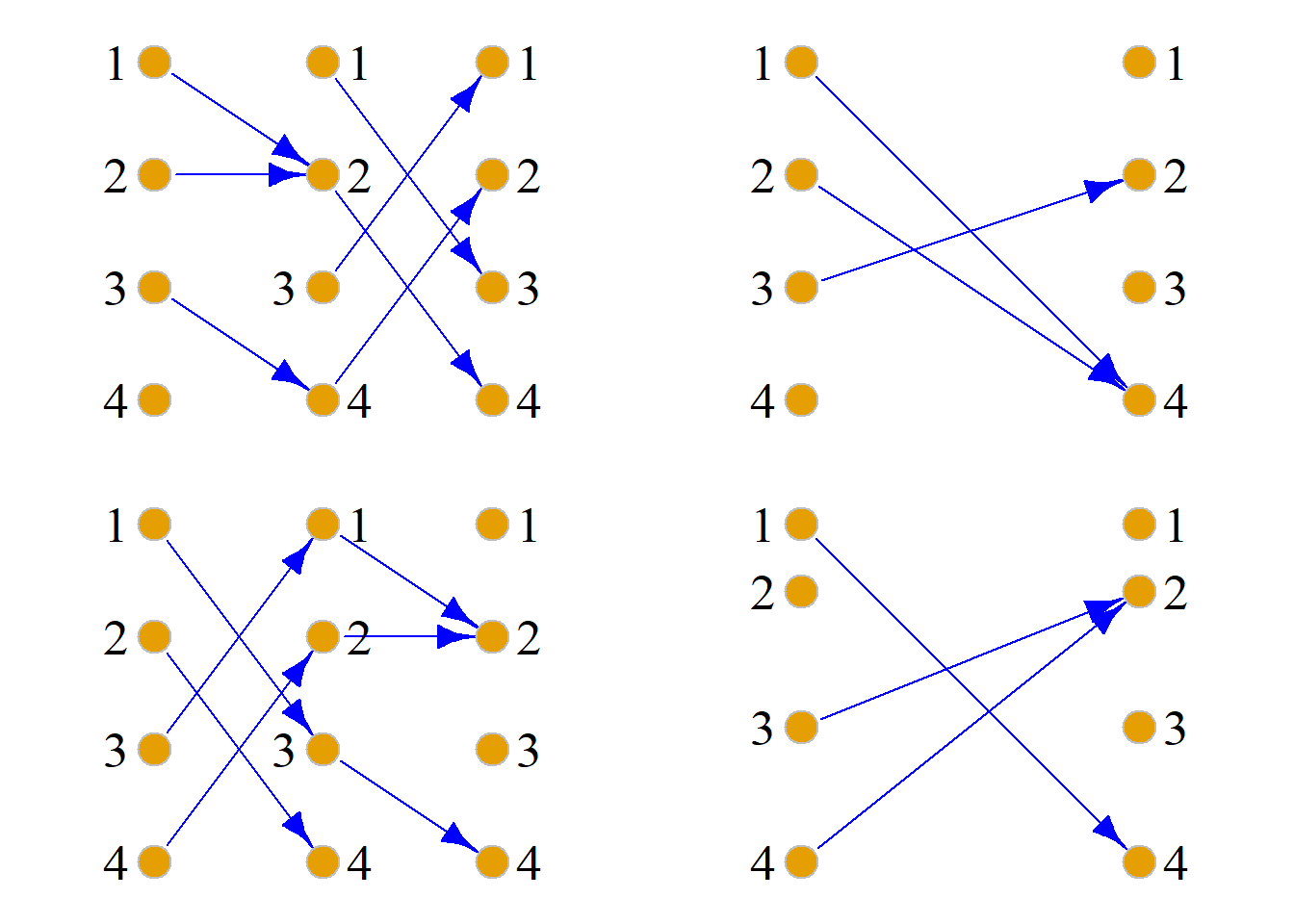
例: 设集合\(X=\{1, 2, 3, 4\}\), \(R\), \(T\)均是\(X\)上的二元关系: \[R=\{{\langle}1, 2{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 4{\rangle}\}\] \[T=\{{\langle}1, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 1{\rangle}, {\langle}4, 2{\rangle}\}\]

求\(G_{R{\cdot}T}\)和\(G_{T{\cdot}R}\).

\[R{\cdot}T =\{{\langle}1, 4{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}\}\]

\[T{\cdot}R =\{{\langle}1, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}4, 2{\rangle}\}\]

\[T\cdot R \neq R\cdot T\]

复合关系的关系矩阵也可以通过矩阵的逻辑乘法来求得.

定理: 复合关系的关系矩阵等于各关系矩阵的逻辑乘.

设: \(A=\{x_1, x_2, \cdots , x_m\}\), \(B=\{y_1, y_2, \cdots , y_n\}\), \(C=\{z_1, z_2, \cdots , z_p\}\),

\(R\)是\(A\)到\(B\)的二元关系, \(S\)是\(B\)到\(C\)的二元关系, 则

\(M_{R{\cdot}S}= M_R{\times}M_S\)

\[ \left( \begin{array}{rrr} 0&1&1\\ 0&0&1\\ 1&0&1 \end{array} \right) \left( \begin{array}{rrr} 0&1&1\\ 1&0&1\\ 0&0&1 \end{array} \right) = \left( \begin{array}{rrr} 1&0&1\\ 0&0&1\\ 0&1&1 \end{array} \right) \]

设:\(A\)是\(m{\times}n\)矩阵:

\[\qquad\qquad A= \left( \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) \] \(B\)是\(n{\times}p\)矩阵:

\[\qquad\qquad B= \left( \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1p} \\ a_{21} & a_{22} & \cdots & a_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{np} \end{array} \right) \]

则矩阵的逻辑乘运算\(C=A{\times}B\)定义为:

\[ C=A\times B= \left( \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1p} \\ a_{21} & a_{22} & \cdots & a_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mp} \end{array} \right) \] 这里, \[ c_{ik}=\vee_{j=1}^n(a_{ij}\wedge b_{jk}) \] \(a_{ij}\)、\(b_{jk}\)都只取0或1, 运算是逻辑运算.

例: 设有集合\(X=\{1, 2, 3, 4, 5\}\), \(X\)上的关系 \[R=\{{\langle}1, 2{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 4{\rangle}\}, \] \[T=\{{\langle}1, 3{\rangle}, {\langle}2, 5{\rangle}, {\langle}3, 1{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 2{\rangle}\}, \] 求\(M_{R{\cdot}T}\)和\(M_{T{\cdot}R}\)

\[ M_R=\left( \begin{array}{rrrrr} 0&1&0&0&0\\ 0&1&0&0&0\\ 0&0&0&1&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array} \right) \,\,\, M_T=\left( \begin{array}{rrrrr} 0&0&1&0&0\\ 0&0&0&0&1\\ 1&0&0&1&0\\ 0&1&0&0&0\\ 0&0&0&0&0 \end{array} \right) \]

\[ M_{R\cdot T}=\left( \begin{array}{rrrrr} 0&0&0&0&1\\ 0&0&0&0&1\\ 0&1&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array} \right) \] \[ M_{T\cdot R}=\left( \begin{array}{rrrrr} 0&0&0&1&0\\ 0&0&0&0&0\\ 0&1&0&0&0\\ 0&1&0&0&0\\ 0&0&0&0&0 \end{array} \right) \]

由\(M_{R{\cdot}T}\)和\(M_{T{\cdot}R}\)得到

\[R{\cdot}T=\{{\langle}1, 5{\rangle}, {\langle}2, 5{\rangle}, {\langle}3, 2{\rangle}\}\]

\[T{\cdot}R=\{{\langle}1, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}4, 2{\rangle}\}\]

复合运算的性质

满足结合律:

\[(R{\cdot}S){\cdot}P=R{\cdot}(S{\cdot}P)\]

不满足交换律:

\[R{\cdot}S\neq S{\cdot}R\]

复合运算对并运算满足分配律:

\[R{\cdot}(S{\cup}P)=(R{\cdot}S){\cup}(R{\cdot}P),\,\,(S{\cup}P){\cdot}R =(S{\cdot}R){\cup}(P{\cdot}R)\]

复合运算对交运算满足下面的包含关系

\[R{\cdot}(S{\cap}P)\subseteq(R{\cdot}S){\cap}(R{\cdot}P),\,\,(S{\cap}P){\cdot}R\subseteq(S{\cdot}R){\cap}(P{\cdot}R)\]

设\(R\)是\(X\)到\(Y\)的关系, \(I_x\)为\(X\)上的恒等关系, \(I_y\)为\(Y\)上的恒等关系, 则

\[I_x{\cdot}R=R{\cdot}I_y=R.\]

证明结合律: \((R{\cdot}S){\cdot}P=R{\cdot}(S{\cdot}P)\)

证明: 对任意的\({\langle}x, w{\rangle}{\in}(R{\cdot}S){\cdot}P\)，必存在 \(z{\in}Z\), 使得 \({\langle}x, z{\rangle}{\in}R{\cdot}S\) 且 \({\langle}z, w{\rangle}{\in}P\)

又必存在 \(y{\in}Y\), 使得 \({\langle}x, y{\rangle}{\in}R\) 及 \({\langle}y, z{\rangle}{\in}S\)

由于\({\langle}y, z{\rangle}{\in}S, {\langle}z, w{\rangle}{\in}P\), 故\({\langle}y, w{\rangle}{\in}S{\cdot}P.\)

由于\({\langle}x, y{\rangle}{\in}R\), \({\langle}y, w{\rangle}{\in}S{\cdot}P\), 故\({\langle}x, w{\rangle}{\in}R{\cdot}(S{\cdot}P)\).

故\(R{\cdot}(S{\cdot}P) \subseteq (R{\cdot}S){\cdot}P\).

同理可证: \(R{\cdot}(S{\cdot}P) \subseteq (R{\cdot}S){\cdot}P\)

因而\((R{\cdot}S){\cdot}P = R{\cdot}(S{\cdot}P).\)

定理: 设\(R\)是\(X\)到\(Y\)的二元关系, \(S\)是\(Y\)到\(Z\)的二元关系, 则\[(R{\cdot}S)^{-1}=S^{-1}{\cdot}R^{-1}\]

证明: 对任意的\({\langle}z, x{\rangle}\), 若\({\langle}z, x{\rangle}{\in}(R{\cdot}S)^{-1}\),

则\({\langle}x, z{\rangle}{\in}(R{\cdot}S)\),

故存在\(y{\in}Y\), 使\[{\langle}x, y{\rangle}{\in}R{\wedge}{\langle}y, z{\rangle}{\in}S\] 必有:

\[{\langle}y, x{\rangle}{\in}R^{-1} {\wedge} {\langle}z, y{\rangle}{\in}S^{-1}.\]

则\({\langle}z, y{\rangle}{\in}S^{-1}{\wedge}{\langle}y, x{\rangle}{\in}R^{-1}\)

故得: \({\langle}z, x{\rangle}{\in}S^{-1}{\cdot}R^{-1}\)

所以\((R{\cdot}S)^{-1} \subseteq S^{-1}{\cdot}R^{-1}\)

同理: \(S^{-1}{\cdot}R^{-1} \subseteq (R{\cdot}S)^{-1}\)

从而\((R{\cdot}S)^{-1}=S^{-1}{\cdot}R^{-1}.\)

幂运算

定义: 设\(R\)是集合\(A\)上的二元关系, \(n\)为自然数, \(R\)的\(n\)次幂记作\(R^n\), 并且规定

\(R^0=I_A, \,\,R^{n+1}= R^n{\cdot}R\)

由定义可以看出, 对于集合\(A\)上任意一个关系\(R\), 都有\(R^0=I_A\), \(R^1=R\).

例: 设\(X=\{1, 2, 3\}\), \(X\)中的二元关系\(R=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\) 求\(R\)的各次幂.

解: \[R^0=I_x=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\] \[R^1=R=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\] \[R^2=R{\cdot}R=\{{\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\] \[R^3=R^2{\cdot}R=\{{\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}{\cdot}\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle} \} =\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\} =R\]

\[R^4=R^3{\cdot}R=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}{\cdot}\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle} \}=\{{\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\} =R^2\]

\[R = R^3 =\cdots = R^{2n+1} = \{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\] \[R^2 = R^4 =\cdots = R^{2n+2} = \{{\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

例: 设\(A=\{a, b, c, d\}\), \(A\)上的二元关系: \(R=\{{\langle}a, b{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}, {\langle}c, d{\rangle}\}\), 求:\(R\)的各次幂.

解: \[R^0=I_A=\{{\langle}a, a{\rangle}, {\langle}b, b{\rangle}, {\langle}c, c{\rangle}, {\langle}d, d{\rangle}\}\] \[R^1=R =\{{\langle}a, b{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}, {\langle}c, d{\rangle}\}\] \[R^2=R{\cdot}R =\{{\langle}a, a{\rangle}, {\langle}a, c{\rangle}, {\langle}b, b{\rangle}, {\langle}b, d{\rangle}\}\] \[R^3=R^2{\cdot}R =\{{\langle}a, b{\rangle}, {\langle}a, d{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}\}\]

\[R^4=R^3{\cdot}R =\{{\langle}a, a{\rangle}, {\langle}a, c{\rangle}, {\langle}b, b{\rangle}, {\langle}b, d{\rangle}\} =R^2\]

\[R^5=R^4{\cdot}R =\{{\langle}a, b{\rangle}, {\langle}a, d{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}\} =R^3\]

\[ R^2 = R^{2n+2} = \{{\langle}a, b{\rangle}, {\langle}a, d{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}\} \]

\[R^3 = R^{2n+1}= \{{\langle}a, b{\rangle}, {\langle}a, d{\rangle}, {\langle}b, a{\rangle}, {\langle}b, c{\rangle}\}\]

设\(R\)是集合\(X\)中的二元关系, \(m, n{\in}N\), 则: \(R^m{\cdot}R^n = R^{m+n},\,\,(R^m)^n = R^{m\times n}.\)

关系的性质

定义: 设\(R\)是集合\(X\)中的二元关系, 若对于任意的\(x{\in}X\), 都有\({\langle}x, x{\rangle}{\in}R\), 则称\(R\)是自反关系(自反的).

例: 集合间的包含”\({\subseteq}\)“关系、数之间的小于等于”\({\leq}\)“关系、直线间的”平行”关系等都是自反关系.

定义: 设\(R\)是集合\(X\)中的二元关系, 若对于任意的\(x{\in}X\), 都有\({\langle}x, x{\rangle}{\notin}R\), 则称\(R\)是反自反关系(反自反的) .

例: 集合间的真包含”\({\subset}\)“关系; 数之间的小于”\(<\)“关系.

例: 设 \(X=\{1, 2, 3\}\), 判断以下\(X\)上的二元关系是否是自反关系或反自反关系: \(E_x, I_x, D_x, L_x, L_ {x^\prime}, R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}.\)

解: \[E_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, \] \[{\langle}2, 3{\rangle}, {\langle}3, 1{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

\[I_x=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

\[D_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

\[L_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\]

\[L_{X^\prime}=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

\[R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

自反关系、反自反关系在关系图上的反映:

如果\(R\)是自反的, 则其关系图中每个结点有环;
如果\(R\)是反自反的, 则其关系图中每个结点无环;
如果\(R\)是即非自反又非反自反的, 则其关系图中有些结点有环同时有些结点无环.

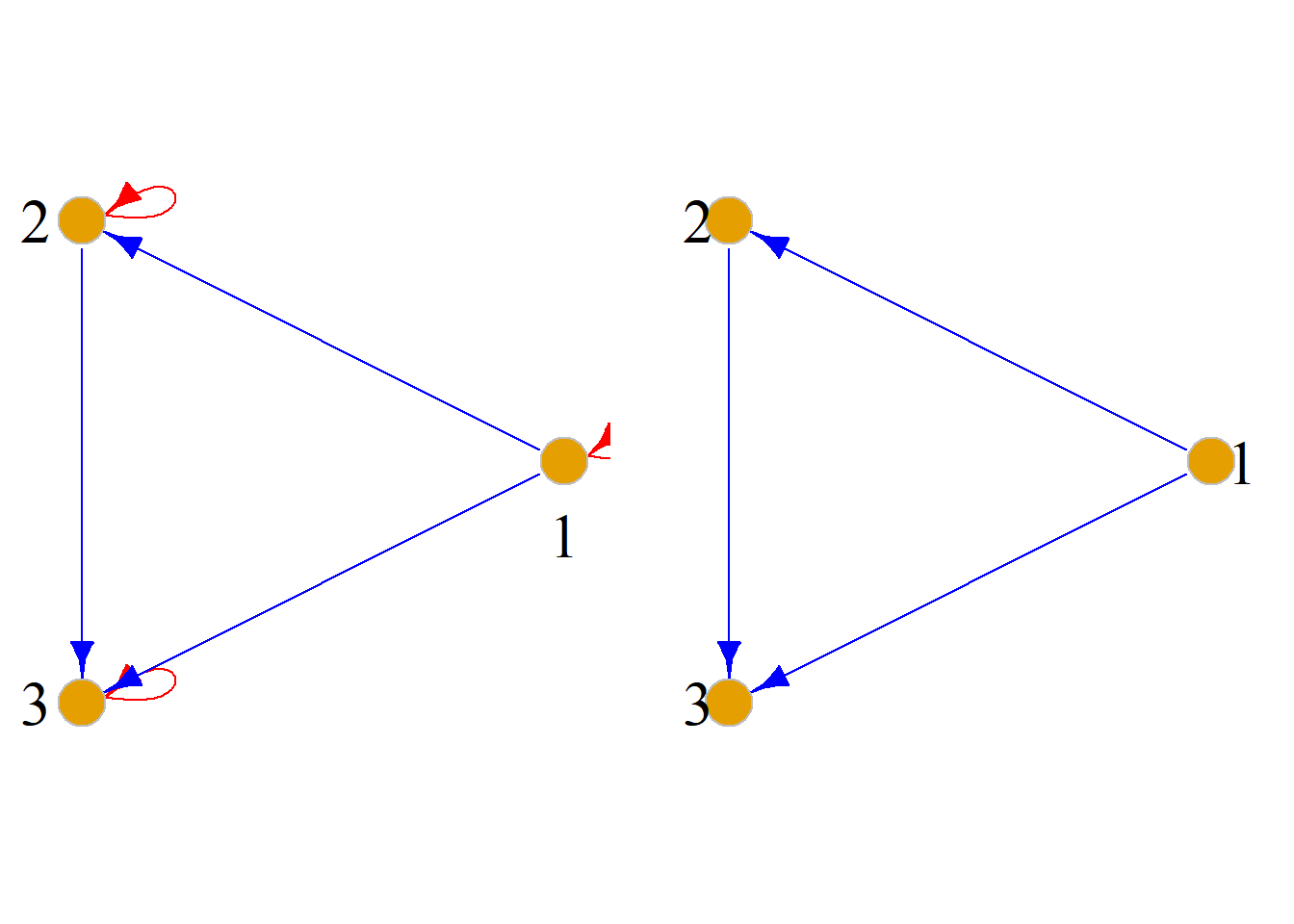
例: 设\(X=\{1, 2, 3\}\), \(X\)上二元关系如下, 画出关系图.

\[L_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\]

\[L_X^\prime=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

\[R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

自反关系、反自反关系在关系矩阵上的反映:

如果\(R\)是自反的, 则其关系矩阵的主对角线元素全为1;
如果\(R\)是反自反的, 则其关系矩阵的主对角线元素全为0;
如果\(R\)是即非自反又非反自反的, 则其关系矩阵的主对角线元素0和1同时存在.

例: 设\(X=\{1, 2, 3\}\), \(X\)上二元关系如下, 求关系矩阵.

\[L_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\},\,\,L_X^\prime=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

\[R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\] \[ L_x= \left( \begin{array}{ccc} 1&1&1\\ 0&1&1\\ 0&0&1 \end{array} \right) , \,\, L_{x^\prime}= \left( \begin{array}{ccc} 0&1&1\\ 0&0&1\\ 0&0&0 \end{array} \right) ,\,\, R= \left( \begin{array}{ccc} 1&0&1\\ 0&0&1\\ 0&0&0 \end{array} \right) \]

定理: 设\(R\)是集合\(A\)中的二元关系, 则:

\(R\)是自反的当且仅当\(I_A{\subset}R\)
\(R\)是反自反的当且仅当\(R{\cap}I_A={\Phi}\)

定理: 设\(R_1\)和\(R_2\)是集合\(A\)中的二元关系, 若\(R_1\), \(R_2\)是自反的, 则:

\(R_1^{-1}\)、\(R_1{\cup}R_2\)、\(R_1{\cap}R_2\)也是自反的.

证明: 设\(R_1\)是集合\(A\)中的自反关系. 任意取\(x{\in}A\), 有\({\langle}x, x{\rangle}{\in}R_1\), 则\({\langle}x, x{\rangle}{\in} R_1^{-1}\). 故\(R_1^{-1}\)也是自反的.

设\(R_1\) 和\(R_2\)是集合\(A\)中的自反关系. 任意取\(x{\in}A\), 有\({\langle}x, x{\rangle}{\in}R_1, {\langle}x, x{\rangle}{\in}R_2\), 则 \({\langle}x, x{\rangle}{\in}R_1{\cup}R_2\), 故\(R_1{\cup}R_2\)也是自反的.

设\(R_1\) 和\(R_2\)是集合\(A\)中的自反关系. 任意取\(x{\in}A\), 有\({\langle}x, x{\rangle}{\in}R_1, {\langle}x, x{\rangle}{\in}R_2\), 则 \({\langle}x, x{\rangle}{\in}R_1{\cap}R_2\), 故\(R_1{\cap}R_2\)也是自反的.

定义: 设\(R\)是集合\(X\)中的二元关系, 若对任意的\(x, y{\in}X\), 只要有\({\langle}x, y{\rangle}{\in}R\), 就必有\({\langle}y, x{\rangle}{\in}R\), 则称\(R\)是对称关系.

例: 数之间的相等“=”关系、两个三角形的“相似”关系.

定义: 设\(R\)是集合\(X\)中的二元关系, 若对任意的\(x, y{\in}X\), 当\({\langle}x, y{\rangle}{\in}R\)且\({\langle}y, x{\rangle}{\in}R\)时, 必有\(x=y\), 则称\(R\)是反对称关系.

例: 集合间的包含“\({\subseteq}\)”关系、数之间的小于等于”\({\leq}\)“关系.

例: 设 \(X=\{1, 2, 3\}\), \(R=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\), 判断\(R\)及以下\(X\)上的二元关系是否是对称关系或反对称关系: \(E_x, I_x, D_x, L_x, L_{x^\prime}, {\Phi}\).

\[D_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

\[L_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\]

\[L_X^\prime=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\} \]

\[ {\Phi} =\{\}\]

\[R =\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\] \(R\)既非对称关系, 也非反对称关系.

例: 设\(X=\{1, 2, 3\}\), 给出几个\(X\)上的对称关系和反对称关系.

解: \[R_1=\{{\langle}1, 1{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\},\,\, R_2=\{{\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}3, 1{\rangle}\}\] 等都是\(X\)上的对称关系. \[R_3=\{{\langle}1, 1{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 2{\rangle}\},\,\,R_4=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\},\,\,R_5=\{{\langle}3, 2{\rangle}\}\] 等都是反对称关系.

\[R_6=\{{\langle}3, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\] 这个关系既非对称又非反对称的. 而 \[R_7=\{{\langle}2, 2{\rangle}\}\] 既是对称的, 又是反对称的.

对称关系、反对称关系在关系图上的反映:

如果\(R\)是对称的, 则其关系图中, 若\(x_i\)到\(x_j\)有有向边, 则\(x_j\)到\(x_i\)也有有向边;
如果\(R\)是反对称的, 则其关系图中, 若\(x_i\)到\(x_j\)有有向边, 则\(x_j\)到\(x_i\)无有向边;
如果\(R\)是即非对称又非反对称的, 则其关系图中, 有些结点对之间有一对方向相反的边, 有些结点对之间只有一条边, 且两种情况同时存在.

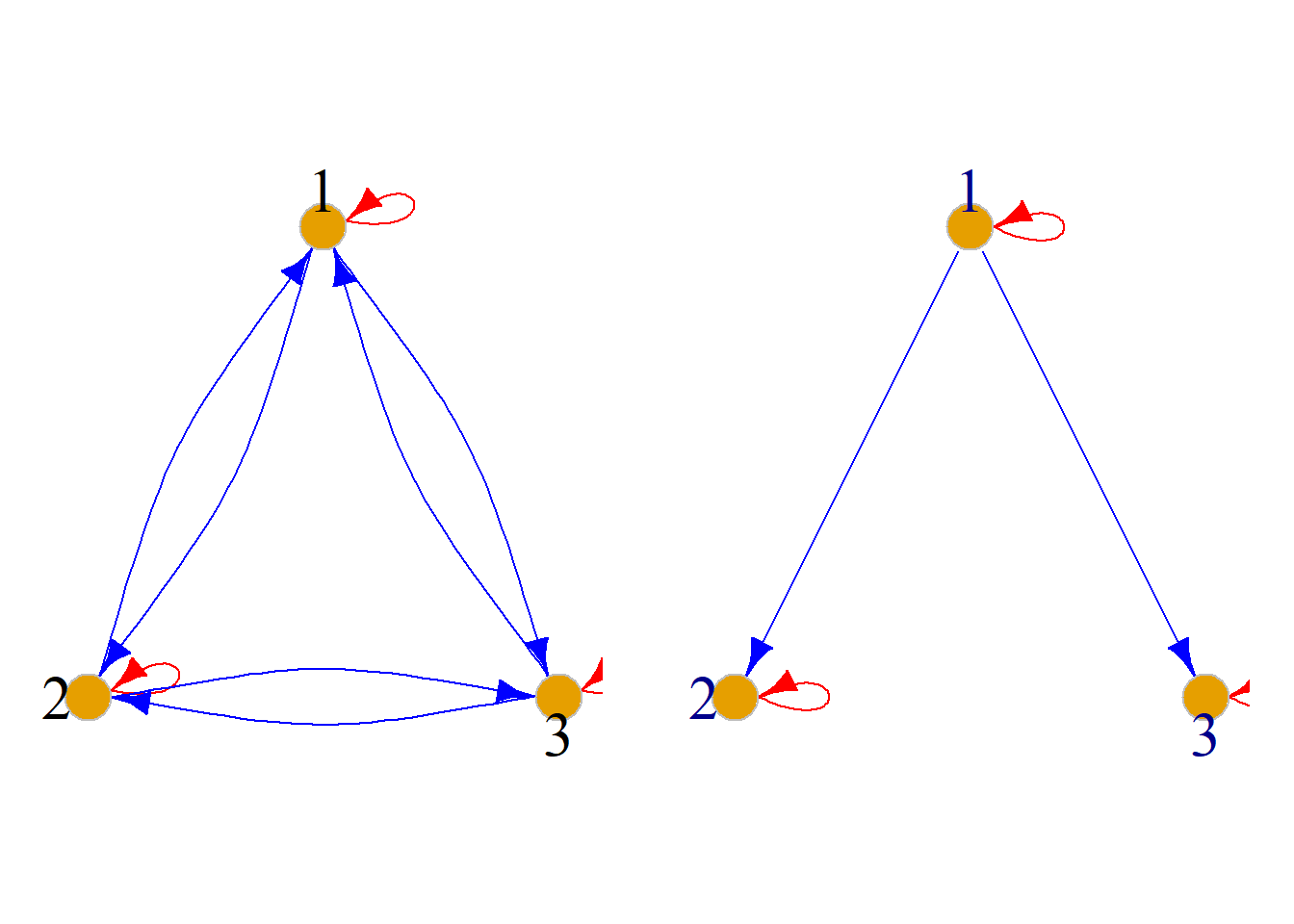
例: 设\(X=\{1, 2, 3\}\), \(X\)上二元关系如下, 画出关系图.

二元关系为: \[E_X, D_X , R=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}1, 3{\rangle}\}\]

对称关系、反对称关系在关系矩阵上的反映:

如果R对称的, 则其关系矩阵为对称矩阵;
如果\(R\)是反对称的, 则其关系矩阵为反对称矩阵. 即:在\(M_R\)中, 若\(m_{ij} =1(i {\neq} j)\)时, \(m_{ji}=0\).

例: 设\(X=\{1, 2, 3\}\), \(X\)上二元关系如下, 给出关系矩阵.

二元关系为: \[E_X, D_X , R=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}1, 3{\rangle}\}\] \[ E_x= \left( \begin{array}{ccc} 1&1&1\\ 1&1&1\\ 1&1&1 \end{array} \right) , \, \, D_{x}= \left( \begin{array}{ccc} 1&1&1\\ 0&1&0\\ 0&0&1 \end{array} \right) ,\,\, R= \left( \begin{array}{ccc} 1&1&1\\ 1&0&0\\ 0&0&0 \end{array} \right). \]

定理: 设\(R\)是集合\(A\)中的二元关系, 则

\(R\)是对称的当且仅当\(R=R^{-1}\).
\(R\)是反对称的当且仅当\(R{\cap}R^{-1}{\subseteq}I_A\).

定理: 设\(R_1\)和\(R_2\)是集合\(A\)中的二元关系, 若\(R_1\), \(R_2\)是对称的, 则 \(R_1^{-1}\)、\(R_1{\cup}R_2\)、\(R_1{\cap}R_2\)也是对称的.

证明: 设\(R_1\)是集合\(A\)中的对称关系. 任取\({\langle}x, y{\rangle}\), 若\({\langle}x, y{\rangle}{\in}R_1^{-1}\), 有\({\langle}y, x{\rangle}{\in}R_1\).

因为\(R_1\)是对称的, 所以\({\langle}x, y{\rangle}{\in}R_1\). 故\({\langle}y, x{\rangle}{\in}R_1^{-1}\), 于是\(R_1^{-1}\)也对称的.

设\(R_1、R_2\)是集合\(A\)中的对称关系.

任取\({\langle}x, y{\rangle}\), 若\({\langle}x, y{\rangle}{\in}R_1{\cup}R_2\), 有:

\({\langle}x, y{\rangle}{\in}R_1\)或 \({\langle}x, y{\rangle}{\in}R_2\).

因为\(R_1\)和\(R_2\)是对称的, 所以

\({\langle}y, x{\rangle}{\in} R_1\)或\({\langle}y, x{\rangle}{\in}R_2\).

故\({\langle}y, x{\rangle}{\in} R_1 {\cup}R_2\).

所以\(R_1{\cup}R_2\)是对称的.

设\(R_1、R_2\)是集合\(A\)中的对称关系.

任取\({\langle}x, y{\rangle}\), 若\({\langle}x, y{\rangle} {\in} R_1 {\cap} R_2\), 有:

\({\langle}x, y{\rangle}{\in} R_1, {\langle}x, y{\rangle}{\in}R_2\).

因为\(R_1\)和\(R_2\)是对称的, 所以:

\({\langle}y, x{\rangle}{\in} R_1, {\langle}y, x{\rangle}{\in}R_2\).

故\({\langle}y, x{\rangle}{\in} R_1 {\cap} R_2.\)

所以\(R_1 {\cap} R_2\)是对称的.

定义: 设\(R\)是集合\(X\)中的二元关系, 若对任意的\(x, y, z{\in}X\), 当\({\langle}x, y{\rangle}{\in}R\)且\({\langle}y, z{\rangle}{\in}R\)时, 有 \({\langle}x, z{\rangle}{\in}R\), 则称关系\(R\)在\(X\)上是传递关系.

例:

集合间的包含”\({\subseteq}\)“关系
数之间的小于”\(<\)“关系
平面几何中三角形之间的”相似”关系

定理: 设\(R\)是集合\(A\)中的二元关系, 则\(R\)是传递的当且仅当\(R{\cdot}R{\subseteq}R\).

例: \(E_x, I_x, D_x, L_x, L_{x^\prime}\)都是传递关系.

因为: \[E_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 1{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

有: \(E_X{\cdot} E_X = E_X\), \(E_X{\cdot} E_X {\subseteq} E_X. 故E_x\)是传递关系.

\[I_x=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

有: \(I_x{\cdot} I_x = I_x\), \(I_x{\cdot} I_x {\subseteq} I_x\). 故\(I_x\)是传递关系.

\[D_x=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

\[D_x{\cdot} D_x=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

有: \(D_x{\cdot} D_x = D_x\), \(D_x{\cdot} D_x {\subseteq} D_x\), 故\(D_x\)是传递关系.

\[L_X=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\] \[L_X{\cdot}L_X = \{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\] 有: \(L_X{\cdot} L_X = L_X\), \(L_X{\cdot} L_X {\subseteq} L_X\), 故\(L_X\)是传递关系.

\[L_{X^\prime}=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\]

\[ L_{X^\prime}{\cdot} L_{X^\prime}=\{{\langle}1, 3{\rangle}\}\] 有: \(L_{X^\prime}{\cdot} L_{X^\prime}{\subseteq} L_{X^\prime}\), 故\(L_{X^\prime}\)是传递关系.

例: \(R_1=\{{\langle}2, 3{\rangle}, {\langle}1, 3{\rangle}\}\)是传递关系.

因为\[R_1 {\cdot} R_1 = \{{\langle}2, 3{\rangle}, {\langle}1, 3{\rangle}\} {\cdot} \{{\langle}2, 3{\rangle}, {\langle}1, 3{\rangle}\} = {\Phi}\]

显然\(R_1 {\cdot} R_1 {\subseteq} R_1\)

故\(R_1\)是传递关系.

\(R_2=\{{\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}, {\langle}1, 3{\rangle}\}\)不是传递关系.

因为: \({\langle}2, 3{\rangle}{\in}R_2, {\langle}3, 2{\rangle}{\in}R_2\), 但\({\langle}2, 2{\rangle}{\in} R_2\),

即: \(R_2{\cdot} R_2 {\nsubseteq} R_2\).

例: 设 \(X=\{1, 2, 3\}\), 给出几个\(X\)上的传递关系.

解: \[R_1=\{{\langle}1, 1{\rangle}\}\] \[R_2=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}1, 3{\rangle}\}\] \[R_3=\{{\langle}1, 3{\rangle}, {\langle}2, 3{\rangle}\}\] 都是\(X\)上的传递关系.

而 \[R_4=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}\}\] \[R_5=\{{\langle}1, 3{\rangle}, {\langle}3, 1{\rangle}\}\] 都不是传递关系.

传递关系在关系图上的反映:

如果\(R\)是传递的, 则其关系图中, 若\(x_i\)到\(x_k\)有有向边, 且\(x_k\)到\(x_j\)有有向边, 则

\(x_i\)到\(x_j\)有有向边.

传递关系在关系矩阵上的反映:

如果\(R\)是传递的, 则:

在矩阵\(M_R= (m_{ij})_{n{\times}n}\)和\(M_R{\cdot}M_R=(b_{ij})_{n{\times}n}\)中, 若\[b_{ij} =1, \] 则有\[m_{ij} =1, \] 其中, \(i, j=1, 2, {\cdots}, n\).

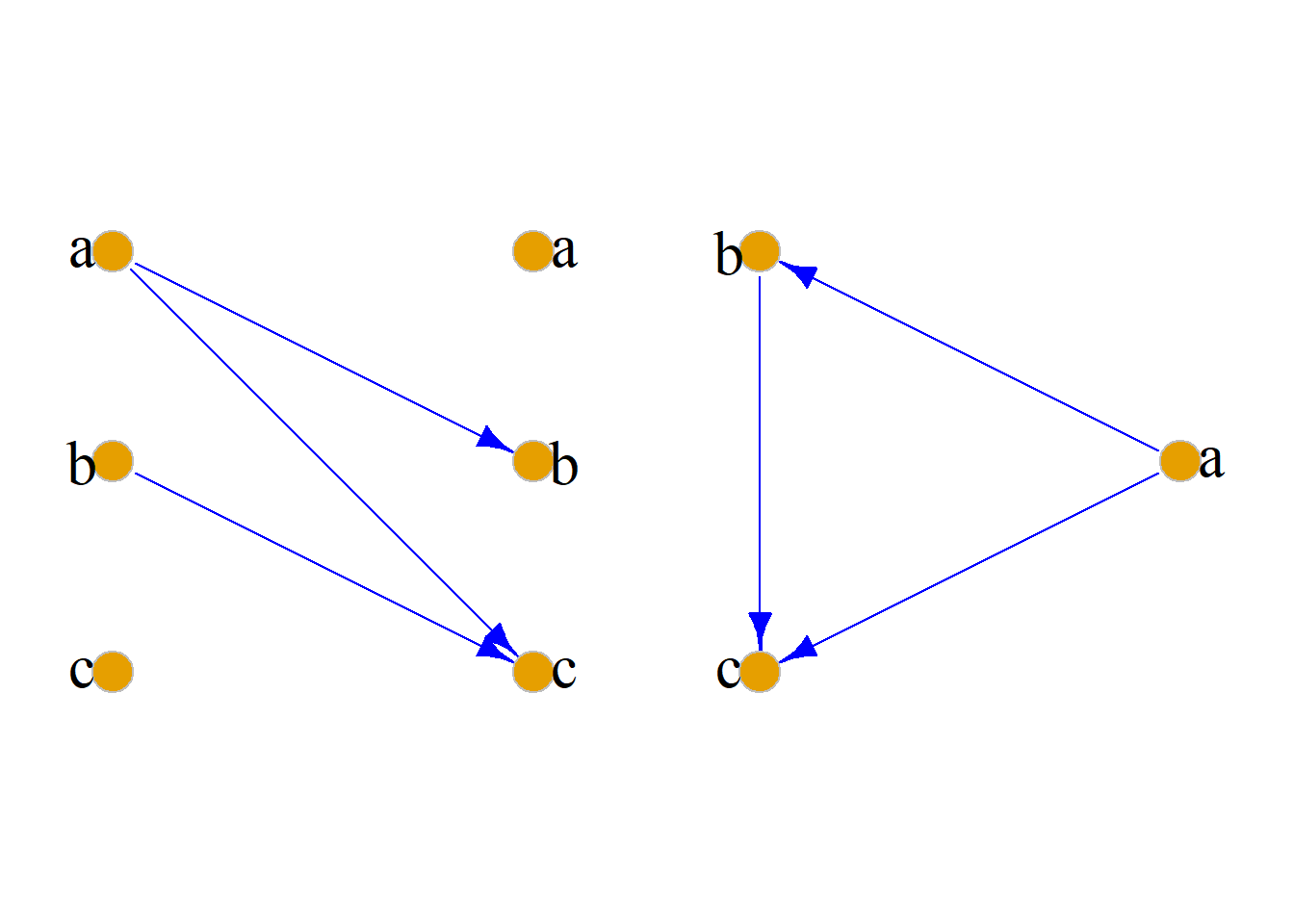
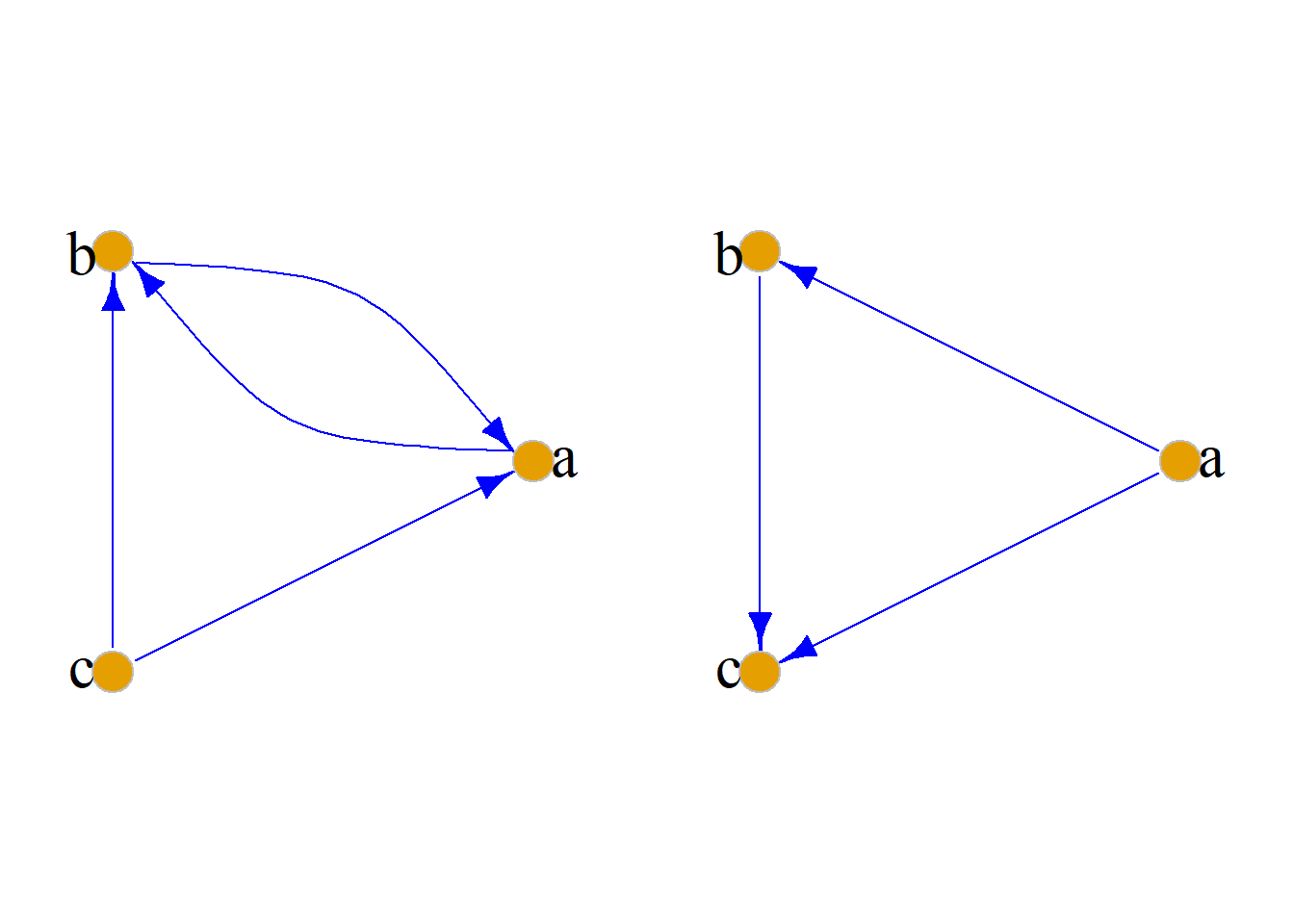
设\(R_1\)和\(R_2\)是\(X=\{a, b, c\}\)上的二元关系, 其关系图如下, 判断它们是否具有传递性.

解: \(R_1\)不是传递的, 因为有\(a{\rightarrow}b\)和\(b{\rightarrow}a\)的有向线段, 但没有\(a{\rightarrow}a\)的有向线段.

\(R_2\)是传递的, 有\(a{\rightarrow}b\)和\(b{\rightarrow}c\)的有向线段, 也有\(a{\rightarrow}c\)的有向线段, 故\(R_2\)是传递的.

实际上, \[R_2 =\{{\langle}a, b{\rangle}, {\langle}b, c{\rangle}, {\langle}a, c{\rangle}\}, \] \[R_2 {\cdot} R_2 =\{{\langle}a, c{\rangle}\} {\subseteq} R_2.\]

也可通过关系矩阵判断.

\[ M_{R_1}= \left( \begin{array}{ccc} \boxed{0}&1&0\\ 1&0&0\\ 1&1&0 \end{array} \right) \] \[ M_{R_1\cdot R_1}= \left( \begin{array}{ccc} \boxed{1}&0&0\\ 0&1&0\\ 1&1&0 \end{array} \right) \]

可见\(b_{11}=1\), 但 \(m_{11}=0\).

\[ M_{R_2}= \left( \begin{array}{ccc} 0&1&\boxed{1}\\ 0&0&1\\ 0&0&0 \end{array} \right) \] \[ M_{R_2\cdot R_2}= \left( \begin{array}{ccc} 0&0&\boxed{1}\\ 0&0&0\\ 0&0&0 \end{array} \right) \]

\(b_{13}=1\), \(m_{13}=1\), 所以是传递的.

定理: 设\(R_1\)和\(R_2\)是集合\(A\)中的二元关系, 若\(R_1\), \(R_2\)是传递的, 则\(R_1^{-1}\)、\(R_1{\cap}R_2\)也是传递的. 但\(R_1{\cup}R_2\)不一定是传递的.

证明: 设\(R_1\)是集合\(A\)中的传递关系.

任意\(x, y, z{\in}A\), 若\({\langle}x, y{\rangle}, {\langle}y, z{\rangle}{\in} R_1^{-1}\), 则

\({\langle}y, x{\rangle}, {\langle}z, y{\rangle}{\in}R_1\), 即\({\langle}z, y{\rangle} , {\langle}y, x{\rangle}{\in}R_1.\)

有\({\langle}z, x{\rangle}{\in} R_1\), 故: \({\langle}x, z{\rangle}{\in} R_1^{-1}\).

所以\(R_1^{-1}\)是传递的.

设\(R_1\), \(R_2\)是集合\(A\)中的传递关系.

任意\(x, y, z{\in}A\), 若\({\langle}x, y{\rangle}, {\langle}y, z{\rangle}{\in} R_1{\cap}R_2\), 则

\[{\langle}x, y{\rangle}, {\langle}y, z{\rangle}{\in}R_1, {\langle}x, y{\rangle}, {\langle}y, z{\rangle}{\in}R_2.\]

因为\(R_1\), \(R_2\)是传递的, 有 \[{\langle}x, z{\rangle}{\in} R_1, {\langle}x, z{\rangle}{\in} R_2.\] 故: \({\langle}x, z{\rangle}{\in}R_1{\cap}R_2\).

所以\(R_1{\cap}R_2\)是传递的.

例: 设\(A=\{a, b, c\}\), 集合\(A\)上传递关系: \[R_1=\{{\langle}a, b{\rangle}, {\langle}b, c{\rangle}, {\langle}a, c{\rangle}\}\] \[R_2=\{{\langle}b, c{\rangle}, {\langle}c, a{\rangle}, {\langle}b, a{\rangle}\}\] 显然: \[R_1{\cup}R_2 =\{{\langle}a, b{\rangle}, {\langle}b, c{\rangle}, {\langle}a, c{\rangle}, {\langle}b, c{\rangle}, {\langle}c, a{\rangle}, {\langle}b, a{\rangle}\}\] 不是传递的.

因为\({\langle}a, b{\rangle}{\in}R_1{\cup}R_2, {\langle}b, a{\rangle}{\in}R_1{\cup}R_2\), 但 \({\langle}a, a{\rangle}{\notin} R_1{\cup}R_2.\)

例: 设\(A=\{1, 2, 3, 4\}\), \(A\)上的二元关系: \[R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 1{\rangle}, \] \[{\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\] 讨论\(R\)的性质(自反性, 对称性和传递性).

解: \(R\)的关系矩阵如下: \[ M_{R}= \left( \begin{array}{cccc} 1&0&1&0\\ 0&1&0&0\\ 1&0&1&1\\ 0&0&1&1 \end{array} \right) \]

\(M_R\)的对角线均为1, 所以\(R\)是自反的;

\(M_R\)是对称矩阵, 所以\(R\)是对称的.

\[ M_{R}=(m_{ij})_{4\times 4}= \left( \begin{array}{cccc} 1&0&1&\boxed{0}\\ 0&1&0&0\\ 1&0&1&1\\ 0&0&1&1 \end{array} \right) \] \[ M_{R\cdot R}=(b_{ij})_{4\times 4}= \left( \begin{array}{cccc} 1&0&1&\boxed{1}\\ 0&1&0&0\\ 1&0&1&1\\ 1&0&1&1 \end{array} \right) \]

\(b_{14}=1\), 但\(m_{14}=0\), 所以\(R\)不是传递的.

关系的闭包

定义: 设集合\(X\), \(R\)是\(X\)中的二元关系, 若有另一个二元关系\({R^\prime}\)满足:

\({R^\prime}\)是自反的 (对称的、传递的)
\(R {\subseteq} {R^\prime}\)
对于任何一个自反的(对称的, 传递的)二元关系\(R^{\prime\prime}\), 如果有\(R{\subseteq}R^{\prime\prime}\), 就有\({R^\prime}{\subseteq}R^{\prime\prime}\), 则称\({R^\prime}\)为\(R\)的自反闭包(closures) (对称闭包, 传递闭包), 记作\(r(R)(s(R), t(R))\).

定理: 设\(R\)是集合\(X\)中的二元关系, \(I_x\)是\(X\)上的恒等关系, \(R^{-1}\)是\(R\)的逆关系, 则

\(r(R)=R{\cup}I_x\)
\(s(R)=R{\cup}R^{-1}\)
\(t(R)=R{\cup}R^2{\cup}R^3{\cup} \cdots =\cup_{i=1}^\infty R^i\)

例: 设\(X=\{1, 2, 3, 4\}\), \(R\)是\(X\)中的二元关系, 并且 \(R=\{{\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 4{\rangle}\}\). 求\(R\)的自反闭包、对称闭包和传递闭包.

解: 自反闭包: \[r(R)=R{\cup}I_x =\{{\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 4{\rangle}\}{\cup} \{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}4, 4{\rangle}\}\] \[=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 4{\rangle}\}\]

对称闭包: \[s(R)=R{\cup}R^{-1} = \{{\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 4{\rangle}\} {\cup} \{{\langle}2, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}3, 2{\rangle}, {\langle}4, 3{\rangle}\}\] \[= \{{\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 3{\rangle}\}\]

传递闭包: \[t(R)=R{\cup}R_2{\cup}R_3{\cup}R_4{\cup}\cdots\] 因为\[R^2=R{\cdot}R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 4{\rangle}\}\] \[R^3=R^2{\cdot}R=\{{\langle}1, 2{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 3{\rangle}\}\] \[R^4=R^3{\cdot}R=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 4{\rangle}\}\] 所以 \[t(R)=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 4{\rangle}\}\]

定理: 设\(R\)是集合\(X\)中的二元关系, 则

\(R=r(R)\), 当且仅当\(R\)是自反的;
\(R=s(R)\), 当且仅当\(R\)是对称的;
\(R=t(R)\), 当且仅当\(R\)是传递的.

引理:若\(R\)和\(S\)都是对称的, 则\(R{\cup}S\)也是对称的.

引理:若\(R\)是对称的, 则\(R^n\)也是对称的, \(n\)为任意正整数.

定理: 设\(R\)是集合\(X\)中的二元关系, 则

若\(R\)是自反的, 则\(s(R)\)和\(t(R)\)也是自反的;
若\(R\)是对称的, 则\(r(R)\)和\(t(R)\)也是对称的;
若\(R\)是传递的, 则\(r(R)\)也是传递的.

定理: 设\(R\), \(S\)都是集合\(X\)上的二元关系, 并且\(R{\subseteq}S\), 则

\(r(R) {\subseteq} r(S)\);
\(s(R) {\subseteq} s(S)\);
\(t(R) {\subseteq} t(S)\).

等价关系

定义: 设\(R\)是定义在集合\(X\)上的二元关系, 若\(R\)是自反的、对称的和传递的, 则称\(R\)是等价关系(Equivalence Relation).

例: 设\(X=\{1, 2, 3, 4\}\), \(X\)上的关系:

试证明\(R\)是\(X\)上的等价关系.

证明: \(R\)的关系矩阵如下:

\[ M_R= \left( \begin{array}{cccc} 1&0&0&1\\ 0&1&1&0\\ 0&1&1&0\\ 1&0&0&1 \end{array} \right) \]

显然, \(M_R\)的主对角线均为1, 故\(R\)是自反的. \(M_R\)是对称矩阵, 故\(R\)是对称的.

\[ M_{R\cdot R}= \left( \begin{array}{cccc} 1&0&0&1\\ 0&1&1&0\\ 0&1&1&0\\ 1&0&0&1 \end{array} \right) =M_R \]

故\(R\)是传递的. 于是\(R\)是等价关系.

例: 设\(X=\{1, 2, 3\}\), \(X\)上的关系 \(R=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\)是等价关系.

例: 设\(X=\{1, 2, 3\}\), \(E_X\)、\(I_x\)是\(X\)上的等价关系.

定义: 设整数集合\(Z\), \(R\)是\(Z\)上的一个二元关系, \(m\)是某个正整数, 若 \[R=\{{\langle}x, y{\rangle}|x, y{\in}Z{\, \wedge\, }m|(x-y)\}\] 则称\(R\)是模\(m\)等价关系, 也叫同余关系(Congruence Relation), 记作: \[x{\equiv}y(mod\, m).\] 同余关系是等价关系, 但等价关系不都是同余关系.

例: 设\(X=\{1, 2, 3, 4, 5, 6, 7\}\), \(R\)是\(X\)上的模3同余关系:\[R=\{{\langle}x, y{\rangle}｜x, y{\in}X{\, \wedge\, }3|(x-y)\}.\]验证\(R\)是等价关系.

解: 对于任意的\(x{\in}X\), 都有\(3|(x-x)\), 即\({\langle}x, x{\rangle}{\in} R\), 故\(R\)是自反的;

对于任意的\(x, y{\in}X\), 若\({\langle}x, y{\rangle}{\in}R\), 即\(3|(x-y)\), 则必有\(3|(y-x)\), 即\({\langle}y, x{\rangle}{\in}R\), 故\(R\)是对称的;

对于任意的\(x, y, z{\in}X\), 若\({\langle}x, y{\rangle}{\in}R\), \({\langle}y, z{\rangle}{\in}R\), 即\(3|(x-y)\), \(3|(y-z)\), 则\(3|(x-y)+(y-z)\), 即\(3|(x-z)\), 故\({\langle}x, z{\rangle}{\in}R\), 所以\(R\)是传递的.

因此, \(R\)是等价关系.

定义: 设\(R\)是集合\(X\)中的等价关系, 对于任意的\(x{\in}X\), \[[x]_R=\{y｜y{\in}X{\wedge}{\langle}x, y{\rangle}{\in}R\}\] 称为由\(x\)生成的\(R\)等价类(Equivalence Class).

\(x\)称为\([x]_R\)的一个代表(Representative).

例: 设\(X=\{1, 2, 3, 4\}\), \(X\)上的等价关系:

\[R=\{{\langle}1, 1{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}4, 1{\rangle}, {\langle}4, 4{\rangle}\}\] \(X\)中各元素的等价类是: \[[1]_R=\{1, 4\} , [2]_R=\{2, 3\}, [3]_R=\{2, 3\}, [4]_R=\{1, 4\}.\]

例: 设\(X=\{1, 2, 3\}\), \(X\)上的等价关系\(R=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}\}\), 求\(X\)中各元素的等价类.

解: \([1]_R=\{1\} , [2]_R=\{2, 3\}, [3]_R=\{2, 3\}\)

定理: 设\(R\)是非空集合\(X\)上的一个等价关系, 则对于任意的\(a, b{\in}X\):

\([a]_R{\neq} {\Phi}\) 且\([a]_R {\subseteq} X\)
\({\langle}a, b{\rangle}{\in}R\) 当且仅当 \([a]_R=[b]_R\)
\({\langle}a, b{\rangle}{\notin}R\) 当且仅当 \([a]_R{\cap}[b]_R={\Phi}\)
\(\cup_{x\in X}^{}[x]_R=X\)

定义: 设\(R\)是非空集合\(X\)上的一个等价关系, 则以\(R\)的所有等价类为元素组成的集合称为\(X\)对\(R\)的商集. 记作\(X/R\). 即: \[X/R=\{ [a]_R|a{\in}X\}\] \(X/R\)的基数称为\(R\)的秩.

例: 设\(X=\{a, b, c, d\}\), \(R\)是\(X\)中的等价关系, 且 \[R=\{{\langle}a, a{\rangle}, {\langle}a, b{\rangle}, {\langle}b, a{\rangle}, {\langle}b, b{\rangle}, {\langle}c, c{\rangle}, {\langle}c, d{\rangle}, {\langle}d, c{\rangle}, {\langle}d, d{\rangle}\}\]

求商集\(X/R\)及\(R\)的秩.

解: 因为\([a]_R=\{a, b\}=[b]_R, [c]_R=\{c, d\} =[d]_R\), 所以\(X/R=\{\{a, b\}, \{c, d\}\}\). \(R\)的秩=2.

例: 设\(N\)为自然数集合, \(R\)为N中的模3同余关系, 即: \(R=\{{\langle}x, y{\rangle}｜x, y{\in}N{\, \wedge\, }3|(x-y)\}\). 求\(N/R\)及\(R\)的秩.

解: \[[0]_R=\{0, 3, 6, 9, \cdots \} =[3]_R=[6]_R=[9]_R= \cdots\]

\[[1]_R=\{1, 4, 7, 10, \cdots \} =[4]_R=[7]_R=[10]_R= \cdots\]

\[[2]_R=\{2, 5, 8, 11, \cdots \} =[5]_R=[8]_R=[11]_R= \cdots\]

故\(N/R=\{[0]_R, [1]_R, [2]_R\}\). R的秩=3.

例: 非空集合\(A\)上的全域关系\(E_A\)是\(A\)上的等价关系, 求\(A\)中任一元素\(x\)的等价类.

解: 对于任意的\(x{\in}A\), 有\([x]_R=｛y｜y{\in}A{\wedge}{\langle}x, y{\rangle}{\in}E_A\} =A\), 故\(A/E_A= \{A\}\)

例: 非空集合\(A\)上的恒等关系\(I_A\)是\(A\)上的等价关系, 求\(A\)中任一元素\(x\)的等价类.

解: 对于任意的\(x{\in}A\), 有 \([x]_R=｛y｜y{\in}A{\wedge}{\langle}x, y{\rangle}{\in}I_A\} =\{x\}\), 故\(A/ I_A= \{\{x\}| x{\in}A \}\)

定义: 对于非空集\(S\), 若有集合族\({\pi}=\{S_1, S_2, \cdots , S_n\}\), 使得:

\(S_i {\neq} {\Phi} (i=1, 2, \cdots , n)\)
\(S_i {\subseteq} S (i=1, 2, \cdots , n)\)
\(S_i {\cap} S_j={\Phi} (i, j=1, 2, \cdots , n)\)
\(S_1{\cup}S_2{\cup} ...{\cup}S_n=S\)

则称\({\pi}\)是集合\(S\)的一个划分. \({\pi}\)中的元素\(S_i\)称为划分块.

例: 设集合\(S=\{a, b, c\}\), 对集合族: \[{\pi}_1=\{\{a, b\}, \{b, c\}\}\] \[{\pi}_2=\{\{a\}, \{b, c\}\}\] \[{\pi}_3=\{\{a\}, \{a, b\}\}\] \[{\pi}_4=\{\{a\}, \{b\}, \{c\}\}\] \[{\pi}_5=\{\{a, b, c\}\}\]

显然, \({\pi}_2, {\pi}_4, {\pi}_5\)都是\(S\)的划分, \({\pi}_1\)和\({\pi}_3\)都不是.

定义: 设\(S\)是一个非空集合, \({\pi}=\{S_1, S_2, \cdots , S_n\}\)是\(S\)的一个划分.

若\(n=|S|\), 则称\({\pi}\)是\(S\)的最大划分.

若\(n=1\), 则称\({\pi}\)是\(S\)的最小划分.

例: 上例\(S=\{a, b, c\}\)的三个划分: \[{\pi}_2=\{\{a\}, \{b, c\}\}\] \[{\pi}_4=\{\{a\}, \{b\}, \{c\}\}\] \[{\pi}_5=\{\{a, b, c\}\}\] \({\pi}_4\)是\(S\)的最大划分, \({\pi}_5\)是\(S\)的最小划分.

定义: 设\(A=\{A_1, A_2, \cdots , A_m\}\), \(B=\{B_1, B_2, \cdots , B_n\}\)是非空集合\(S\)的两个划分:

若对任意的\(B_i{\in}B\), 存在一个\(A_j{\in}A\), 使得: \(B_i{\subseteq}A_j\), 则称\(B\)是\(A\)的加细(细分);
若\(B\)是\(A\)的加细且\(B{\neq}A\), 则称\(B\)是\(A\)的真加细.

例: 上例\(S=\{a, b, c\}\)的三个划分:

\({\pi}_2=\{\{a\}, \{b, c\}\}, {\pi}_4=\{\{a\}, \{b\}, \{c\}\}\), \({\pi}_5=\{\{a, b, c\}\}\)

\({\pi}_4\)是\({\pi}_2\)的真加细, \({\pi}_2\)是\({\pi}_5\)的真加细.

定理: 若\(R\)是非空集合\(X\)中的一个等价关系, 则商集\(X/R\)是\(X\)的一个划分.

我们把这种划分称为由等价关系\(R\)诱导出来的划分, 记为\(X_R\).

例: 设\(X=\{1, 2, 3, 4, 5, 6, 7, 8\}\), \(R\)为\(X\)上的模3同余关系, 即: \[R=\{{\langle}x, y{\rangle}｜x, y{\in}X{\wedge}3|(x-y)\}\] 求:

\(X\)中个元素的等价类;
商集\(X/R\)
由等价关系R诱导出的划分\(X_R\).

解: 等价类:

\[[1]_R=\{1, 4, 7\} =[4]_R=[7]_R\] \[[2]_R=\{2, 5, 8\} =[5]_R=[8]_R\] \[[3]_R=\{3, 6\} =[6]_R\]

商集:

\[X/R = \{ [1]_R, [2]_R , [3]_R \} =\{ \{1, 4, 7\}, \{2, 5, 8\}, \{3, 6\} \}\]

由等价关系\(R\)诱导出的划分:

\[X_R = \{ [1]_R, [2]_R , [3]_R \} =\{ \{1, 4, 7\}, \{2, 5, 8\}, \{3, 6\} \}\]

定理: 集合\(A\)中的一个划分\({\pi}\), 确定\(A\)中的一个等价关系, 称为由划分\({\pi}\)诱导出的等价关系, 记为\(R_{\pi}\).

由划分\({\pi}=\{A_1, A_2, \cdots , A_n\}\)诱导的等价关系是:

\[R_{\pi}=A_1{\times}A_1{\cup}A_2{\times}A_2{\cup}\cdots {\cup}A_n{\times}A_n\] 例: 设\(A=\{1, 2, 3, 4, 5, 6, 7\}\), \(A\)的一个划分 \[C=\{\{1, 4, 7\}, \{2, 5\}, \{3, 6\}\}\] 试给出由划分\(C\)所诱导的等价关系\(R_C\).

解: \[R_C=\{1, 4, 7\}\times \{1, 4, 7\}\cup\{2, 5\}\times \{2, 5\}\cup\{3, 6\}\times\{3, 6\}\] \[=\{{\langle}1, 1{\rangle}, {\langle}1, 4{\rangle}, {\langle}1, 7{\rangle}, {\langle}4, 1{\rangle}, {\langle}4, 4{\rangle}, {\langle}4, 7{\rangle}, {\langle}7, 1{\rangle}, \] \[ {\langle}7, 4{\rangle}, {\langle}7, 7{\rangle}{\langle}2, 2{\rangle}, {\langle}2, 5{\rangle}, {\langle}5, 2{\rangle}, {\langle}5, 5{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 6{\rangle}, {\langle}6, 3{\rangle}, {\langle}6, 6{\rangle}\}\] \(R_C\)是由划分\(C\)所诱导的等价关系.

等价关系和划分是一一对应的.

集合\(A\)上不同的等价关系\(R\)确定不同的商集\(A/R\), 进而对应不同的划分\(A_R\).

反之, 任给集合\(A\)的一个划分\({\pi}\), 就可确定\(A\)上的一个等价关系\(R_{\pi}\).

不同的划分确定不同的等价关系.

这些划分与集合\(A\)上等价关系一一对应, 集合\(A\)上的所有等价关系为:

\[R_1=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 1{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}\}\] \[R_2=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}\}\] \[R_3=\{{\langle}1, 1{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 1{\rangle}, {\langle}3, 3{\rangle}\}\] \[R_4=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}2, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\] \[R_5=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}\}\]

定理: 设\(R_1\)和\(R_2\)是等价关系, 则\(R_1 {\cap} R_2\)也是等价关系.

证明: 因为\(R_1\)和\(R_2\)是等价关系, 则\(R_1\)和\(R_2\)是自反的、对称的和传递的.

所以\(R_1 {\cap} R_2\)也是自反的、对称的和传递的, 故\(R_1 {\cap} R_2\)是等价关系.

相容关系

定义: 设\(R\)是X中的二元关系, 若\(R\)是自反的、对称的, 则称\(R\)是相容关系(Tolerance Relation, or Dependency Relation).

若\({\langle}x, y{\rangle}{\in}R\), 称\(x\)和\(y\)是相容的.

例: 设\(X=\{1, 2, 3, 4\}\), \(R\)是\(X\)上的二元关系:

\[R=\{{\langle}1, 1{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 1{\rangle}, {\langle}4, 2{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\]

容易验证\(R\)是自反的、对称的, 故\(R\)是相容关系.

\[ M_R= \left( \begin{array}{cccc} 1&0&0&1\\ 0&1&1&1\\ 0&1&1&1\\ 1&1&1&1 \end{array} \right) \]

定义: 设\(R\)是集合\(X\)中的一个相容关系, \(A{\subseteq }X\), 若\(A\)中任意两个元素都是相容的, 则称\(A\)是由\(R\)产生的相容类.

更进一步, 若\((X-A)\)中没有一个元素能与\(A\)中的所有元素相容, 则称\(A\)为最大相容类(极大相容类).

在前例中: \(R=\{{\langle}1, 1{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 1{\rangle}, {\langle}4, 2{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\)、\(\{1, 4\}\)、\(\{2, 3, 4\}\)、\(\{2, 4\}\)、\(\{3, 4\}\)、\(\{1\}\)等是相容类.

其中\(\{1, 4\}, \{2, 3, 4\}\)等是最大相容类.

对于\(X\)上的相容关系\(R\), 可以从它的关系图中得到\(R\)的最大相容类.

简化相容关系的关系图:

去掉图中的所有环.
用一条连接两点的线段代替两点之间的双向边.

在一个简化的相容关系的关系图中, 含有\(n\)个结点的最大相容类的任何一个结点与这个类中的其他\(n-1\)个几点都是有边相连.

而类外中的任何结点不可能与类的所有结点相连, 我们把这\(n\)个结点及其关联的边构成的图称为\(G\)的极大完全子图.

可以从相容关系的简化关系图中很方便地求得最大相容类.

在简化图中:

一个极大完全子图的结点集合是一个最大相容类.
一个孤立结点是一个最大相容类;
不在极大完全子图中的边, 其两个端点的集合, 也是一个最大相容类.

例: 给定一个相容关系, 求最大相容类.

From {b}, {a, c}, {c, e, f}, {c, d, f, g} To {a, d, c}, {e, d}, {b, e}, {b, c}

设\(R\)是集合\(X\)上相容关系, \(X\)关于\(R\)的最大相容类具有以下特点:

每个最大相容类都是\(X\)的非空子集;
不同的最大相容类是可以相交的;
所有的最大相容类的并集等于\(X\).

定义: 任意给定一个非空集合\(S\), 若有集合族\({\pi}=\{S_1, S_2, \cdots , S_n\}\), 使得:

\(S_i{\neq} {\Phi} (i=1, 2, \cdots , n)\)
\(S_i{\subseteq}S (i=1, 2, \cdots , n)\)
\(S_1{\cup}S_2{\cup} {\cdots}{\cup}S_n=S\)

则称集合族\({\pi}\)是集合\(S\)的一个覆盖, \(S_i\)称为覆盖块.

注意与划分和划分块比较.

定义: 对于非空集\(S\), 若有集合族\({\pi}=\{S_1, S_2, \cdots , S_n\}\), 使得:

\(S_i {\neq} {\Phi}\)
\(S_i {\subseteq} S\)
\(S_i {\cap} S_j={\Phi}\)
\(S_1{\cup}S_2{\cup} {\cdots}{\cup}S_n=S\)

则称\({\pi}\)是集合\(S\)的一个划分.\({\pi}\)中的元素\(S_i\)称为划分块.

例: 设集合\(S=\{a, b, c\}\), 若 \[{\pi}_1=\{\{a\}, \{a, b\}, \{b, c\}\}\] \[{\pi}_2=\{\{a, c\}, \{b, c\}\}\] \[{\pi}_3=\{\{a, b, c\}\}\] \[{\pi}_4=\{\{a\}, \{a, b\}, \{b\}\}\] 则\({\pi}_1、{\pi}_2、{\pi}_3\)都是\(S\)的覆盖, \({\pi}_4\)不是.

定义: 设\(S=\{S_1, S_2, \cdots, S_n\}\)是集合\(A\)的一个覆盖, 若对任意的\(S_i{\in}S\), 不存在\(S\)中其它元素\(S_j\), 使得\(S_i{\subseteq}S_j\), 则称\(S\)是\(A\)的一个完全覆盖.

例: 设集合\(S=\{a, b, c\}\), 若 \[{\pi}_1=\{\{a\}, \{a, b\}, \{b, c\}\}\] \[{\pi}_2=\{\{a, c\}, \{b, c\}\}\] \[{\pi}_3=\{\{a, b, c\}\}\] 则\({\pi}_1、{\pi}_2、{\pi}_3\)都是\(S\)的覆盖. \({\pi}_2\), \({\pi}_3\)都是\(S\)的完全覆盖.

定理: 若\(R\)是集合\(X\)上的相容关系, 则\(X\)关于\(R\)的所有最大相容类的集合是\(X\)的一个覆盖(完全覆盖), 称为由相容关系\(R\)诱导出的覆盖(完全覆盖), 记为\(X_R\).

定理: 给定集合\(A\)的一个覆盖\({\pi}=\{A_1, A_2, \cdots , A_n\}\), 则由覆盖\({\pi}\)确定的关系\(R=A_1{\times}A_1{\cup}A_2{\times}A_2{\cup}\cdots {\cup}A_n{\times}A_n\)是一个相容关系.

例: 设\(X=\{1, 2, 3, 4\}\), \(X_1\)和\(X_2\)是\(X\)的两个不同的覆盖:

\[X_1=\{ \{1\}, \{2, 3, 4\} \}\] \[X_2=\{ \{1\}, \{2, 3\}, \{2, 4\}, \{3, 4\} \}\]

试给出分别由\(X_1\)和\(X_2\)所确定的相容关系.

解: 分别由\(X_1\)和\(X_2\)所确定的相容关系:

\[R_1=\{1\}{\times}\{1\}{\cup}\{2, 3, 4\}{\times}\{2, 3, 4\}\] \[=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 2{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\]

\[X_2=\{ \{1\}, \{2, 3\}, \{2, 4\}, \{3, 4\} \}\] \[R_2=\{1\}{\times}\{1\}{\cup}\{2, 3\}{\times}\{2, 3\}{\cup}\{2, 4\}{\times}\{2, 4\}{\cup}\{3, 4\}{\times}\{3, 4\}\] \[=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 2{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\] \[R_1=\{{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 2{\rangle}, {\langle}4, 3{\rangle}, {\langle}4, 4{\rangle}\}\] 这个例子说明, 不同的覆盖可能产生相同的相容关系.

例: 设\(X=\{216, 243, 375, 455, 648\}\), 相容关系:

\(R=\{{\langle}x, y{\rangle}|x, y{\in}X{\wedge}x, y\)有相同数字\(\}\),

求最大相容类及由此产生的\(X\)的完全覆盖.

解: 用\(x_1, x_2, x_3, x_4, x_5\) 分别代表: 216, 243, 375, 455, 648, 则

\[X=\{x_1, x_2, x_3, x_4, x_5\}\]

\[R=\{{\langle}x_1, x_1{\rangle}, {\langle}x_1, x_2{\rangle}, {\langle}x_1, x_5{\rangle}, \] \[{\langle}x_2, x_1{\rangle}, {\langle}x_2, x_2{\rangle}, {\langle}x_2, x_3{\rangle}, {\langle}x_2, x_4{\rangle}, \] \[{\langle}x_2, x_5{\rangle}, {\langle}x_3, x_2{\rangle}, {\langle}x_3, x_3{\rangle}, {\langle}x_3, x_4{\rangle}, \] \[{\langle}x_4, x_2{\rangle}, {\langle}x_4, x_3{\rangle}, {\langle}x_4, x_4{\rangle}, {\langle}x_4, x_5{\rangle}, \] \[{\langle}x_5, x_1{\rangle}, {\langle}x_5, x_2{\rangle}, {\langle}x_5, x_4{\rangle}, {\langle}x_5, x_5{\rangle}\}\]

最大相容类为: \[A_1=\{x_1, x_2, x_5\}, A_2=\{x_2, x_3, x_4\}, A_3=\{x_2, x_4, x_5\}.\] \(X\)的一个完全覆盖: \[{\pi}=\{A_1, A_2, A_3\}=\{\{x_1, x_2, x_5\}, \{x_2, x_3, x_4\}, \{x_2, x_4, x_5\}\}.\]

偏序关系

定义: 设\(R\)是集合\(X\)上的二元关系, 若\(R\)是自反、反对称和传递的, 则称\(R\)是一个偏序关系.

通常用“\({\leq}\)”表示偏序关系, 并把序偶\({\langle}X, {\leq}{\rangle}\)称为偏序集合.

若\({\langle}x, y{\rangle}{\in}R\), 写作\(x{\leq}y\), 读作\(x\)小于等于\(y\).

例:

实数集合中的小于等于关系.
整数集合中的整除关系.
集合之间的包含关系.

例: 自然数\(N\)上的小于等于关系\(R\)是偏序关系.

证明: \[R=\{{\langle}a, b{\rangle}|a, b{\in}N\wedge a{\leq}b\}\]

对任意的\(a{\in}N\), 有\(a{\leq}a\), 故\({\langle}a, a{\rangle}{\in}R\), \(R\)是自反的;
对任意的\(a, b{\in}N\), 若\({\langle}a, b{\rangle}{\in}R\), 且\({\langle}b, a{\rangle}{\in}R\), 即\(a{\leq}b, b{\leq}a\), 有\(a=b\), 故\(R\)是反对称的;
对任意的\(a, b, c{\in}N\), 若\({\langle}a, b{\rangle}{\in}R, {\langle}b, c{\rangle}{\in}R\), 即\(a{\leq}b, b{\leq}c\), 有\(a {\leq} c\), 即\({\langle}a, c{\rangle}{\in}R\), 故\(R\)是传递的;

故\(R\)是偏序关系.

例: \[{\leq}::=R=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, \cdots , {\langle}2, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, \cdots , {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}3, 5{\rangle}, \cdots\}\]

例: 给定集合\(A=\{2, 3, 6, 8\}\): \[R=\{{\langle}a, b{\rangle}|a, b{\in}A\wedge a|b\}\] \(R\)是否是偏序关系？

解: \[R=\{{\langle}2, 2{\rangle}, {\langle}2, 6{\rangle}, {\langle}2, 8{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 6{\rangle}, {\langle}6, 6{\rangle}, {\langle}8, 8{\rangle}\}\]

\[ M_R= \left( \begin{array}{cccc} 1&0&1&1\\ 0&1&1&0\\ 0&0&1&0\\ 0&0&0&1 \end{array} \right),\,\, M_{R\cdot R}= \left( \begin{array}{cccc} 1&0&1&1\\ 0&1&1&0\\ 0&0&1&0\\ 0&0&0&1 \end{array} \right) \]

显然, \(R\)是自反、反对称和传递的, 故\(R\)是偏序关系.

定义: 设\(R\)是集合\(X\)上的二元关系, 若\(R\)是反自反的和传递的, 则称\(R\)是一个严格偏序关系(拟序关系).

通常用”\(<\)“表示严格偏序关系, 并把序偶\({\langle}X, <{\rangle}\)称为严格偏序集合.

若\({\langle}x, y{\rangle}{\in}R\), 写做\(x<y\), 读作\(x\)小于\(y\).

例: 实数集合中的”小于关系”是严格偏序关系, 因为它是反自反和传递的.

例: 自然数\(N\)上的小于关系\(R\)是严格偏序关系.

证明: \(R=\{{\langle}a, b{\rangle}|a, b{\in}N \wedge a<b\}\)

对任意的\(a{\in}N\), 有\(a\nless a\), 故\({\langle}a, a{\rangle}{\notin}R\), \(R\)是反自反的; 对任意的\(a, b, c{\in}N\), 若\({\langle}a, b{\rangle}{\in}R, {\langle}b, c{\rangle}{\in}R\), 即\(a<b, b<c\), 有\(a<c\), 即\({\langle}a, c{\rangle}{\in}R\), 故\(R\)是传递的. 故\(R\)是严格偏序关系.

\[<::=R=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}1, 4{\rangle}, \cdots , {\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}2, 5{\rangle}, \cdots , {\langle}3, 4{\rangle}, {\langle}3, 5{\rangle}, {\langle}3, 6{\rangle}, \cdots , \}\]

定理: 若\(R\)是集合\(A\)上的严格偏序关系, 则\(R\)是反对称的.

证明: 反证法.

假设\(R\)不是反对称的, 即存在\(x, y{\in}A, {\langle}x, y{\rangle}{\in}R, {\langle}y, x{\rangle}{\in}R\), 且\(x{\neq}y\).则由\(R\)的传递性, 有\({\langle}x, x{\rangle}{\in}R\).这与\(R\)是反自反的相矛盾.故\(R\)是反对称的.

偏序关系:自反、反对称、传递

严格偏序关系:反自反、反对称、传递

定义: 设\({\langle}A, {\leq}{\rangle}\)为偏序集, 对于任意的\(x, y{\in}A\), 如果\(x{\leq}y\)或\(y{\leq}x\), 则称\(x\)和\(y\)是可比的.

定义: 在偏序集\({\langle}A, {\leq}{\rangle}\)中, 对于任意的\(x, y{\in}A\), 如果\(x{\leq}y, x{\neq}y\), 而且不存在任何其它元素\(z{\in}A\), 使得\(x{\leq}z\)且\(z{\leq}y\), 则称\(y\)覆盖\(x\).

并记: \(COV_A=\{{\langle}x, y{\rangle}|x, y{\in}A{\wedge}y\)覆盖\(x\}\) 为覆盖集.

例: 设\({\langle}A, {\leq}{\rangle}\)为偏序集, 其中\(A\)是正整数12的因子集合, 并设\({\leq}\) 为整除关系, 求\(COV_A\).

解: \(A=\{1, 2, 3, 4, 6, 12\}\). \[{\leq}::=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}1, 4{\rangle}, {\langle}1, 6{\rangle}, {\langle}1, 12{\rangle}, {\langle}2, 4{\rangle}, {\langle}2, 6{\rangle}, {\langle}2, 12{\rangle}, {\langle}3, 6{\rangle}, \]

\[{\langle}3, 12{\rangle}, {\langle}4, 12{\rangle}, {\langle}6, 12{\rangle},{\langle}1, 1{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}4, 4{\rangle}, {\langle}6, 6{\rangle}, {\langle}12, 12{\rangle}\}\]

覆盖集为: \[COV_A=\{{\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}2, 6{\rangle}, {\langle}3, 6{\rangle}, {\langle}4, 12{\rangle}, {\langle}6, 12{\rangle}\}\]

下面用哈斯图来描述一个偏序关系, 这是一种简化的关系图.

方法一:对偏序集合\({\langle}A, {\leq}{\rangle}\), 则先求出\(COV_A\)集合, 然后按如下方法构造哈斯图:

用小圆点表示\(A\)中的元素;
若\({\langle}x, y{\rangle}{\in}COV_A\), 即\(y\)覆盖\(x\), 则将\(y\)画在\(x\)的上层, 并在\(x, y\)之间用一条线段相连;
若\(x, y\)之间不可比, 则把\(x, y\)画在同一层上.

特别注意:若有\(x{\leq}y, x{\neq}y\), 但\(y\)不覆盖\(x\), 则\(x\)和\(y\)之间不能有连线.

例: 设\({\langle}A, {\leq}{\rangle}\)为偏序集, 其中\(A=\{1, 2, 3, 4\}\), 设\({\leq}\) 为小于等于关系, 求其哈斯图.

解: \[{\leq}::=\{{\langle}1, 1{\rangle}, {\langle}1, 2{\rangle}, {\langle}1, 3{\rangle}, {\langle}1, 4{\rangle}, {\langle}2, 2{\rangle}, \] \[{\langle}2, 3{\rangle}, {\langle}2, 4{\rangle}, {\langle}3, 3{\rangle}, {\langle}3, 4{\rangle}, {\langle}4, 4{\rangle}\}\]

\[COV_A=\{{\langle}1, 2{\rangle}, {\langle}2, 3{\rangle}, {\langle}3, 4{\rangle}\}\]

例: 设\(X=\{2, 3, 4, 6, 8, 12, 16, 24\}\),

整除关系:

\(R=\{{\langle}x, y{\rangle}｜x, y{\in}X{\wedge} x|y{\in}X\}\)

则\[COV_X=\{{\langle}2, 4{\rangle}, {\langle}2, 6{\rangle}, {\langle}4, 8{\rangle}, {\langle}4, 12{\rangle}, {\langle}8, 16{\rangle}, \] \[ {\langle}8, 24{\rangle}, {\langle}3, 6{\rangle}, {\langle}6, 12{\rangle}, {\langle}12, 24{\rangle}\}\]

方法二: 通过关系图的简化得到哈斯图.

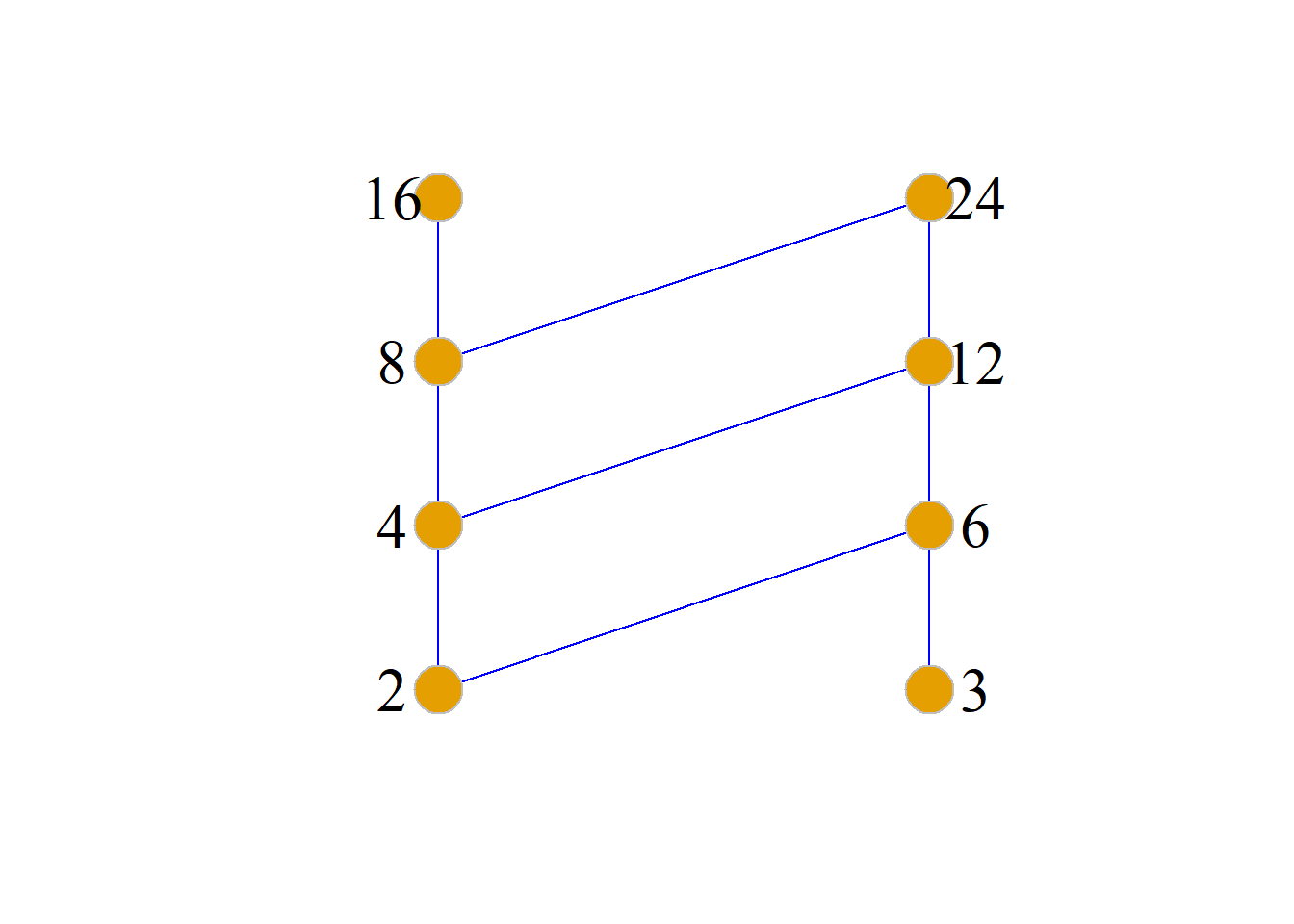
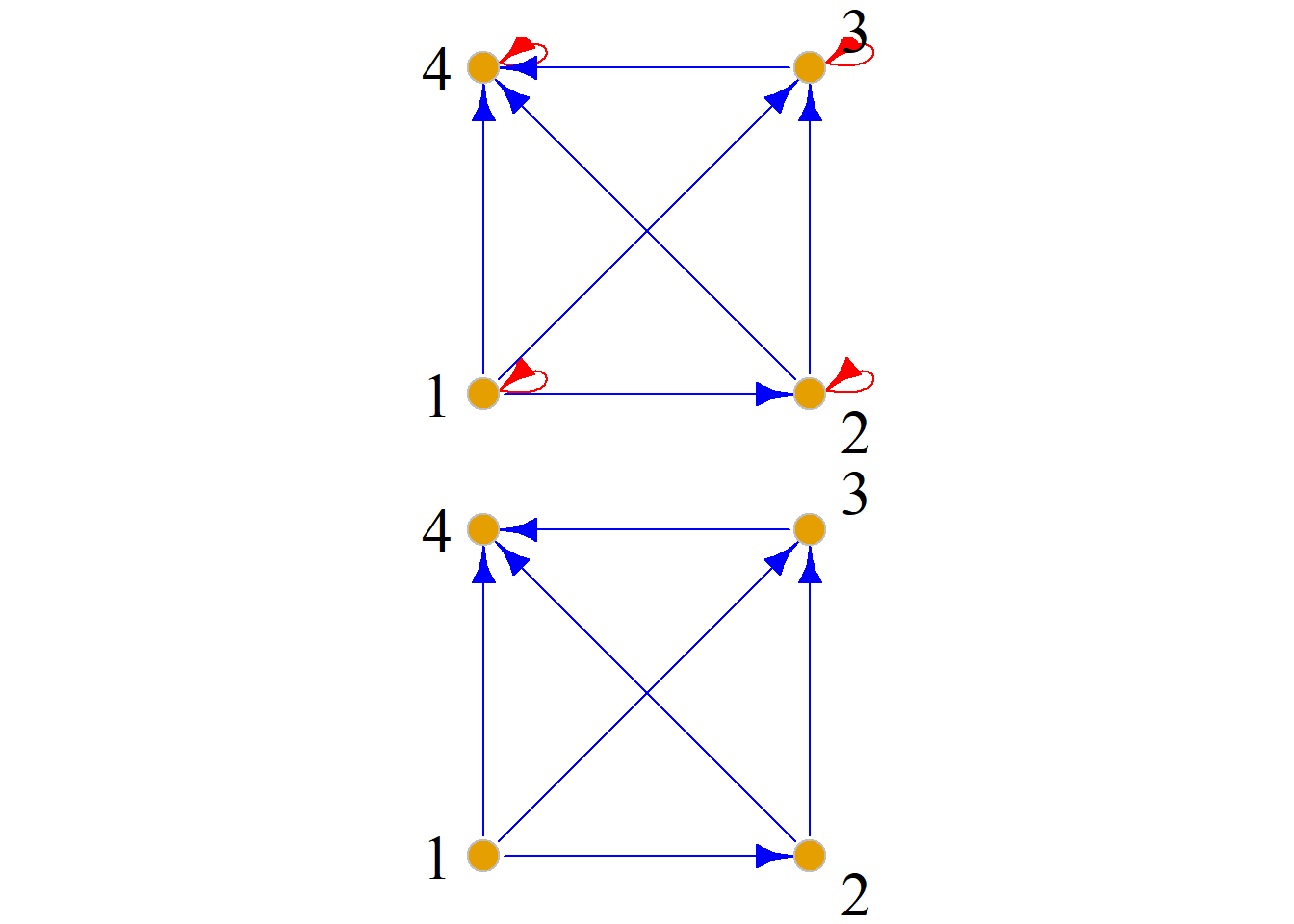
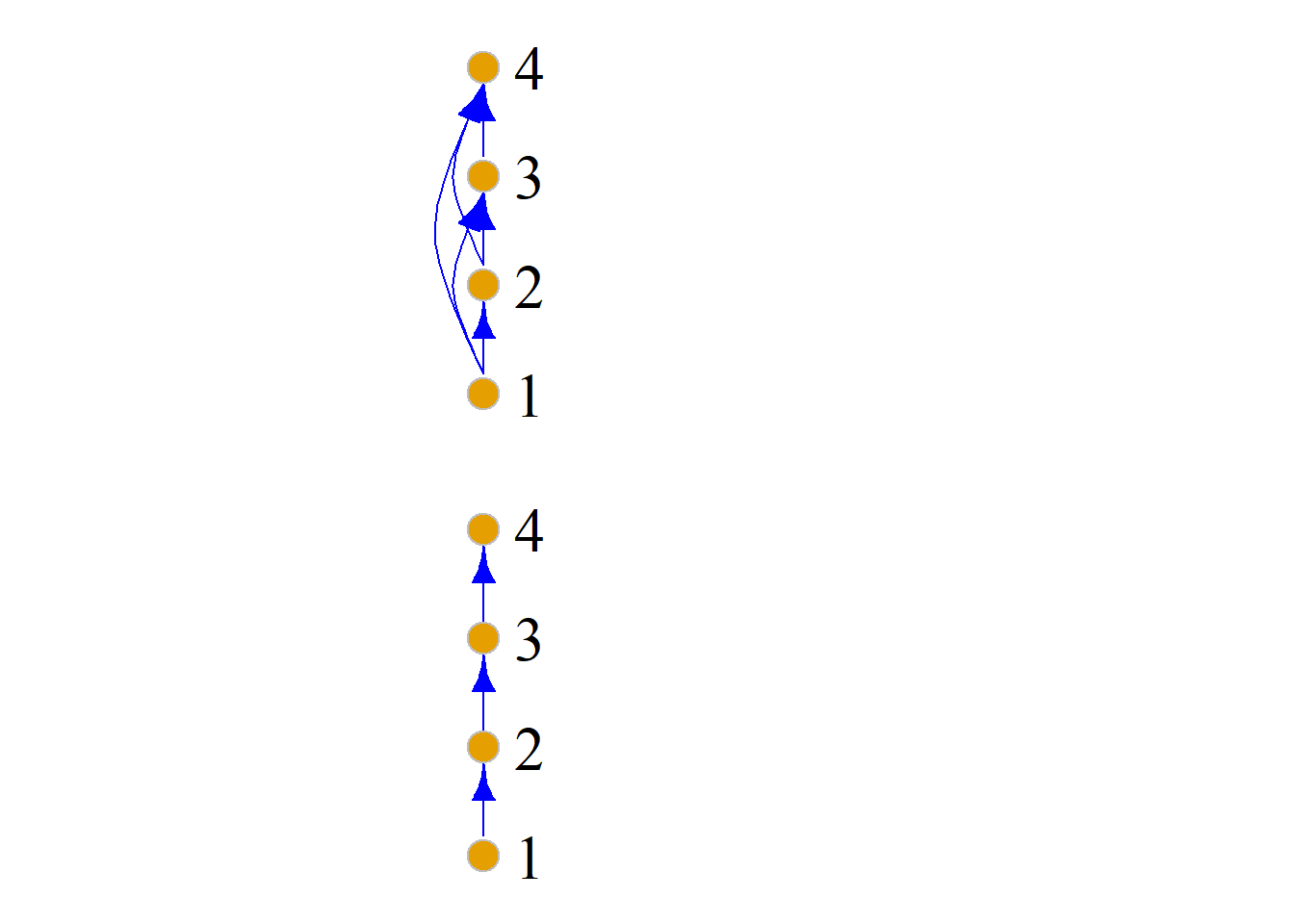
例: 设\(A=\{a, b, c\}\), 求\({\langle}{P}(A), {\subseteq}{\rangle}\)的哈斯图.

解: 因为 \[{P}(A)=\{ {\Phi}, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \}\] \[COV_{P}(A)=\{{\langle}{\Phi}, \{a\}{\rangle}, {\langle}{\Phi}, \{b\}{\rangle}, {\langle}{\Phi}, \{c\}{\rangle}, {\langle}\{a\}, \{a, b\}{\rangle},\]

\[{\langle}\{a\}, \{a, c\}{\rangle}, {\langle}\{b\}, \{a, b\}{\rangle}, {\langle}\{b\}, \{b, c\}{\rangle},\] \[{\langle}\{c\}, \{a, c\}{\rangle}, {\langle}\{c\}, \{b, c\}{\rangle}, {\langle}\{a, b\}, \{a, b, c\}{\rangle},\] \[{\langle}\{a, c\}, \{a, b, c\}{\rangle}, {\langle}\{b, c\}, \{a, b, c\}{\rangle}\}\]

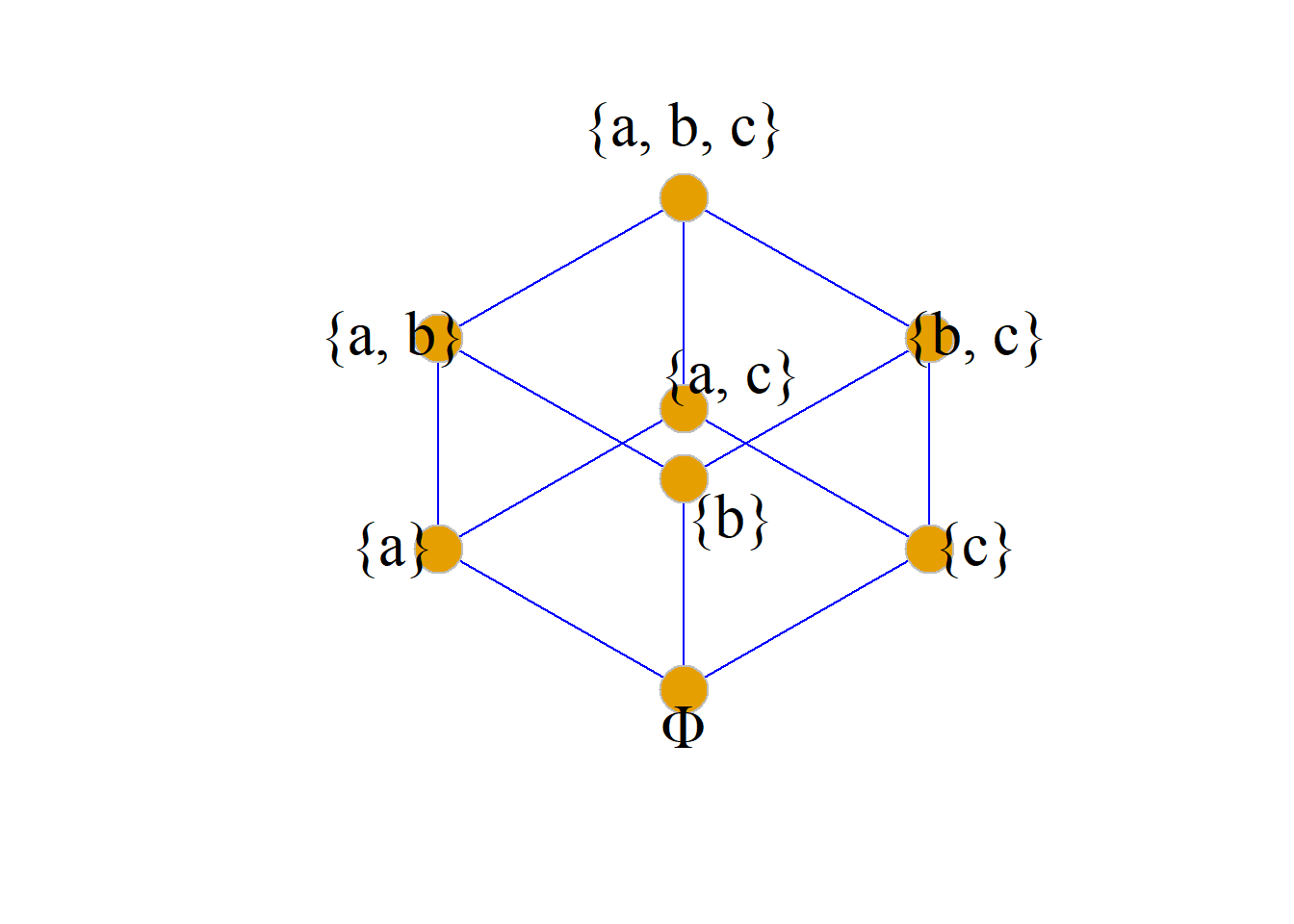
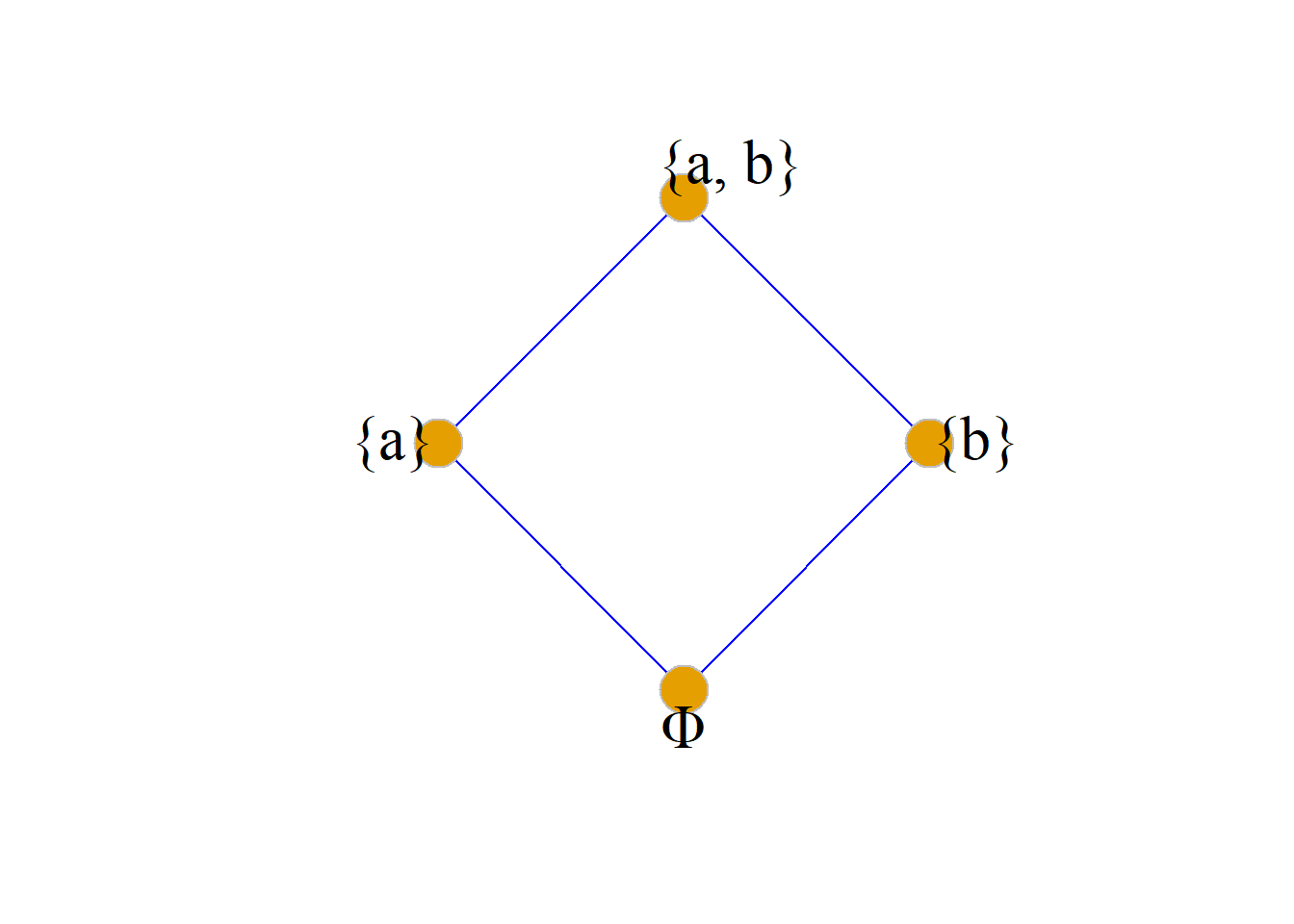
定义: 设\({\langle}A, {\leq}{\rangle}\)是一个偏序集, \(Q{\subseteq}A\).

若存在一个元素\(a{\in}Q\), 使得:

对任意的\(x{\in}Q\), 都有\(a{\leq}x\), 则称\(a\)是\(Q\)的最小元.
对任意的\(x{\in}Q\), 都有\(x{\leq}a\), 则称\(a\)是\(Q\)的最大元.

定义: 设\({\langle}A, {\leq}{\rangle}\)是一个偏序集, \(Q{\subseteq}A\). 若存在一个元素\(a{\in}Q\), 使得:

\(Q\)中无任何其它元素\(x\)能满足\(x{\leq}a\), 则称\(a\)是\(Q\)的极小元.
\(Q\)中无任何其它元素\(x\)能满足\(a{\leq}x\), 则称\(a\)是\(Q\)的极大元.

例: 设\(A=\{a, b\}\), 在偏序集\({\langle}{P}(A), {\subseteq}{\rangle}\)中, 求\(\{{\Phi}, \{a\}\}, \{\{a\}, \{b\}\}\), \(P(A)\)的最大元与最小元.

解: \(P(A)=\{{\Phi}, \{a\}, \{b\}, \{a, b\}\}\), 画出\({\subseteq}\)的哈斯图.

从哈斯图可以看出:

\(\{\Phi, \{a\}\}\)的最大元是{\(a\)}, 最小元是\(\Phi\).
\(\{\{a\}, \{b\}\}\)没有最大元和最小元.
\(P(A)\)的最大元是\(\{a, b\}\), 最小元是\(\Phi\).

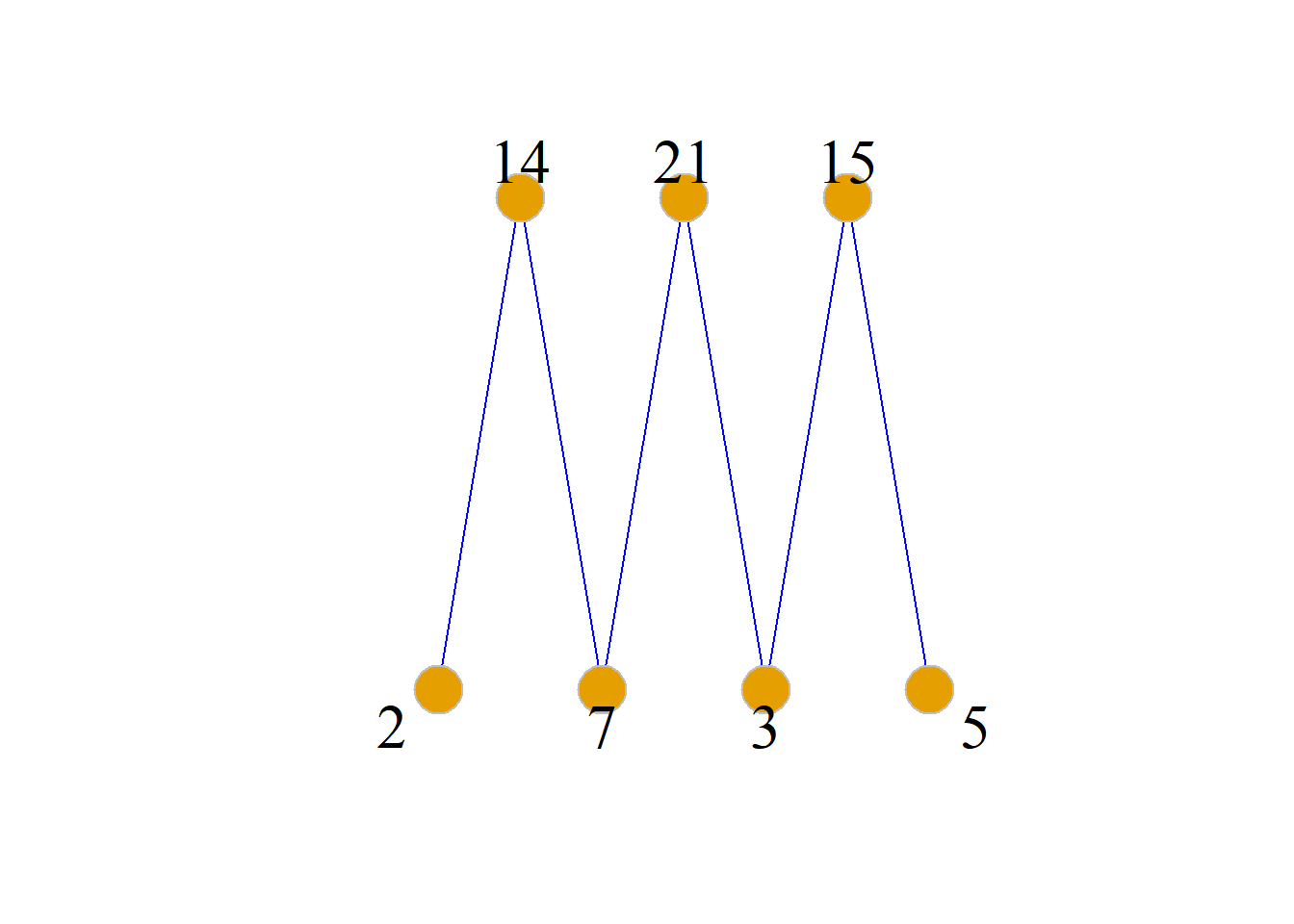
例: 设\(A=\{2, 3, 5, 7, 14, 15, 21\}\), 其上偏序关系 \[R=\{{\langle}2, 14{\rangle}, {\langle}3, 15{\rangle}, {\langle}3, 21{\rangle}, {\langle}5, 15{\rangle}, {\langle}7, 14{\rangle},\] \[{\langle}7, 21{\rangle}, {\langle}2, 2{\rangle}, {\langle}3, 3{\rangle}, {\langle}5, 5{\rangle}, {\langle}7, 7{\rangle}, \] \[{\langle}14, 14{\rangle}, {\langle}15, 15{\rangle}, {\langle}21, 21{\rangle}\}\]

求: \(B=\{2, 7, 3, 21, 14\}\)的极大元、极小元、最大元和最小元.

\(B=\{2, 7, 3, 21, 14\}\)中

极小元: {2, 7, 3}
极大元: {14, 21}
无最小元和最大元.

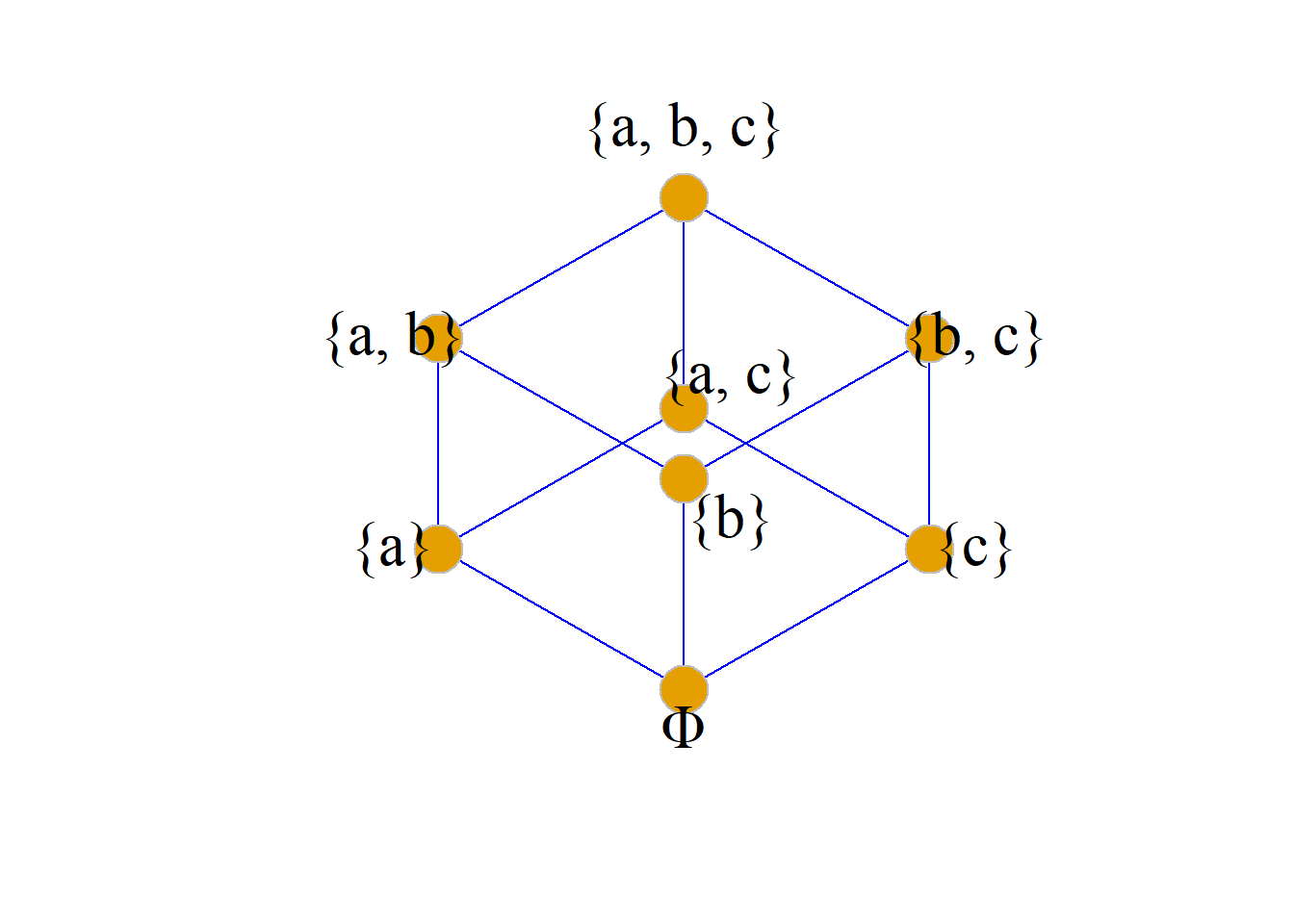
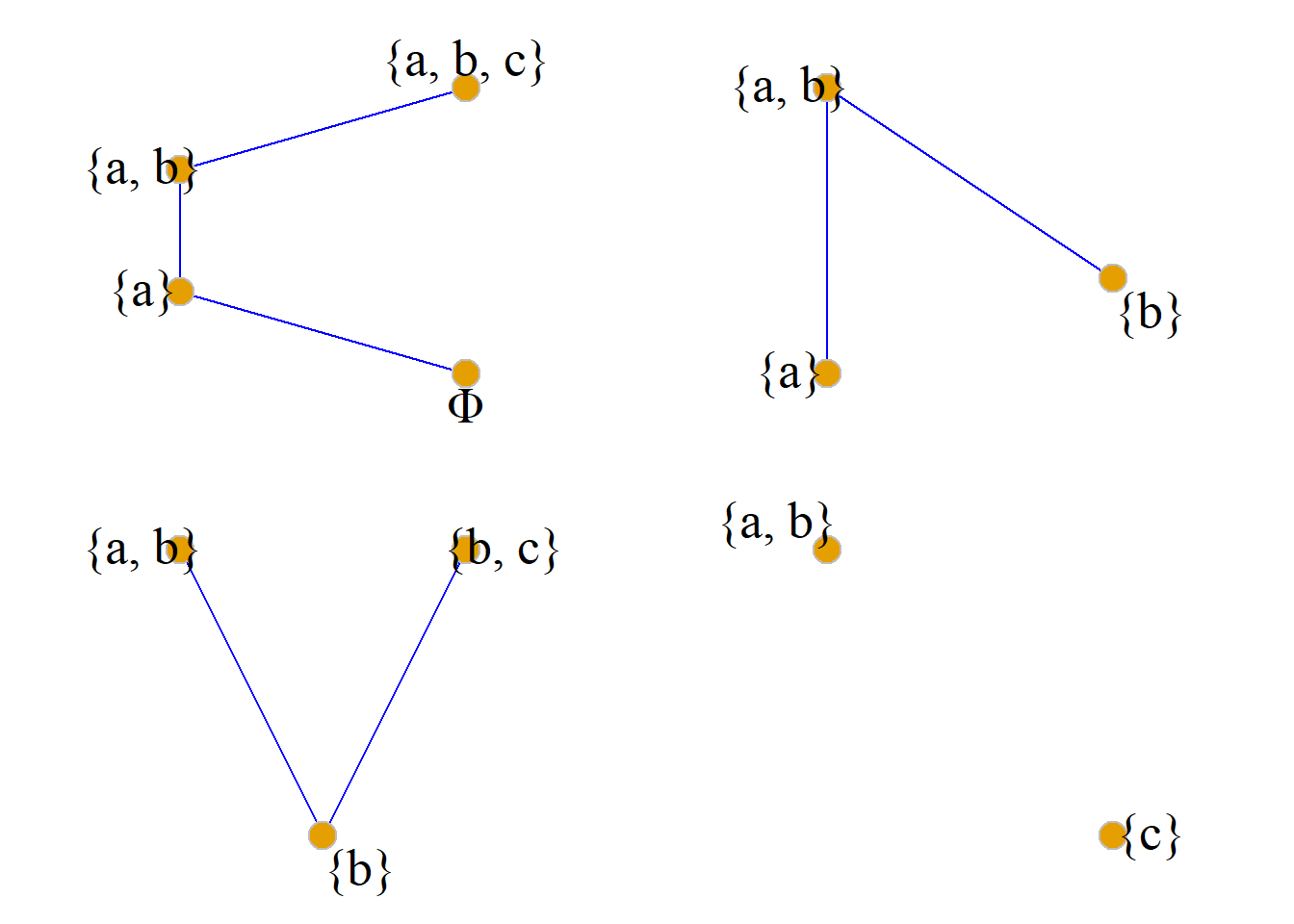
例: 设\(A=\{a, b, c\}\), 在偏序集\({\langle}{P}(A), {\subseteq}{\rangle}\)中, \[P(A)=\{{\Phi}, \{a\}, \{b\}, \{c\}, \] \[\{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}, \] \[Q_1=\{{\Phi}, \{a\}, \{a, b\}, \{a, b, c\}\}, \] \[Q_2=\{\{a\}, \{b\}, \{a, b\}\}, \] \[Q_3=\{\{b\}, \{a, b\}, \{b, c\}\}, \] \[Q_4=\{\{c\}, \{a, b\}\}, \] 求: \(Q_1\)、\(Q_2\)、\(Q_3\)和\(Q_4\)的极大元和极小元.

\[Q_1=\{{\Phi}, \{a\}, \{a, b\}, \{a, b, c\}\}\] \[Q_2=\{\{a\}, \{b\}, \{a, b\}\}\]

\[Q_3=\{\{b\}, \{a, b\}, \{b, c\}\}\]

\[Q_4=\{\{c\}, \{a, b\}\}\] \(Q_1\)的极大元是\(\{a, b, c\}\), 极小元是\(\Phi\).

\(Q_2\)的极大元是\(\{a, b\}\), 极小元是\(\{a\}, \{b\}\).

\(Q_3\)的极大元是\(\{a, b\}, \{b, c\}\), 极小元是\(\{b\}\).

\(Q_4\)的极大元是\(\{a, b\}, \{c\}\), 极小元是\(\{a, b\}, \{c\}\).

定理: 设\({\langle}A, {\leq}{\rangle}\)是偏序集, \(Q\)是\(A\)的一个子集, 则:

若\(Q\)有最小元, 则最小元必是唯一的.
若\(Q\)有最大元, 则最大元必是唯一的.

定义: 设\({\langle}A, {\leq}{\rangle}\)是偏序集, \(Q{\subseteq}A\), 若存在一个元素\(a{\in}A\), 使得:

对任意的\(x{\in}Q\), 都有\(x{\leq}a\), 则称\(a\)是\(Q\)的上界, 记作\(U_B\);
对任意的\(x{\in}Q\), 都有\(a{\leq}x\), 则称\(a\)是\(Q\)的下界, 记作\(L_B\).

定义: 设\({\langle}A, {\leq}{\rangle}\)是偏序集, \(Q{\subseteq}A\), 若存在一个元素\(a{\in}A\), 使得:

\(a\)是\(Q\)的上界, 并且对\(Q\)的每一个上界\(a^\prime\), 都有\(a{\leq}a^\prime\), 则称\(a\)是\(Q\)的最小上界(上确界), 记作\(LU_B\);
\(a\)是\(Q\)的下界, 并且对\(Q\)的每一个下界\(a^\prime\), 都有\(a^\prime{\leq}a\), 则称\(a\)是\(Q\)的最大下界(下确界), 记作\(GL_B\).

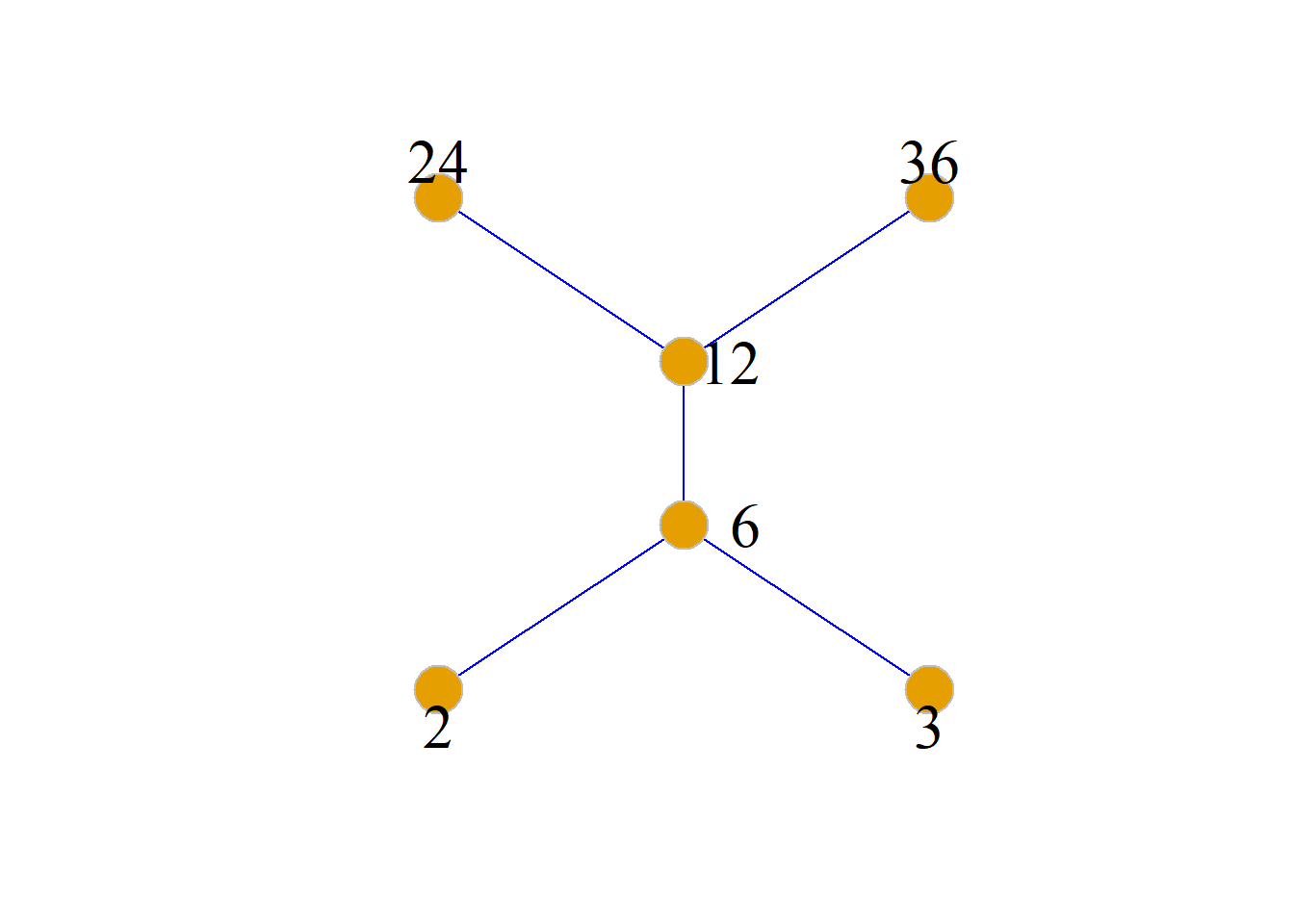
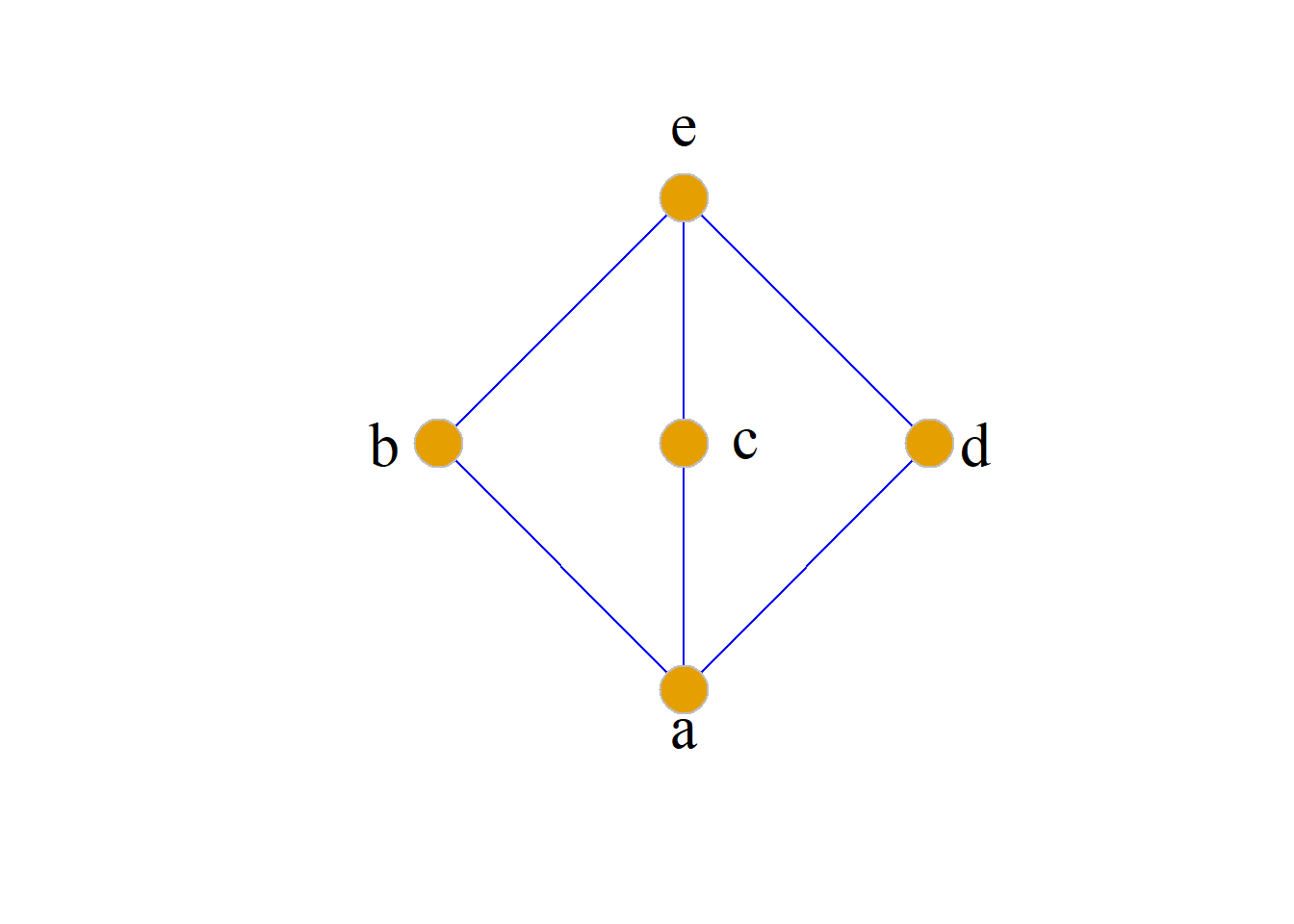
例: 设\(A=\{2, 3, 6, 12, 24, 36\}\), \(A\)上的偏序关系\(R\)的哈斯图如图.

求子集\(\{2, 3, 6\}\)和子集\(\{6, 12\}\)的上界、下界、上确界、下确界.

解:

\(\{2, 3, 6\}\)的上界:6, 12, 24, 36; 上确界: 6; 下界:无; 下确界:无.

\(\{6, 12\}\)的上界:12, 24, 36; 上确界:12; 下界:2, 3, 6; 下确界:6.

例: 设\(A=\{a, b, c, d, e\}\), \(A\)上的偏序关系\(R\)的哈斯图如下.

求\(A\)的极大元、极小元、最大元、最小元、上界、下界、上确界和下确界.

解:

极大元:\(e\), 极小元:\(a\), 最大元:\(e\), 最小元:\(a\),

上界:\(e\), 下界:\(a\), 上确界:\(e\), 下确界:\(a\).

定理: 设\({\langle}A, {\leq}{\rangle}\)是偏序集, \(Q{\subseteq}A\)

若子集\(Q\)有上确界, 则上确界是唯一的.
若子集\(Q\)有下确界, 则下确界是唯一的.

从以上的论述中可以得出下面一些结论:

最大(小)元未必存在, 若存在则必唯一.
极大(小)元必存在, 但不一定唯一.

最大(小)元也必然是极大(小)元.
上(下)界未必存在, 若存在也未必唯一.
上(下)确界未必存在, 若存在则必唯一.
有上(下)确界必有上(下)界.
若\(a\)是子集\(Q\)的最大(小)元, 则\(a\)必是\(Q\)的上(下)确界; 反之, 若\(a\)是子集\(Q\)的上(下)确界且\(a{\in}Q\), 则\(a\)必是\(Q\)的最大(小)元.

定义: 设\({\langle}X, {\leq}{\rangle}\)是偏序集, 若\(X\)中任意两个元素都是可比的, 则称\({\leq}\)为全序关系, 此时称\({\langle}X, {\leq}{\rangle}\)为全序集合.

例: 在自然数集合\(N\)中的\({\leq}\)(小于等于)关系\({\langle}N, {\leq}{\rangle}\)是全序集合.

因为它是: 自反的、反对称的、传递的, 而且对任意的\(x, y{\in}N\), 必有\(x{\leq}y\)或\(y{\leq}x\)之一成立. 所以, \({\langle}N, {\leq}{\rangle}\)是全序集合.

例: 设集合\(A=\{a, b, c\}\)中, 在\(P(A)\)中定义\(\subseteq\)为集合中的包含关系, 则\(\langle P(A), \subseteq\rangle\)不是全序集合.

因为: \[P(A)=\{\Phi, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}\] 而\(\{a\}\)和\(\{b, c\}\)是不可比的, 即两者之间没有包含关系. 所以: \(\langle P(A), \subseteq\rangle\)不是全序集合.

定义: 在偏序集\({\langle}X, {\leq}{\rangle}\)中, 若\(X\)的每一个非空子集都存在最小元, 则称\({\leq}\)为良序关系, 此时称\({\langle}X, {\leq}{\rangle}\)称为良序集合.

例: 设\(Z_n=\{1, 2, 3, \cdots , n\}\), \({\leq}\)是通常的”小于等于”关系, 则\({\langle}Z_n, {\leq}{\rangle}\)是良序集, \({\langle}Z_+, {\leq}{\rangle}\)也是良序集.

但\({\langle}Z, {\leq}{\rangle}\)不是良序集, 因子集\(Z_- {\subseteq}Z\), 而\(Z_-\)中没有最小元.

定理: 良序集必是全序集.

定理: 每一个有限全序集都是良序集.