集合论

主讲教师

李辉

集合的概念

集合的定义及表示

集合的概念是数学中最基本的概念之一. 难以精确定义.

简单地说, 把一些事物汇集到一起组成一个整体称为集合(Set).

这些事物称为集合的元素(Element), 可以是具体的, 也可以是抽象的.

例: 全体中国人, 教室里的所有学习用具, 坐标平面上所有的点分别构成了三个不同的集合.

通常用大写英文字母\(A, B, C, \cdots, Z\)表示集合的名称, 用小写英文字母\(a, b, c, \cdots, z\)表示集合的元素.

集合的表示方法有两种:

枚举法

将集合的元素全部列举出来(或列出足够多的元素以反映集合的特征), 元素之间用逗号隔开, 并把它们用花括号括起来.

例:

\(A=\{a,b,c,d\}\)
\(B=\{2 ,4 ,6 ,8 ,\cdots, 2n ,\cdots \}\)
\(C=\{\{a,b\}, c, \{1,c\}\}\)
\(D=\{m_1, m_2, \cdots, m_n\}\)
\(E=\{\)电灯, 铅笔, 计算机\(\}\)

元素与集合的隶属关系:

若\(a\)是集合\(S\)中的元素, 记作\(a\in S\), 读作“\(a\)属于集合\(S\)”.
若\(a\)不是集合\(S\)中的元素, 记作\(a\notin S\), 读作“\(a\)不属于集合\(S\)”.

叙述法(描述法, 条件表示法)

将集合的元素用文字描述或谓词来概括.

\[A=\{x|P(x)\}\]

表示集合\(A\)由使\(P(x)\)为真的全体\(x\)构成.

例:

\(P=\{y|y=a \vee y=b\}\)
\(Q=\{x|x\)是素数\(\}\)
\(R=\{x|x\)是美国人\(\}\)
\(S =\{x|x\in R \wedge x^2=1\}\)
\(T=\{x|x\)是小于10的素数\(\}\)
\(U=\{x|x\)是正奇数\(\}\)

集合的性质

无序性: 一个集合中, 每个元素的地位都是相同的, 元素之间是无序的.

例: \(\{1, 2, 3, 4\}\) 和 \(\{1, 3, 2, 4\}\)是同一个集合.

确定性: 给定一个集合, 任给一个元素, 该元素或者属于或者不属于该集合, 二者必居其一.

例: 要么\(x\in S\), 要么\(x\notin S\).

互异性: 一个集合中, 任何两个元素都互不相同, 即每个元素只能出现一次.

例: \(\{1, 1, 2\}\)与\(\{1,2\}\)相同, 只有两个元素.

常常存在这样一些集合, 其元素本身也是一个集合. 例: \[X=\{a, 3, \{s,2\}, \{t\}, 8\}\]

对于这种情形, 关键是要把集合\(\{a\}\)与元素\(a\)区别开来.

在上述例子中, 集合\(\{t\}\)是集合\(X\)的元素, 即\(\{t\}\in X\).

而\(t\)是集合\(\{t\}\)的元素, 即\(t\in\{t\}\). 但\(t\)不是\(X\)的元素, 即\(t\notin X\).

特殊集合

对于一个集合\(A\), 如果它是由有限个元素组成的, 则称\(A\)为有限集合, 简称有限集; 不是有限集合的集合称为无限集合, 简称无限集.

对于一个有限集\(A\)来说, 通常把\(A\)中不同元素的个数称为\(A\)的势(基数),用\(|A|\)或\(K(A)\)来表示.

若\(A\)中包含\(m\)个不同元素, 记\(|A|=m\), 也称\(A\)为\(m\)元集.

例: \(A=\{1,2,3,a,b,c\}\), \(|A|=6\), \(A\)是6元集.

约定几个常见集合的表示符号:

\(N\): 自然数集合\(N=\{0,1,2,\cdots\}\)
\(Z\): 整数集合\(Z=\{\cdots,-2,-1,0,1,2,\cdots\}\)
\(Z_{+}\): 正整数集合\(Z_{+}=\{1,2,3,\cdots\}\)
\(Z_{-}\): 负整数集合\(Z_{-}=\{\cdots,-3,-2,-1\}\)
\(P\): 素数集合\(P=\{2,3,5,7,11,13,\cdots\}\)

\(Ev\): 偶数集合\(Ev=\{\cdots,-4,-2,0,2,4,\cdots\}\)
\(Od\): 奇数集合\(Od=\{\cdots,-3,-1,1,3,\cdots\}\)
\(R\): 实数集合
\(C\): 复数集合
\(Q\): 有理数集合

集合间的关系

几个逻辑符号的含义:

\(\vee\): 或(或者)
\(\wedge\): 与(和, 并且)
\(\rightarrow\): 如果…, 那么…(若…, 则… )
\(\Leftrightarrow\): 等价于(当且仅当)

不含任何元素的集合为空集, 记作\(\Phi\).

\[\Phi=\{x|x\neq x\}.\]

例: \(\{x|x\in R\wedge x^2+1=0\}\)是方程\[x^2+1=0\]的实数解集合, 然而该方程无实数解, 所以解集是个空集.

注意: \(\Phi\)和\(\{\Phi\}\)是不相同的集合.

\(\Phi\)是一个集合, \(\Phi\)中不含有任何元素, 而集合\(\{\Phi\}\)中含有一个元素\(\Phi\), 所以\(\Phi\in\{\Phi\}\).

设\(A,B\)是任意给定的两个集合, 如果\(A\)的每一个元素都是\(B\)的元素, 则称集合\(A\)是集合\(B\)的子集, 或称集合\(A\)包含于集合\(B\)中, 或集合\(B\)包含集合\(A\).

记作\(A\subseteq B\),或\(B\supseteq A\).

符号化: \(A\subseteq B \Leftrightarrow (x\in A \rightarrow x\in B)\)

显然,对于任意的非空集合\(S\),都有\(\Phi\subseteq S\)和\(S\subseteq S\).

称\(\Phi\)和\(S\)为\(S\)的平凡子集.

例: 设 \(A=\{1,2,3\}\), \(B=\{5,9,\{5,9\}\}\), \(C=\{1,3\}\), \(D=\{5,9\}\),

则: \(C\subseteq A\), \(D\subseteq B\).

本例中, \(D\)既是\(B\)的子集又是\(B\)的元素, 即\(D\subseteq B\)且\(D\in B\).

设\(A\), \(B\)是两个集合, 如果\(A\subseteq B\), 且\(A\neq B\), 称\(A\)是\(B\)的真子集, 记为\(A\subset B\).

例: 偶数集是整数集的真子集(\(Ev\subset Z\)), 整数集是实数集的真子集\((Z\subset R)\).

例: 设\(A=\{1, 2, 3\}\), \(B=\{1, 2\}\), \(C=\{1, 3\}\), \(D=\{3\}\),

则\(B\subset A, C\subset A, D\subset A, D\subset C\).

定理: 空集是任一集合的子集.

证明: (反证法).

设存在一个集合\(A\), \(\Phi\)不是\(A\)的子集, 则至少有一个元素\(x\), 使得\(x\in\Phi\)且\(x\notin A\).

但空集\(\Phi\)不包含任何元素, 所以假设不成立.

定理: 空集是唯一的.

证明: (反证法).

设有两个空集\(\Phi_1\)和\(\Phi_2\).

因为空集被包含于每一个集合中, 因此有\(\Phi_1\subseteq\Phi_2\)且\(\Phi_2\subseteq\Phi_1\), 于是\(\Phi_1 = \Phi_2\).

外延公理(Zermelo–Fraenkel Axiom): 如果集合\(A\)和\(B\)有完全相同的元素, 那么称集合\(A\)和\(B\)相等, 记作\(A=B\).

如果集合\(A\)与\(B\)不相等, 则记作\(A{\neq}B\).

两个集合相等可以通过两个集合相互包含来证明.

\[A=B{\Leftrightarrow}A{\subseteq}B{\wedge} B{\subseteq}A\]

例: 设\(A=\{3, 6, 9\}\), \(B=\{6, 3, 9\}\), \(C=\{3, \{6\}, 9\}\), 则: \(A=B\), \(A{\neq}C\).

对于任意集合\(A\), \(B\)和\(C\), 有

\(A{\subseteq}A\). \(\subseteq\)具有自反性(Reflexivity).
\(A{\subseteq}B\)且\(B{\subseteq}A\),则\(A=B\). \(\subseteq\)具有反对称性(Antisymmetric).
\(A{\subseteq}B\)且\(B{\subseteq}C\),则\(A{\subseteq}C\).\(\subseteq\)具有传递性(Transitivity)

给定集合\(A\), 以\(A\)的全部子集为元素构成的集合, 称为\(A\)的幂集(Power set), 记为\(P(A)\)或\(2^A\). 即: \(P(A)=\{x|x{\subseteq}A\}\)

例: 设\(A=\{1,2,3\}\), \(B=\{a,b\}\), \(C=\{\Phi\}\), 求\(A\), \(B\)和\(C\)的幂集.

解:

\(P(A)=\{\Phi, \{1\}, \{2\}, \{3\},\{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}\}\)

\(P(B)=\{\Phi, \{a\}, \{b\}, \{a,b\} \}\)

\(P(C)=\{\Phi, \{\Phi\}\}\)

空集\(\Phi\)的幂集: \(P(\Phi)=\{\Phi\}\).

定理: 如果有限集合\(A\)有\(n\)个元素, 则它的幂集\(P(A)\)有\(2^n\)个元素.

证明: 从集合\(A\)中:

任意抽取0个元素构成的子集共有个\(C_n^0\)

任意抽取一个元素构成的子集共有个\(C_n^1\)

任意抽取两个元素构成的子集共有个\(C_n^2\)

\(\cdots\cdots\)

任意抽取n个元素构成的子集共有个\(C_n^n\)

\(C_n^0+C_n^1+C_n^2+\cdots+C_n^n=2^n\)

若一个集合\(A\)的所有元素都是集合, 称该集合为集合族. 幂集就是一个集合族.

\(A=\{ \{1,2\}, \{a\}, \{\)张三,老虎,10\(\} \}\)是集合族.

给定一个集合, 如果讨论范围内的所有集合都是它的子集, 称该集合为全集(Universal Set). 记作\(U\).

全集是一个相对的概念, 由于研究的问题不同, 所取的全集也不同.

例: 在研究平面上直线的关系时, 可以把整个平面上的点坐标作为全集.

例: 在研究有关整数问题时, 可以取整数集合\(Z\)作为全集, 也可以取有理数集合\(Q\)作为全集, 还可以取实数集合\(R\)作为全集.

一般情况下, 全集应尽量取小一些. 这样的话, 问题的描述和处理相对容易.

设\(A\), \(B\)是任意给定的两个集合, \(A\)和\(B\)的交集\(A\cap B\), 并集\(A\cup B\) , \(B\)对\(A\)的相对补集\(A-B\), 以及对称差集\(A\bigoplus B\) 分别定义如下:

\(A\cap B=\{x|x\in A\wedge x\in B\}\)
\(A\cup B=\{x|x\in A\vee x\in B\}\)
\(A-B=\{x|x\in A\wedge x\notin B\}\)
\(A\bigoplus B=(A-B)\cup (B-A)=\{x|(x\in A\wedge x \notin B)\vee (x\in B\wedge x \notin A\}\)

设\(A=\{a,b,c,d\}\),\(B= \{e,f,a,d\}\), 求: \(A\cap B\), \(A\cup B\), \(A-B\), \(A\bigoplus B\).

解: \(A\cap B=\{a,d\}\), \(A\cup B=\{a,b,c,d,e,f\}\), \(A-B=\{b,c\}\), \(B-A=\{e,f\}\), \(A\bigoplus B= \{ b,c,e,f\}\)

定义:设\(U\)是全集,\(A\)是\(U\)的任一子集,\(U-A\)称为集合\(A\)的绝对补集. 记作\(\sim A\)或\(A^c\).

\(\sim A=U- A= \{ x|x\in U\wedge x\notin A\}\)

由集合\(A\)的绝对补集可知: 若\(x{\notin}A\), 则\(x\in{\sim}A\); 若\(x{\in}A\), 则\(x\notin{\sim}A\).

例: 设\(U=\{0, 1, 2, 3\}\), \(A=\{1, 2, 3\}\), \(B=\{0, 1, 2, 3\}\), \(C=\Phi\), 求\(\sim A, \sim B, \sim C\).

解: \[\sim A=\{0\},\,\,\sim B=\Phi,\,\,\sim C=\{0,1,2,3\}.\]

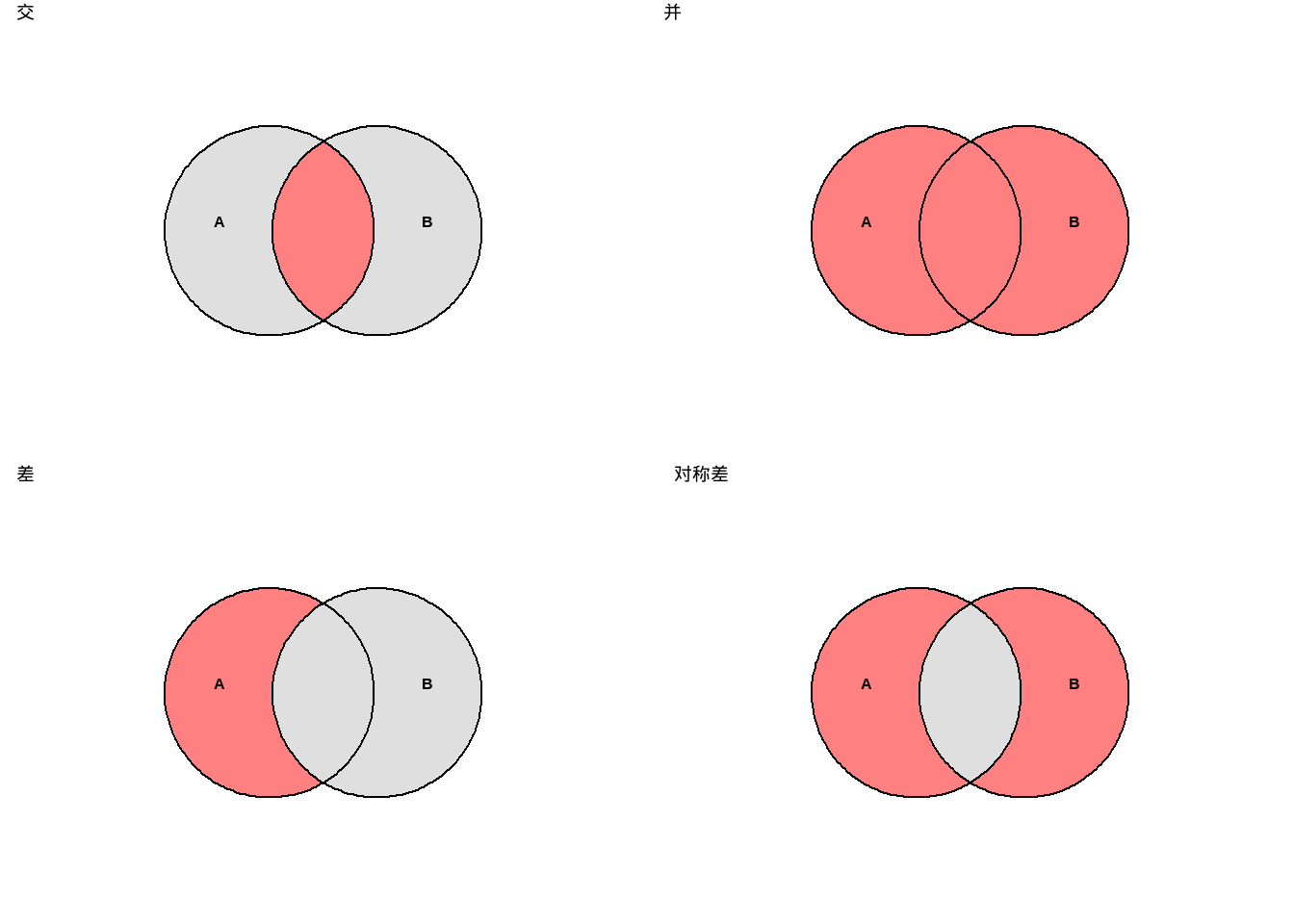
维恩图

当集合中的元素不多时, 可以用维恩图(Venn diagram)或文氏图直观地表示集合间的关系及运算结果.

在维恩图中, 通常用一个矩形表示全集\(U\). 然后在矩形的内部画一些圆(或其它封闭的曲线), 圆的内部代表集合, 不同的圆代表不同的集合.

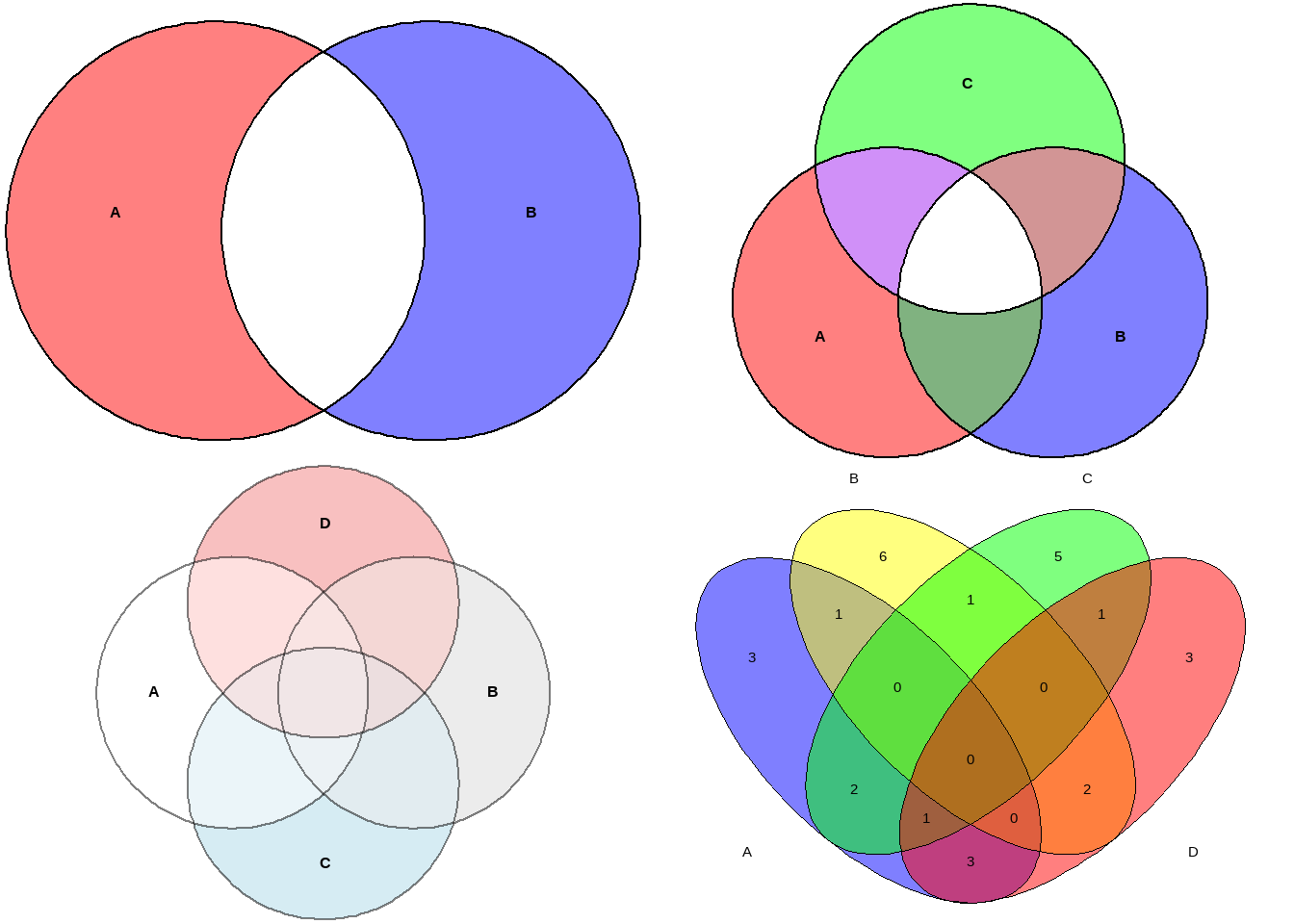
2、3、4个集合对应的维恩图

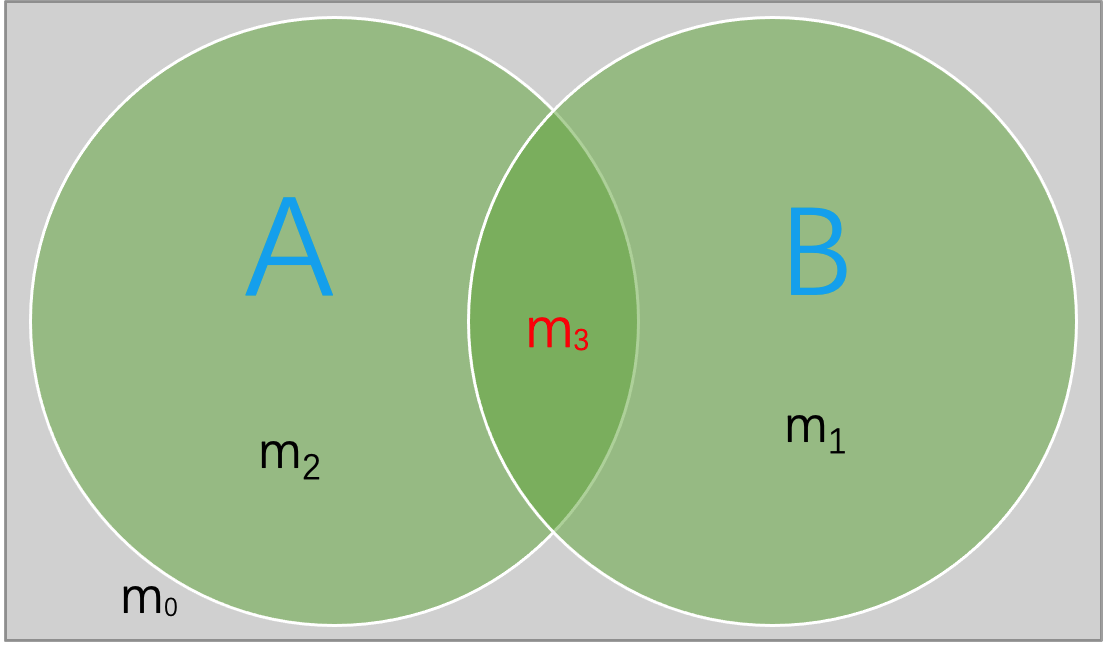
集合\(A\), \(B\)将全集\(U\)划分成4个子集\(m_0\), \(m_1\), \(m_2\), \(m_3\),称为极小项.

\[A{\cap}B = m_3\] \[A{\cup}B = m_1{\cup}m_2{\cup}m_3\]

\[A-B=m_2\] \[B-A = m_1\]

\[A{\oplus}B = m_1{\cup}m_2\]

\[{\sim}A= m_0{\cup}m_1\]

\[{\sim}B=m_0{\cup}m_2\]

任意两个极小项交集为空, 因此 \[m_i\cup m_j = m_i\oplus m_j\]

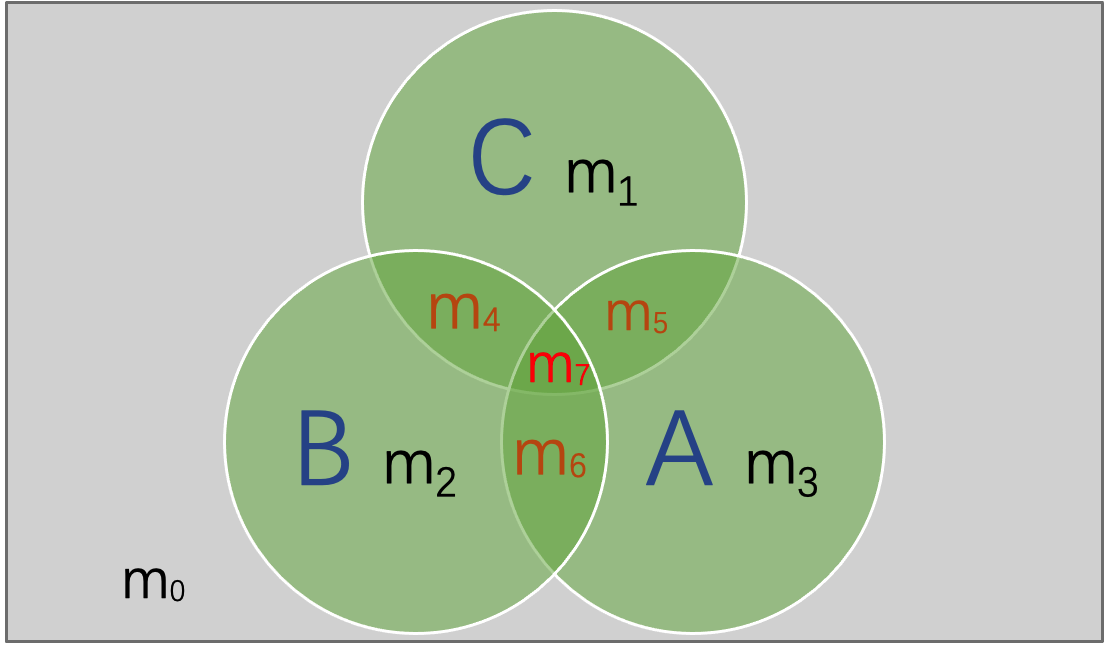
设\(A\), \(B\)是任意的集合, 运用下面的规则可以产生集合公式.

集合\(A\)是集合公式.
若\(A\)是集合公式, 则\({\sim}A\)也是集合公式.
若\(A,B\)是集合公式, 则\((A{\cup}B)\), \((A{\cap}B)\), \((A-B)\), \((A{\oplus}B)\)也都是集合公式.
有限次地使用以上规则得到的公式都是集合公式.

为减少使用括号的数量, 有时候省略集合公式的最外层括号.

例: \[(A{\cup}B){\cap}C, \,\, (A{\oplus}B){\cap}(B-C), \,\, (B{\oplus}D)\oplus((B-C)-D)\]

都是集合公式.

集合恒等式

一些基本集合恒等式(集合定律), 其中\(A,B,C\)是全集\(U\)的任意子集.

幂等律(Idempotent Laws)

\[A\cup A=A, \, A\cap A=A\]

交换律(Commutative Property)

\[A\cup B=B\cup A\]

\[A\cap B=B\cap A\]

\[A\oplus B=B\oplus A\]

结合律(Associative Property)

\[(A\cup B)\cup C=A\cup(B\cup C)\]

\[(A\cap B)\cap C=A\cap(B\cap C)\]

\[(A\oplus B)\oplus C=A\oplus(B\oplus C)\]

分配律(Distributive Property)

\[A\cup(B\cap C) = (A\cup B)\cap(A\cup C)\]

\[A\cap(B\cup C) = (A\cap B)\cup(A\cap C)\]

\[A\cap(B-C)=(A\cap B)-(A\cap C)\] 注意:

\[A\cup(B-C)\neq(A\cup B)-(A\cup C)\]

\[A\cup(B-C)=(A\cup B)-(C-A)\]

同一律(Identity)

\[A\cup\Phi=A, \, A\cap U=A\]

\[A-\Phi=A, \, A\oplus\Phi=A\]

零律或支配律(Domination Laws)

\[A\cup U=U, \, A\cap\Phi=\Phi\]

互补律(Complement)

\[A\cup\sim A=U, \, A\cap\sim A=\Phi\]

\[\sim U=\Phi, \, \sim\Phi=U\]

吸收律(Absorption Laws)

\[A\cup(A\cap B)=A\] \[A\cap(A\cup B)=A\]

德·摩根律(De Morgan’s Laws)

\[\sim(A\cup B)=\sim A\cap\sim B\]

\[\sim(A\cap B)=\sim A\cup\sim B\]

\[A-(B\cup C)=(A-B)\cap(A-C)\]

\[A-(B\cap C)=(A-B)\cup(A-C)\]

双重否定律(Double Complement)

\[\sim(\sim A)=A\]

\(A\oplus A=\Phi, \, A-A=\Phi\)
\(A\cap B\subseteq A, \, A\cap B\subseteq B\)
\(A\subseteq A\cup B,\, B\subseteq A\cup B\)
\(A-B\subseteq A,\, A-B=A\cap\sim B\)
\(A\oplus B=(A-B)\cup(B-A)=(A\cup B)-(A\cap B)=(A\cap\sim B)\cup(\sim A\cap B)\)

由于集合的交, 并运算满足结合律, 当多个集合进行交运算或并运算时, 可以写成:

\[S_1\cap S_2\cap \cdots \cap S_n=\bigcap_{i=1}^n{S_i}\]

\[S_1\cup S_2\cup \cdots \cup S_n=\bigcup_{i=1}^n{S_i}\]

设 \[S_1=\{3,c\},\,\, S_2=\{a,c\},\,\,S_3=\{c,2\},\,\, S_4=\{c,3\}\]

那么 \[\bigcap_{i=1}^4{S_i}=\{c\}\] \[\bigcup_{i=1}^4{S_i}=\{a,c,2,3\}\]

以上集合恒等式, 可以采用三种方式证明:

基本定义法
维恩图法
公式推演法

例: 设\(A\), \(B\)为任意两个集合, 则\(A-B=A\cap{\sim}B\).

证明(基本定义法): 拟证明\(A-B\)和\(A\cap{\sim}B\)相互包含.

对于任意的\(x\), 若\(x{\in}A-B\), 则\(x{\in}A\wedge x{\notin}B\), 即\(x{\in}A{\wedge}x\in{\sim}B\), 于是\(x{\in}A\cap{\sim}B\).

所以\(A-B\subseteq A\cap\sim B\).

反之, 对于任意的\(x\), 若\(x{\in}A\cap{\sim}B\), 则\(x{\in}A{\wedge}x\in{\sim}B\), 即\(x{\in}A{\wedge}x{\notin}B\).

所以\(x{\in}A-B\), 故\(A\cap{\sim}B{\subseteq}A-B\).

综上, \(A-B=A\cap{\sim}B\).证毕.

(维恩图法)

\[A=m_2\cup m_3\]

\[\sim B=m_0\cup m_2\]

\[ A\cap\sim B= m_2\]

\[ A-B = m_2\]

所以 \(A-B=A\cap\sim B\).

证明结合律 \[(A\cap B)\cap C=A\cap (B\cap C).\]

证明(基本定义法).

对于任意的\(x\),若\(x\in(A\cap B)\cap C\), 则 \[x\in (A\cap B)\wedge (x\in C),\] \[(x\in A\wedge x\in B)\wedge (x\in C),\] \[x\in A\wedge (x\in B\wedge x\in C),\] \[x\in A\wedge x\in (B\cap C),\] \[x\in A\cap (B\cap C),\] \[(A\cap B)\cap C \subseteq A\cap (B\cap C)\]

反之, 对于任意的\(x\), 若\(x\in A\cap (B\cap C)\), 则 \[x\in A\wedge x\in (B\cap C),\] \[x\in A\wedge (x\in B\wedge x\in C),\] \[(x\in A\wedge x\in B)\wedge (x\in C),\] \[x\in (A\cap B)\wedge (x\in C),\] \[x\in (A\cap B)\cap C,\] \[A\cap (B\cap C)\subseteq(A\cap B)\cap C\] 因此\[(A\cap B)\cap C=A\cap (B\cap C)\]

证明: \((A\cap B)\cap C=A\cap (B\cap C).\)

(维恩图法)

\[A= m_3\cup m_5\cup m_6\cup m_7\] \[C= m_1\cup m_4\cup m_5\cup m_7\] \[A\cap B = m_6\cup m_7,\] \[B\cap C= m_4\cup m_7\] \[(A\cap B)\cap C= (m_6\cup m_7 )\cap (m_1\cup m_4\cup m_5\cup m_7 )= m_7\] \[A\cap (B\cap C)=(m_3\cup m_5\cup m_6\cup m_7 )\cap (m_4\cup m_7 ) = m_7\] \[\therefore\,\,(A\cap B)\cap C=A\cap (B\cap C)\]

设\(A\subseteq B,C\)是任意集合, 求证: \[A\cap C\subseteq B\cap C.\]

证明: 由\(A\subseteq B\)知, 若\(x\in A\), 则\(x\in B\).

若\(x\in A\cap C\), 有\(x\in A\wedge x\in C\), 则

\[x\in B \wedge x\in C.\] \[x\in B\cap C.\] 因此 \(A\cap C\subseteq B\cap C.\)

设\(A\subseteq B\), \(C\subseteq D\), 求证: \[A\cup C\subseteq B\cup D.\]

证明: 任取\(x\in A\cup C\), 由“并”运算的定义有:

\(x\in A\) 或 \(x\in C.\)

若\(x\in A\), 则由\(A\subseteq B\), 有\(x\in B\), 故\(x\in B\cup D\)

若\(x\in C\), 则由\(C\subseteq D\), 有\(x\in D\), 故\(x\in B\cup D\).

因此 \(A\cup C\subseteq B\cup D.\)

求证: \(A\subseteq B\) 当且仅当 \(A\cup B = B.\)

证明:

(必要性) 设\(A\subseteq B\),则\(x\in A\),必有\(x\in B\).

若\(x\in A\cup B\), 有\(x\in A\)或\(x\in B\).

一定有\(x\in B\), 所以\(A\cup B\subseteq B\).

又因为\(B\subseteq A\cup B\), 于是\(A\cup B=B\).

(充分性)若\(A\cup B=B\), 因为\(A\subseteq A\cup B\), 所以\(A\subseteq B\).

用公式推演法也可以证明集合恒等式.

证明分配律: \(A\cap (B-C)=(A\cap B)-(A\cap C)\).

证明: \(A\cap (B-C)=A\cap (B\cap \sim C)=A\cap B\cap \sim C\)

又\[\begin{gather} (A\cap B)-(A\cap C)\\ =(A\cap B)\cap \sim (A\cap C)\\ =(A\cap B)\cap (\sim A\cup \sim C)\\ =(A\cap B\cap \sim A)\cup (A\cap B\cap \sim C)\\ =\Phi\cup (A\cap B\cap \sim C)\\ =A\cap B\cap \sim C\\ \end{gather}\] 因此 \(A\cap (B-C)=(A\cap B)-(A\cap C).\)

证明吸收律: \(A\cup (A\cap B)=A.\)

证明: \[\begin{gather} A\cup (A\cap B)\\ =(A\cap U)\cup (A\cap B)\\ =A\cap (U\cup B)\\ =A\cap U\\ =A \end{gather}\]

证明分配律: \(A\cap (B\cup C)=(A\cap B)\cup (A\cap C).\)

证明: \[\begin{gather} x\in A\cap (B\cup C)\\ \Leftrightarrow x\in A\wedge x\in (B\cup C)\\ \Leftrightarrow x\in A\wedge (x\in B\vee x\in C)\\ \Leftrightarrow (x\in A\wedge x\in B)\vee (x\in A\wedge x\in C)\\ \Leftrightarrow (x\in A\cap B)\vee (x\in A\cap C)\\ \Leftrightarrow x\in (A\cap B)\cup (A\cap C) \end{gather}\] 所以 \(A\cap (B\cup C)=(A\cap B)\cup (A\cap C).\)

证明交换律: \(A\cap B=B\cap A.\)

证明: \[\begin{gather} x\in A\cap B\\ \Leftrightarrow x\in A\wedge x\in B\\ \Leftrightarrow x\in B\wedge x\in A\\ \Leftrightarrow x\in B\cap A \end{gather}\] 所以 \(A\cap B=B\cap A.\)

证明结合律: \((A\cap B)\cap C=A\cap (B\cap C).\)

证明: \[\begin{gather} x\in (A\cap B)\cap C\\ \Leftrightarrow x\in (A\cap B)\wedge (x\in C)\\ \Leftrightarrow (x\in A\wedge x\in B)\wedge (x\in C)\\ \Leftrightarrow (x\in A)\wedge (x\in B\wedge x\in C)\\ \Leftrightarrow (x\in A)\wedge x\in (B\cap C)\\ \Leftrightarrow x\in A\cap (B\cap C) \end{gather}\]

所以\((A\cap B)\cap C=A\cap (B\cap C).\)

同理可证\((A\cup B)\cup C=A\cup (B\cup C).\)

证明幂等律: \(A\cup A=A.\)

证明: \[\begin{gather} x\in A\cup A\\ \Leftrightarrow x\in A\vee x\in A\\ \Leftrightarrow x\in A \end{gather}\] 所以\[A\cup A=A.\]

证明德·摩根定律: \(\sim (A\cup B)=\sim A\cap \sim B.\)

证明: \[\begin{gather} \sim (A\cup B)=\{x|x\in \sim (A\cup B)\}\\ =\{x|x\notin(A\cup B)\}\\ =\{x|(x\notin A)\wedge (x\notin B)\}\\ =\{x|(x\in \sim A)\wedge (x\in \sim B)\}\\ =\sim A\cap \sim B \end{gather}\]

设\(A\), \(B\)为任意两个集合, 若\(A\subseteq B\), 则:

\(\sim B\subseteq \sim A\), \((B-A)\cup A=B\)

证明:

若\(x\in A\), 则\(x\in B.\)

因此, \(x\notin B\) 必有 \(x\notin A\).

故 \(x\in \sim B\) 必有 \(x\in \sim A\).

即 \(\sim B\subseteq \sim A.\)

\[\begin{gather} (B-A)\cup A\\ =(B\cap \sim A)\cup A\\ =(B\cup A)\cap (\sim A\cup A)\\ =(B\cup A)\cap U\\ =B\cup A \end{gather}\] 因为 \(A\subseteq B\), 于是有 \(B\cup A=B\).

因此 \[(B-A)\cup A=B.\]

基本计数原理

计数是在数学中经常遇到的问题. 许多组合问题都涉及到计数, 有时候需要考虑的对象往往很多, 于是希望能对一个集合中的对象进行计数, 而不是把它们全部列举出来.

本节介绍两个基本的计数原理: 加法原理和乘法原理.

定理(加法原理): 假设有\(k\)个集合, 其中第1个集合有\(n_1\)个元素, 第2个集合有\(n_2\)个元素, 依此类推.

如果所有的元素都不相同(即\(k\)个集合两两互不相交), 那么可以从这些集合选出的元素总数为: \[n_1+ n_2+\cdots + n_k\]

例: 1个学生可以从3类选修课中选修1门课程, 这3类选修课分别包含5, 11和9门选修课, 那么该学生有多少种选修方式？

解: 该学生对第1类课程的选修有5种方式, 第2类课程的选修有11种方式, 第3类课程的选修有9种方式. 因此, 共有5+11+9=25种选修课程方式.

加法原理是说: 整体等于其部分之和.

例: 1-100之间(包括1和100)共有多少个整数是偶数或以5结尾？

证明: 用\(A\)代表1-100之间的偶数集合, \(B\)代表1-100之间以5结尾的整数的集合, 且\(A\)和\(B\)中的元素是不相同的, 则\(A\cup B\)就是1-100之间的偶数和以5结尾的整数集合.

可见\(A\)包含50个元素, \(B\)包含10个元素, 因此1-100之间的偶数或以5结尾的整数共有50+10=60.

定理(乘法原理): 假定一个任务需要\(k\)步完成. 如果执行第一步的方法有\(n_1\)种, 执行第二步的方法有\(n_2\)种, 执行第\(i\)步(\(i=3,4,\cdots,k\))有\(n_i\)种方法.

那么执行整个任务的不同方法就有: \[n_1 n_2\cdots n_k.\]

例: 设一标识符由2个字符组成, 第1个字符为\(a,b,c,d,e\)中的一个字母, 第2个字符1,2,3中的一个数字, 问共可以组成多少不同的标识符？

证明: 第一步为从\(a,b,c,d,e\)中选择1个字符作为标识符的第1个字符, 共有5种方式. 第二个步为从1,2,3中选择1个字符作为标识符的第2个字符, 共有3种方式. 根据乘法原理有5×3=15种不同的标识符.

求证: 含有\(n\)个元素的集合共有\(2^n\)个子集.

证明: 设该集合为\(X=\{x_1,x_2,\cdots x_n\}\).

构造的一个子集可分为\(n\)个步骤:选取或不选取\(x_1\), 选取或不选取\(x_2\), \(\cdots\),选取或不选取\(x_n\). 每一步骤有2种选择, 故所有可能的子集总数为: \[2\times 2\times\cdots\times 2\times 2=2^n.\]

计数问题不仅可以使用乘法原理或加法原理来解决, 也可以同时使用这两个原理来解决.

例: 设\(A,B,C\)是3个城市, 从\(A\)到\(B\)有3条路, 从\(B\)到\(C\)有4条路, 从\(A\)到\(C\)有5条路, 问从\(A\)到\(C\)有多少种不同的方式?

解: \[3\times 4+5=17.\]

容斥原理

设\(A_1,A_2\)为有限集合,显然下列各式成立:

\(|A_1\cup A_2|\leq |A_1|+|A_2|\)

\(|A_1\cap A_2|\leq min(|A_1|,|A_2|)\)

\(|A_1-A_2|\ge |A_1|-|A_2|\)

\(|A_1\oplus A_2|=|A_1|+|A_2|-2|A_1\cap A_2|\)

\(|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|\)

这些公式可由维恩图得出.

最后一个公式称为容斥原理. 容斥原理研究若干有限集合交与并的计数问题.

例: 在10个青年人中有5个是北京人, 7个是学生, 其中既是北京人又是学生的青年有3人, 问不是北京人又不是学生的青年有几人？

解: 设U:青年人集合, A:学生集合, B:北京人集合. |U|=10,|A|=7,|B|=5, 则:

\(A\cup B\): 北京人或学生组成的集合.

\(\sim (A\cup B)\): 不是北京人也不是学生组成的集合.

\(A\cap B\): 是北京人又是学生组成的集合. \(|A\cap B|=3\).

则\(|A\cup B|=|A|+|B|-|A\cap B|=7+5-3=9\).

故\(|\sim (A\cup B)|=|U|-| A\cup B |=10-9=1\).

即: 既不是北京人又不是学生的青年人有1人.

容斥原理可以推广到多个集合.

设\(A,B,C\)为有限集合,有: \[|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B \cap C|.\] 定理: 设\(A_1,A_2,A_3,\cdots,A_n\)为有限集, 则 \[\biggl|\bigcup_{i=1}^n A_i\biggr| = \sum_{i=1}^n\left|A_i\right|\; -\sum_{1 \le i < j \le n}\left|A_i\cap A_j\right|\; + \sum_{1 \le i < j < k \le n}\left|A_i\cap A_j\cap A_k\right|\;-\ \cdots\ +\; \left(-1\right)^{n-1} \left|A_1\cap\cdots\cap A_n\right|.\]

例: 设某高校足球队有球员38人, 篮球队有球员15人, 棒球队有球员20人, 三队队员总数为58人, 且其中只有3人同时参加三个队, 试求同时参加两个队的队员共有几人？

解: 设\(A\): 足球队员集合, \(B\): 篮球队员集合, \(C\): 棒球队员集合. \(|A|=38\),\(|B|=15\), \(|C|=20\), \(|A\cup B\cup C|=58\), \(|A\cap B\cap C|=3\) \[|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B \cap C|\]

\[58=38+15+20-(|A\cap B|+|A\cap C|+|B\cap C|)+3\] \[|A\cap B|+|A\cap C|+|B\cap C|=73+3-58=18\] 由于: \(|A\cap B\cap C|=3=|m_7|\) \[|A\cap B|=|m_6|+|m_7|,|A\cap C|=|m_5|+|m_7|,|B\cap C|=|m_4|+|m_7|\] \[|A\cap B|+|A\cap C|+|B\cap C|=|m_6|+|m_5|+|m_4|+3\times|m_7|\]

同时参加两个队的队员人数是\(|m_6|+|m_5|+|m_4|+|m_7|=18-3-3=12\)人.

鸽巢原理

鸽巢原理(抽屉原理), 是离散数学中的一个重要原理. 以德国著名数学家狄利克雷(Peter Gustav Lejeune Dirichlet, 1805-1855)命名，常被称作狄利克雷原理(Dirichlet’s drawer principle). 鸽巢原理主要用于证明某些存在性或必然性的问题, 在数论、组合论以及集合论等领域中有广泛应用。

一群鸽子飞回鸽巢中,如果鸽子的数目比鸽巢多, 那么一定至少有一个鸽巢里有2只或2只以上的鸽子, 这就是鸽巢原理.

定理(鸽巢原理): 如果\(n+1\)(\(n\)为正整数)个或更多的对象被放入\(n\)个抽屉中, 则至少有一个放入2个或更多的对象.

证明: 假设\(n\)个抽屉中没有一个抽屉中有多于1个的对象, 那么对象总数至多是\(n\), 这与至少有\(n+1\)个对象相矛盾.

例: 至少要从集合\(S = \{1,2,3,4,5,6,7,8,9\}\) 中取出几个元素能保证有两个数相加等于10？

解: 将1-9分成5个不同的集合(鸽巢):

{1,9},{2,8},{3,7},{4,6},{5}

由鸽巢原理, 任取\(S\)中的6个数, 一定会有两个数(对象)在1个集合(鸽巢)中, 相加等于10.

例: 任意8个正整数每个用7来除, 其中至少有两个余数相同, 请说明理由.

解: 因为任意正整数除以7的余数最多只有0到6, 一共7种可能.

所以, 任意8个正整数, 每个都用7来除, 把余数为0的放到0号抽屉, 把余数为1的放到1号抽屉, 把余数为6的放到6号抽屉, \(\cdots\cdots\).有8个数, 被放到7个抽屉里, 至少有1个抽屉中有2个数, 即这2个数除以7的余数相同.

广义抽屉原理

定理(广义抽屉原理): 如果\(n\)个抽屉被\(kn+1\)个或更多的对象占据(\(n,k\)为正整数), 则至少有一个抽屉有\(k+1\)个或更多的对象.

证明(反证法): 假设没有抽屉中装有比\(k\)个对象多的鸽巢屉, 则对象的总数至多是\(kn\)个, \(kn<kn+1\), 这与存在有不少于\(kn+1\)对象相矛盾.

广义抽屉原理也可描述为: 如果\(m\)个对象放到\(n\)个抽屉中, 那么至少有1个抽屉有至少\(\lceil m/n \rceil\)对象.

一类普通的问题是: 把\(m\)个对象分到\(n\)个抽屉中要使得某个抽屉至少有\(r\)个对象, 求\(m\)的最小值.

例: 求1个班的同学中能保证3人在同一月份出生的最少学生数量.

解: 此处\(n=12\)个月份为鸽巢, 而\(k+1=3\), 即\(k=2\). 因此, \(kn+1=25\)个同学中, 有3人在同一月份出生.

例: 从一幅标准52张扑克牌中必须选多少张牌才能保证选出的牌中至少有3张是同样花色的？

解: 假设存在四个抽屉(n=4)存放四种花色的牌, 选中的牌放在同样花色的抽屉中. 根据广义抽屉原理,如果选了m张牌, 那么至少有一个抽屉放入至少\(\lceil m/4 \rceil\)张牌.

因此如果\(\lceil m/4 \rceil\ge 3\), 则至少选了3张同样花色的牌. 使得\(\lceil m/4 \rceil\ge 3\)的最小正整数\(m\)是\(m=2×4+1=9\).

所以选择9张牌就可以保证至少有3张是同样花色的.

例: 在\(n+1\)个小于等于\(2n\)的不相等的正整数中, 一定存在两个数是互素的.

证明: 先证下面事实:任意两个相邻的正整数是互素的.

反证法. 假设\(n\)与\(n+1\)有公因子\(q(q\ge 2)\), 则有 \(n=qp_1,n+1=qp_2\), 即\(q(p_2-p_1)=1\),这与\(q\ge 2\)和\(p_2-p_1\)是整数相矛盾. 因此,任意两个相邻的正整数是互素的.

现把\(1,2,3,\cdots,2n\)分成如下分组:

\(\{1,2\},\{3,4\},\cdots,\{2n-1,2n\}\)

从组中任取\(n+1\)个数, 根据鸽巢原理至少有两个数取自同一个鸽巢, 它们是相邻的数, 必互素.