Comp520MLCourse-8.4-Recursion

递归

阶乘运算


xxxxxxxxxx
10
1
factorial(0,1).
2
  
3
factorial(A,B) :-  
4
           A > 0, 
5
           C is A-1,
6
           factorial(C,D),
7
           B is A*D. 
8

9
?- factorial(10,What).
10
What = 3628800.

实现外取操作


xxxxxxxxxx
18
1
takeout(A,[A|B],B).
2
takeout(A,[B|C],[B|D]) :-
3
          takeout(A,C,D).
4

5
?- takeout(X,[1,2,3,4],Y).
6
X = 1,
7
Y = [2, 3, 4] ;
8
X = 2,
9
Y = [1, 3, 4] ;
10
X = 3,
11
Y = [1, 2, 4] ;
12
X = 4,
13
Y = [1, 2, 3] ;
14
false.
15

16
?- takeout(X,[1,2,3,4],_), X>3.
17
X = 4 ;
18
false.

实现汉诺塔


xxxxxxxxxx
31
1
move(1,X,Y,_) :-  
2
  write('Move top disk from '), 
3
  write(X), 
4
  write(' to '), 
5
  write(Y), 
6
  nl. 
7
move(N,X,Y,Z) :- 
8
  N>1, 
9
  M is N-1, 
10
  move(M,X,Z,Y), 
11
  move(1,X,Y,_), 
12
  move(M,Z,Y,X).
13

14
?- move(4,left,right,center).
15
Move top disk from left to center
16
Move top disk from left to right
17
Move top disk from center to right
18
Move top disk from left to center
19
Move top disk from right to left
20
Move top disk from right to center
21
Move top disk from left to center
22
Move top disk from left to right
23
Move top disk from center to right
24
Move top disk from center to left
25
Move top disk from right to left
26
Move top disk from center to right
27
Move top disk from left to center
28
Move top disk from left to right
29
Move top disk from center to right
30
true ;
31
false.


xxxxxxxxxx
10
1
edgelist02 <- c(1,2,1,3,1,4,2,5,2,6,3,7,7,11,7,12,4,8,4,9,4,10)
2
ne <- length(edgelist02)/2
3
nv <- max(edgelist02)
4
g02 <- graph(edgelist02,directed=T)
5
g02 <- set_vertex_attr(g02, "label", value = letters[1:nv])
6
g02 <- set_vertex_attr(g02, "label.degree", value = c(-pi/2,rep(0,nv-1)))
7
g02 <- set_vertex_attr(g02, "label.dist", value = rep(2,nv))
8
g02 <- set_vertex_attr(g02, "label.cex", value = rep(1.2, nv))
9
g02 <- set_edge_attr(g02, "color", value = rep("#006400",ne))
10
plot(g02,layout=layout_as_tree)

实现树结构

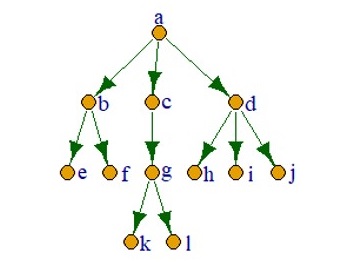
定义几个操作符


xxxxxxxxxx
4
1
:- op(500,xfx,'is_parent').
2
:- op(500,xfx,'is_sibling_of').
3
:- op(500,xfx,'is_same_level_as').
4
:- op(500,xfx,'has_depth').

创建tree数据库


xxxxxxxxxx
5
1
a is_parent b. a is_parent c. a is_parent d.
2
b is_parent e. b is_parent f.
3
c is_parent g. 
4
d is_parent h. d is_parent i. d is_parent j.
5
g is_parent k. g is_parent l.

定义"is_sibling_of"


xxxxxxxxxx
3
1
X is_sibling_of Y :- Z is_parent X,
2
  Z is_parent Y,
3
  X \== Y.

定义"is_same_level_as"


xxxxxxxxxx
4
1
X is_same_level_as X .    
2
X is_same_level_as Y :- W is_parent X,
3
  Z is_parent Y,
4
  W is_same_level_as Z.

定义"has_depth"，这里用到了cut技术，即"!"，将在后面介绍。


xxxxxxxxxx
5
1
a has_depth 0 :- !. 
2
Node has_depth D :-
3
  Mother is_parent Node,
4
  Mother has_depth Dp,
5
  D is Dp + 1.

定义"path"(path是一条从根到该节点的路径)


xxxxxxxxxx
9
1
path(Node) :-
2
  parent_path(Node),
3
  write(Node).
4
parent_path(a).
5
parent_path(Node) :-
6
  Mother is_parent Node,
7
  parent_path(Mother),
8
  write(Mother),
9
  write(' --> ').

定义“height” (height是从该节点到其下某个叶子的最大路径长度)


xxxxxxxxxx
6
1
height(N,H) :- setof(Z,ht(N,Z),Set),
2
    max(Set,0,H).
3
ht(Node,0) :- leaf(Node), !.
4
ht(Node,Hn) :- Node is_parent Child,
5
    ht(Child,Hc),
6
    Hn is Hc+1.

setof是一个内置谓词(参见Predicate setof/3), 搜集各个分支的高度汇总到Set变量中。

定义"leaf"(叶子节点)


xxxxxxxxxx
1
1
leaf(Node) :- not(Node is_parent Child).

定义"max"


xxxxxxxxxx
3
1
max([],M,M).
2
max([X|R],M,A) :-
3
  (X > M -> max(R,X,A) ; max(R,M,A)).

目标


xxxxxxxxxx
42
1
?- max([3,9,8],7,X).
2
X = 9.
3

4
?- max([3,9,11,8],14,X).
5
X = 14.
6

7
?- leaf(f).
8
true.
9

10
?- leaf(g).
11
false.
12

13
?- X is_sibling_of i.
14
X = h ;
15
X = j ;
16
false.
17

18
?- X is_same_level_as c.
19
X = c ;
20
X = b ;
21
X = c ;
22
X = d ;
23
false.
24

25
?- k has_depth X.
26
X = 3.
27

28
?- parent_path(k).
29
a --> c --> g --> 
30
true ;
31
false.
32

33
?- path(k).
34
a --> c --> g --> k
35
true ;
36
false.
37

38
?- height(c,X).
39
X = 2.
40

41
?- height(k,X).
42
X = 0.