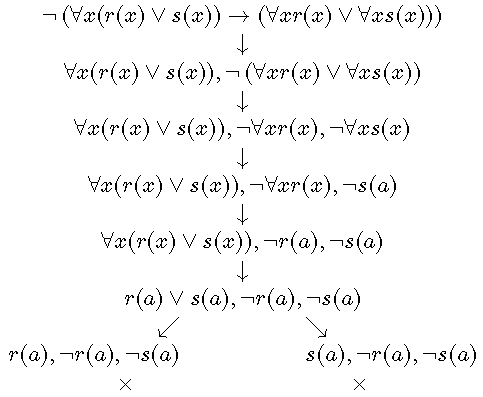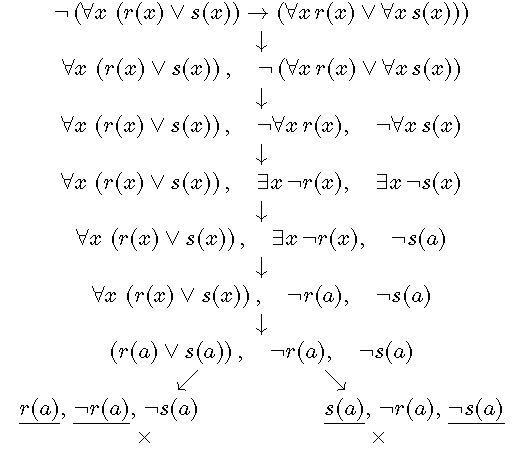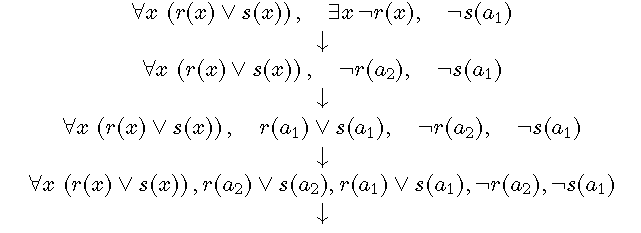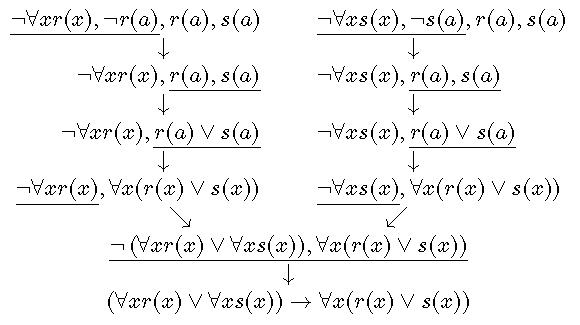一阶逻辑推导

正确的语义树：

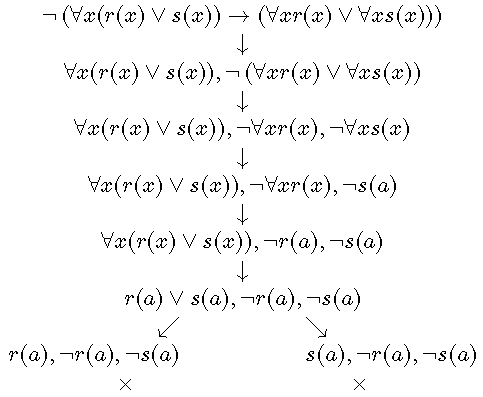
错误的语义树：

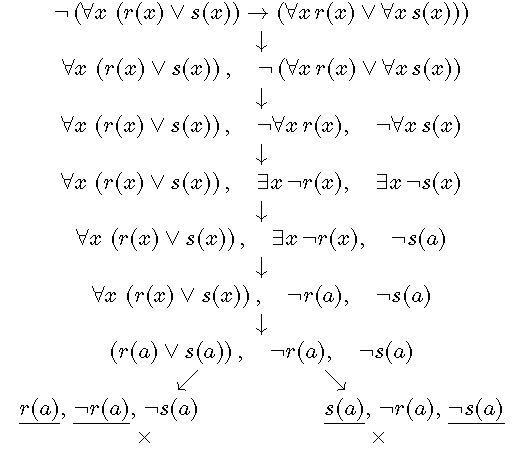
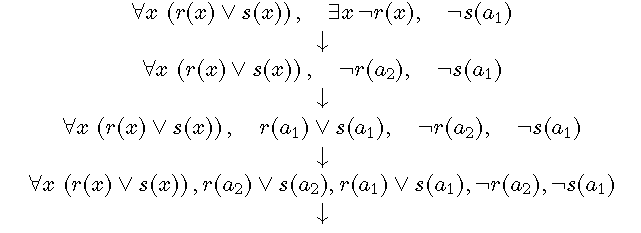
语义树并不能判定所有一阶逻辑公式的可满足性,但可以证明一个不可满足式的不可满足性。

如果一个逻辑公式是永真的, 那么可以通过建立该公式的否的语义树来证明。

一阶逻辑的金琛系统：

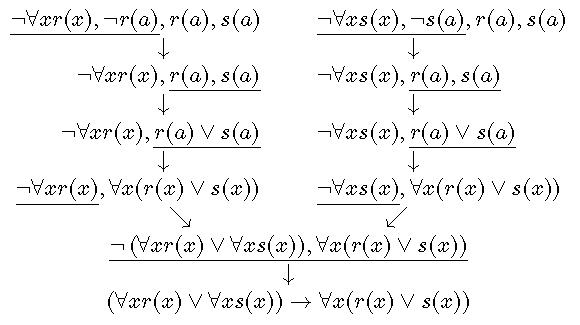
一阶逻辑的希尔伯特系统:

公理 1: $⊢(A\to (B\to A))$${\vdash} (A\rightarrow(B\rightarrow A))$

公理 2: $⊢(A\to (B\to C))\to ((A\to B)\to (A\to C))$$\vdash (A\rightarrow (B \rightarrow C)) \rightarrow ((A\rightarrow B) \rightarrow (A\rightarrow C))$

公理 3: $⊢(\mathrm{\neg }B\to \mathrm{\neg }A)\to (A\to B)$$\vdash (\lnot B \rightarrow \lnot A) \rightarrow (A \rightarrow B)$

公理 4: $⊢\mathrm{\forall }xA(x)\to A(a)$$\vdash \forall xA(x) \rightarrow A(a)$

公理 5: $⊢\mathrm{\forall }x(A\to B(x))\to (A\to \mathrm{\forall }xB(x)).$$\vdash \forall x(A \rightarrow B(x)) \rightarrow (A \rightarrow \forall xB(x)).$

假言推理(Modus Ponens): $\frac{⊢A\to B⊢A}{⊢B}$$\frac{\vdash A \rightarrow B\hspace{1em}\vdash A}{\vdash B}$

泛化: $\frac{⊢A(a)}{⊢\mathrm{\forall }xA(x)}.$$\frac{\vdash A(a)}{\vdash \forall xA(x)}.$

对谓词公式$A(x)$$A(x)$来说,在量词$\mathrm{\forall }y$${\forall}y$或$\mathrm{\exists }y$${\exists}y$的辖域内,如果没有$x$$x$的自由变量,则称$A(x)$$A(x)$对于变量$y$$y$是自由的。

例: 令$A(x)$$A(x)$表示下列谓词公式:

(1) $A(x)=\mathrm{\forall }yP(y)\vee Q(x,y)$$A(x)={\forall}yP(y){\vee}Q(x,y)$

(2) $A(x)=\mathrm{\forall }yP(y)\to (Q(x)\wedge Q(y))$$A(x)={\forall}yP(y){\rightarrow}(Q(x){\wedge}Q(y))$

(3) $A(x)=\mathrm{\forall }yP(\boxed{{\displaystyle x}},y)\to Q(x,y)$$A(x)={\forall}yP(\boxed{x},y){\rightarrow}Q(x,y)$

(4) $A(x)=\mathrm{\forall }y(P(y)\vee Q(\boxed{{\displaystyle x}},y))$$A(x)={\forall}y(P(y){\vee}Q(\boxed{x},y))$

(5) $A(x)=\mathrm{\forall }y(P(y)\vee \mathrm{\forall }xQ(x,y))$$A(x)={\forall}y(P(y){\vee}{\forall}xQ(x,y))$

其中(1),(2)和(5)对$y$$y$是自由的,(3)和(4)对$y$$y$不是自由的。

公理4也可以转化为规则, 称存在量词具体化规则(Universal Specification), 简称US规则。

其中$c$$c$为个体域中任意个体常量。

这里要求$A(x)$$A(x)$对$y$$y$是自由的, $y$$y$或$c$$c$是取代了$A(x)$$A(x)$中所有自由出现的$x$$x$.

例: 设个体域为实数集合,$L(x,y)$$L(x,y)$表示$x<y$$x<y$,则$\mathrm{\exists }x\mathrm{\exists }yL(x,y)$${\exists}x{\exists}yL(x,y)$解释为"对任一实数$x$$x$,都存在实数$y$$y$,使得$x<y$$x<y$",这是一个真命题。

推导过程如下:

1.$⊢\mathrm{\forall }x\mathrm{\exists }yL(x,y)$${\vdash\,}{\forall}x{\exists}yL(x,y)\qquad$ Assumption

2.$⊢\mathrm{\exists }yL(y,y)$${\vdash\,}{\exists}yL(y,y)\qquad$ US,1

出错的原因是$\mathrm{\exists }yL(x,y)$${\exists}yL(x,y)$对$y$$y$不是自由的。

全称量词泛化规则(Universal Generalization)又称全称量词引入规则, 简称UG规则。

全称量词泛化规则要求: 前提$A(x)$$A(x)$对于$x$$x$的任意取值都成立, $A(x)$$A(x)$对$y$$y$是自由的, 且取代$x$$x$的个体变量$y$$y$不能在$A(x)$$A(x)$中约束出现。

例: 设个体域为实数集合, $L(x,y)$$L(x,y)$表示$x<y$$x<y$, 推导过程如下:

1.$⊢\mathrm{\forall }x\mathrm{\exists }yL(x,y)$${\vdash\,}{\forall}x{\exists}yL(x,y)\qquad$ Assumption

2.$⊢\mathrm{\exists }yL(z,y)$${\vdash\,}{\exists}yL(z,y)\qquad\qquad$ US,1

3.$⊢\mathrm{\forall }y\mathrm{\exists }yL(y,y)$${\vdash\,}{\forall}y{\exists}yL(y,y)\qquad$ UG,2

出错的原因是用在$\mathrm{\exists }yL(z,y)$${\exists}yL(z,y)$中约束出现的$y$$y$取代了$z$$z$.

其它规则

存在量词具体化规则(Existential Specification), 简称ES规则, 也称C-Rule.

其中$c$$c$为特定的个体常量,且使用不曾在$A(x)$$A(x)$中出现过的个体常量$c$$c$或个体变量$y$$y$取代$x$$x$.

当$A(x)$$A(x)$中存在其他自由变量时不宜使用此规则。

例: 设个体域为实数集合,$L(x,y)$$L(x,y)$表示$x<y$$x<y$,推导过程如下:

1.$⊢\mathrm{\forall }x\mathrm{\exists }yL(x,y)$${\vdash\,}{\forall}x{\exists}yL(x,y)\qquad$ Assumption

2.$⊢\mathrm{\exists }yL(z,y)$${\vdash\,}{\exists}yL(z,y)\qquad\,\,\,$ US,1

3.$⊢L(z,c)$${\vdash\,}L(z,c)\qquad\qquad$ ES,2

出错原因是$\mathrm{\exists }yL(z,y)$${\exists}yL(z,y)$中存在自由变量$z$$z$,不宜使用ES规则。

存在量词泛化规则, 简称EG (Existential Generalization)规则。

其中$c$$c$为特定的个体常量, $A(x)$$A(x)$对$y$$y$是自由的, 取代$c$$c$的个体变量$y$$y$不曾在$A(x)$$A(x)$中出现, 且$y$$y$不能是$A(x)$$A(x)$中的个体变量。

例: 设个体域为实数集合,$L(x,y)$$L(x,y)$表示$x<y$$x<y$,推导过程如下:

1.$⊢\mathrm{\exists }xL(x,0)$${\vdash\,}{\exists}xL(x,0)\qquad\qquad$ Assumption

2.$⊢\mathrm{\exists }x\mathrm{\exists }xL(x,x)$${\vdash\,}{\exists}x{\exists}xL(x,x)\qquad$ EG,1

出错原因是$x$$x$已在$\mathrm{\exists }xL(x,0)$${\exists}xL(x,0)$中出现, 此时不能用$x$$x$取代0.

定理: $\mathrm{\forall }x(A(x)\to B(x))\to (\mathrm{\forall }xA(x)\to \mathrm{\forall }xB(x)).$${\forall}x(A(x){\rightarrow}B(x)){\rightarrow}({\forall}xA(x){\rightarrow}{\forall}xB(x)).$

证明:

1.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢\mathrm{\forall }xA(x)$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}{\forall}xA(x)$ Assumption

2.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢A(a)$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}A(a)$ A4,1

3.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢\mathrm{\forall }x(A(x)\to B(x))$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}{\forall}x(A(x){\rightarrow}B(x))$ Assumption

4.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢A(a)\to B(a)$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}A(a){\rightarrow}B(a)$ A4,3

5.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢B(a)$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}B(a)$ MP,2,4

6.$\mathrm{\forall }x(A(x)\to B(x)),\mathrm{\forall }xA(x)⊢\mathrm{\forall }xB(x)$${\forall}x(A(x){\rightarrow}B(x)), {\forall}xA(x){\vdash}{\forall}xB(x)$ UG,5

7.$\mathrm{\forall }x(A(x)\to B(x))⊢\mathrm{\forall }xA(x)\to \mathrm{\forall }xB(x)$${\forall}x(A(x){\rightarrow}B(x)){\vdash}{\forall}xA(x){\rightarrow}{\forall}xB(x)$ Deduction,1,6

8.$⊢\mathrm{\forall }x(A(x)\to B(x))\to (\mathrm{\forall }xA(x)\to \mathrm{\forall }xB(x))$${\vdash}{\forall}x(A(x){\rightarrow}B(x)){\rightarrow}({\forall}xA(x){\rightarrow}{\forall}xB(x))$ Deduction,3,7