符号化与一阶公式

情形1:

1. 一个人的姥姥或者母亲是一个人的先辈

2. 一个人的先辈的先辈是这个人的先辈

3. 张三是李四的姥姥,李四是王五的母亲

4. 所以张三是王五的先辈

情形2:

1. 一个数的平方或立方是一个数的幂

2. 一个数的幂的幂是一个数的幂

3. 64是8的平方, 8是2的立方

4. 所以64是2的幂

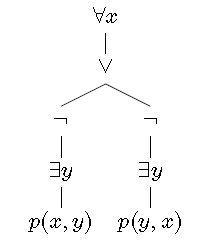
两种情形可统一符号化为:

1. $\mathrm{\forall }x\mathrm{\forall }y((p(y,x)\vee q(y,x))\to r(y,x))$$\forall x\forall y((p(y,x){\lor}q(y,x))\rightarrow r(y,x))$​

2. $\mathrm{\forall }x\mathrm{\forall }y(\mathrm{\exists }z(r(y,z)\wedge r(z,x))\to r(y,x))$$\forall x\forall y(\exists z(r(y,z)\land r(z,x))\rightarrow r(y,x))$

3. $p(a,b)\wedge q(b,c)$$p(a,b)\land q(b,c)$​

4. $r(a,c)$$r(a,c)$​

与命题逻辑相比,一阶逻辑引入了:

• 变量, 如$x$$x$和$y$$y$, 可以表示任意多的常量。
• 关系, 如$p(y,x)$$p(y,x)$和$q(y,x)$$q(y,x)$.

一阶逻辑(First-Order Logic)或谓词逻辑(Predicate Logic):

1.逻辑联结词

• $\vee ,\wedge ,\to ,\leftrightarrow ,\cdots$$\lor,\land,\rightarrow,\leftrightarrow,\cdots$.

2.个体常量

• $a$$a$: 小明; $b$$b$: 猫。

3.个体变量:

• $x$$x$可以是小明($a$$a$),也可以是猫($b$$b$).

4.个体域(Domain of Discourse):

• 通常用$D$$D$表示。
• $\mathrm{\exists }x\mathrm{\exists }y\mathrm{\exists }z(x^3+y^3=z^3)$${\exists}x{\exists}y{\exists}z\,(x^3+y^3=z^3)$针对不同的个体域(正整数和正实数)差别明显。

5.谓词 (Predicates,本质上是关系)

• $S(x)$$S(x)$: $x$$x$是大学生。
• $S(?)$$S(?)$: $\cdots$${\cdots}$是大学生。
• $Q(a,b)$$Q(a,b)$: 小明($a$$a$)喜欢猫($b$$b$).
• $Q(?,?)$$Q(?,?)$: $\cdots$${\cdots}$喜欢$\cdots$${\cdots}$.
• $G(a,b,c)$$G(a,b,c)$: 上海位于北京和广州之间。
• $G(?,?,?)$$G(?,?,?)$: $\cdots$${\cdots}$位于$\cdots$${\cdots}$和$\cdots$${\cdots}$之间。
• 表示$n$$n$个个体之间关系$P(x_1,x_2,\cdots ,x_n$$P(x_{1},x_{2},{\cdots},x_{n}$)的谓词称为$n$$n$元谓词。

6.函数或函词

• $f(x,y,z)=x^2+y^2-z^2$$f(x,y,z)=x^2+y^2-z^2$.
• 有利于谓词的表达,如$P(f(x,y,z),0)$$P(f(x,y,z),0)$.

7.量词(Quantifier)

• $\mathrm{\forall }$$\forall$, $\mathrm{\exists }$$\exists$.

8.辖域或作用域(Scope)

• $\mathrm{\forall }x(P(x)\to \mathrm{\exists }yQ(x,y,z))\wedge R(x)$${\forall}x(P(x){\rightarrow}{\exists}yQ(x,y,z)){\wedge}R(x)$.
• $\mathrm{\forall }x(P(x,y)\wedge Q(y))\to \mathrm{\exists }yR(x,y)$${\forall}x(P(x,y){\wedge}Q(y)){\rightarrow}{\exists}yR(x,y)$.

符号化应与自然语言的本意相符。

• "所有$A$$A$都是$B$$B$"形式的命题通常符号化为$\mathrm{\forall }x(A(x)\to B(x))$${\forall}x(A(x){\rightarrow}B(x))$.
• "有一些$A$$A$是$B$$B$"形式的命题通常符号化为$\mathrm{\exists }x(A(x)\wedge B(x))$${\exists}x(A(x){\wedge}B(x))$.

谓词公式实例:

• $\mathrm{\forall }x(\mathrm{\neg }\mathrm{\exists }yp(x,y)\vee \mathrm{\neg }\mathrm{\exists }yp(y,x))$$\forall x(\lnot \exists yp(x, y)\lor \lnot \exists yp(y, x))$​.

令$P$$P$是$n$$n$元谓词,$x_1,x_2,\cdots ,x_n$$x_{1},x_{2},{\cdots},x_{n}$是个体变量或个体常量,则$P(x_1,x_2,\cdots ,x_n)$$P(x_{1},x_{2},{\cdots},x_{n})$称为原子谓词公式.

特别地,当$n=0$$n=0$时,原子谓词公式$P(x_1,x_2,\cdots ,x_n)$$P(x_{1},x_{2},{\cdots},x_{n})$就是$P$$P$,此时的原子谓词公式可以看作0元谓词。

复合谓词公式:由量词和逻辑联结词将原子谓词公式联结组成的谓词公式。

若$P(x,y,z):x^3+y^3=z^3$$P(x,y,z): x^3+y^3=z^3$, $P(x,y,z)$$P(x,y,z)$是原子谓词公式, 而$\mathrm{\exists }x\mathrm{\exists }y\mathrm{\exists }zP(x,y,z)$${\exists}x{\exists}y{\exists}z\,P(x,y,z)$是符合谓词公式。

谓词公式递归定义如下:

(1) 原子谓词公式是谓词公式;

(2) 如果$A$$A$是谓词公式,则$\mathrm{\neg }A$${\lnot}A$也是谓词公式;

(3) 如果$A,B$$A,B$是谓词公式,则$A\wedge B,A\vee B,A\to B$$A{\wedge}B,A{\vee}B,A{\rightarrow}B$和$A\leftrightarrow B$$A{\leftrightarrow}B$也是谓词公式;

(4) 如果$A$$A$是谓词公式,$x$$x$是个体变元,则$\mathrm{\forall }xA$${\forall}xA$和$\mathrm{\exists }xA$${\exists}xA$也是谓词公式;

(5) 有限次使用规则(1)-(4)所得到的由原子谓词公式、逻辑联结词、量词和圆括号组成的符号串才是谓词公式。

形式化描述:

1. $arg::=xx\in V$$arg ::=x \,\,x \in V$
2. $arg::=aa\in A$$arg ::=a \,\,a \in A$
3. $arglist::=arg$$arg\,list ::= arg\,\,$
4. $arglist::=arg,arglist$$arg\,list ::= arg,\,arg\,list\,\,$
5. $atomicwff::=p(arglist),p\in P,n\ge 1$$atomic\,wff ::=p(arg\,list),\,\,p\in P,\,\,n\ge 1$
6. $wff::=atomicwff$$wff ::= atomic\,wff\,\,$
7. $wff::=\mathrm{\neg }wff$$wff ::= \lnot\,wff\,\,$
8. $wff::=wff\circ wff,\circ :\vee ,\wedge ,\uparrow \cdots$$wff ::= wff\,\circ\,wff,\,\,\,\circ:\,\,\lor,\land,\uparrow\cdots$
9. $wff::=\mathrm{\forall }xwff,x\in V$$wff ::= \forall x\,wff,\,\,\,x \in V$
10. $wff::=\mathrm{\exists }xwff,x\in V$$wff ::= \exists x\,wff,\,\,\,x \in V$

变量分约束(Bound)变量和自由(Free)变量两种。

在$\mathrm{\forall }yP(x,y)$$\forall y\, P(x,y)$中,$x$$x$是自由变量,$y$$y$是约束变量。

在$\mathrm{\forall }x\mathrm{\forall }y(P(x)\to Q(x,f(y),z))$${\forall}x{\forall}y(P(x)\rightarrow Q(x,f(y),z))$中, $x$$x$和$y$$y$是约束变量, $z$$z$是自由变量。

在$R(x)\to \mathrm{\forall }xT(x)$$R(x)\rightarrow{\forall}x\,T(x)$中,$x$$x$既是自由变量又是约束变量。也可以说,第一个$x$$x$是自由变量,第二个$x$$x$是约束变量。

没有自由变量的一阶逻辑公式称为一阶逻辑语句(First-Order Sentence)。