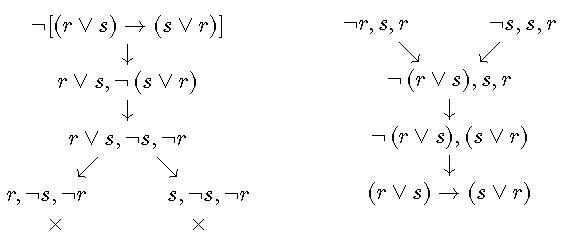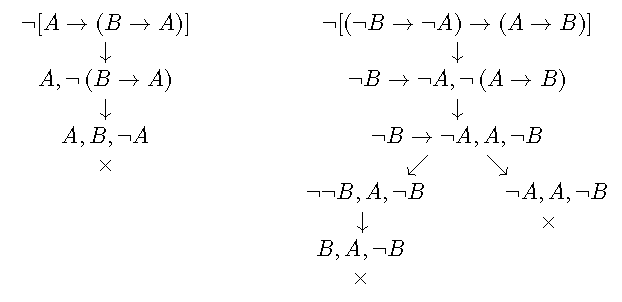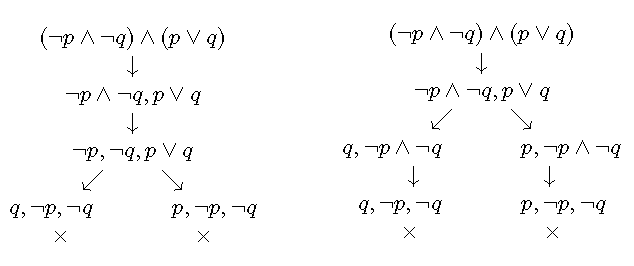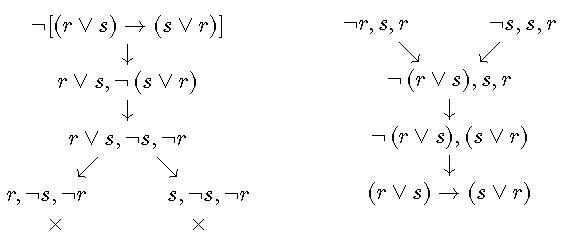语义树与金琛系统
一个文字(Literal)是一个原子命题或者一个原子命题的否。
原子命题称为正文字, 原子命题的否称为负文字。
对于任意的原子命题, 称为一对互补文字。
定理: 一组文字是可满足的, 当且仅当这组文字中不包含互补文字。
例如: 中, 和是正文字, 和是负文字, 和是一对互补文字。因为包含一对互补文字,所以是不可满足的。

借助-公式建立语义树。
-公式
-公式
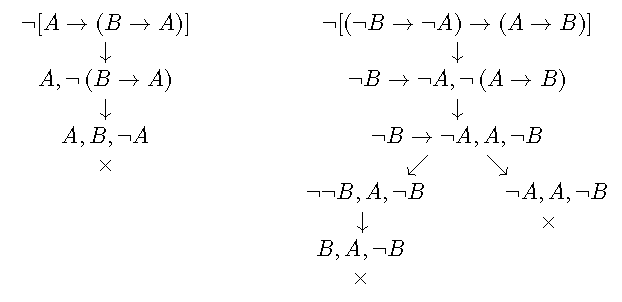
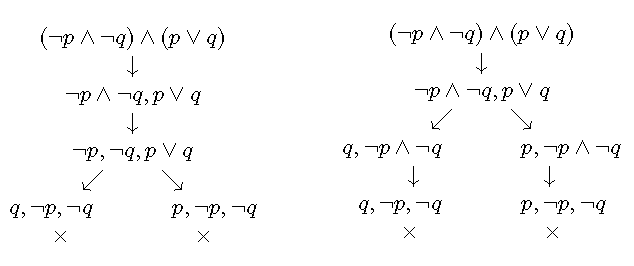
如果一个语义树的所有分支都是不可满足的,称该语义树是不可满足的。否则, 称该语义树是可满足的。
定理(完备性, Completeness): 如果一个公式是永真的,那么的语义树是不可满足的。
定理(可靠性, Soundness): 如果一个公式的否的语义树是不可满足的,那么这个公式是永真的。
定理: 一个公式是永真的, 当且仅当的语义树是不可满足的。
金琛系统(Gentzen System, )是一个证明系统。金琛系统从不可满足的若干组文字出发, 根据和规则逐步推导, 最终证明命题。
通过系统证明:.
证明:.