可计算性

一个由自然数构成的集合是可计算的(Computable, 或可判定的、递归的、图灵可计算的)是指: 给定一个$n$$n$, 存在一个图灵机, 如果$n$$n$在这个集合, 那么图灵机能终止并输出1; 如果$n$$n$不在这个集合, 那么图灵机能终止并输出0.

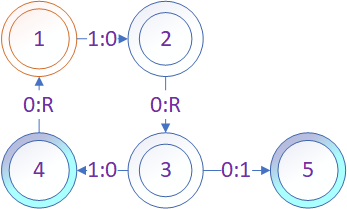
例如: 偶数集合是可计算机集合。存在奇偶校验图灵机,使得当输入为偶数时图灵机终止并输出1;当输入为奇数时图灵机终止并输出0.

一个函数$f:N\to N$$f:N{\rightarrow}N$是可计算的是指: 存在一个图灵机, 给定任意一个输入$n$$n$, 都能得到一个输出$f(n)$$f(n)$.

换句话说，如果存在一段程序来计算一个函数，那么这个函数就是可计算的。

例如: 前面我们通过图灵机实现的$f(x)=2x$$f(x)=2x$就是可计算的函数。

一个语言是可判定的(Decidable, 或Recursive ),如果有一个图灵机能接受所有属于该语言的字串,并拒绝所有不属于该语言的字串。

也就是说,对于所有输入,该图灵机都可以停机。

可判定语言的交、并和补也是可判定语言。

一个语言是可识别的(Recognizable, 或Recursively Enumerable):如果有一个图灵机能接受所有属于该语言的字串,并停机;但是对于不属于该语言的字串,该图灵机可能不停机。

可识别语言的交与并也都是可识别语言。

当且仅当一个语言和它的补都是可识别语言,这个语言是可判定语言。

可判定语言都是可识别语言,反之未必。

是否存在一种语言是可识别语言,但不是可判定语言呢？

答案是肯定的。

例如: 停机问题就是最早出现的一个实例。

停机问题(Halting Problem):

给定一个图灵机$T$$T$，和一个任意语言(程序)集合$S$$S$，是否$T$$T$会最终停止于每一个$s\in S$$s{\in}S$?

例如:死循环就停不了机。

通俗的说，停机问题就是判断任意一个程序是否会在有限的时间之内结束运行的问题。

用反证法证明(类似对角化方法):

假设有个函数Halt(P,x)能解决停机问题. 对于所有输入Halt(P,x),如果P(x)能停机返回True,如果P(x)不停机返回False,反正Halt(P,x)都能停机。

定义Sly(P):

1.运行Halt(P,P).该程序总会停机并返回一个结果.

2.如果这个结果为True,那么永远循环(loop);否则停机.

也就是说,如果P(P)能停机,Sly(P)将不停机;如果P(P)不停机,Sly(P)将停机.

现在运行Sly(Sly).具体地,它首先运行Halt(Sly,Sly),该程序能停机并返回结果.

如果这个结果是True,则不停机;否则停机.(根据sly函数的定义)

于是: 如果Sly(Sly)停机,那么Halt(Sly,Sly)返回True,则Sly(Sly)不停机;

反之,Sly(Sly)不停机,Halt(Sly,Sly)返回False,则Sly(Sly)停机.

其它一些已证的不可判定问题:

Post Correspondence Problem

Rice's theorem

Hilbert's tenth problem (确定丢番图方程是否有整数解)

Group isomorphism problem

通用图灵机(Universal Turing Machine)是一种图灵机，它能模拟任何输入的任何图灵机。

如果一个计算机系统能模拟一个通用图灵机，称它是图灵完全的(Turing-Complete).

根据邱奇-图灵定理(Chuch-Turing Thesis)可知，通用图灵机可以计算任何可计算函数。所以图灵完全的计算机系统也可以计算任何可计算函数。

事实上,通用图灵机也能够接受可判定语言和可识别语言。

以下这些系统(或语言)都是图灵完全的:

• Fortran, Pascal, C, C++, Java, Python, Go等等。

此外, 不可识别的语言也是存在的。

其它一些相关概念：

• 可定义语言(Definable Language)
• 可归约性(Reducibility)
• 复杂性(Complexity)