有限状态机

有限状态机(Finite-State Machine, FSM)是表示有限个状态以及在这些状态之间的转移和动作等行为的计算模型。

一个确定性有限状态机(Deterministic Finite Automata, DFA) 是一个五元组($\mathrm{\Sigma },S,s_0,\delta ,F$$\Sigma, S, s_0, \delta, F$),其中:

• $\mathrm{\Sigma }$$\Sigma$ 是输入字符集(有限、非空).
• $S$$S$是有限非空的状态集。
• $s_0$$s_0$是初始状态,属于集合$S$$S$.
• $\delta$$\delta$是状态转移函数 $\delta :S\times \mathrm{\Sigma }\to S$$\delta: S \times \Sigma \rightarrow S$.
• $F$$F$是终止状态,也属于集合$S$$S$。

正则表达式(Regular Expression, RE)由一组字符集$\mathrm{\Sigma }$$\Sigma$通过连接、并、克莱尼(Kleene)闭包等运算得到。RE用来描述正则语言(regular languages, RL)或正则集合。

正则表达式的正式定义如下：

1. 空集$\varphi$$\phi$是RE,对应于空语言。
2. 空串$ϵ$$\epsilon$是RE,没有实际字符,仅包含一个空字符。对应于空字符串语言。
3. 每一个字符$a\in \mathrm{\Sigma }$$a\in\Sigma$是RE,是单字符串。对应单字符串语言。
4. 如果$r$$r$和$s$$s$是RE,那么$(rs)$$(rs)$, $(r+s)$$(r + s)$, 和$(r^{\ast })$$(r^*)$也是RE.对应$R\cdot S$$R{\cdot}S$, $R\cup S$$R{\cup}S$和$R^{\ast }$$R^*$语言。

克莱尼闭包:

{"a","bc"}${}^{\ast }$$^*$={$ϵ$$\epsilon$,"a","bc","abc","bca","bcbc","aa","bcbcbc","abcbc",$\cdots$$\cdots$}

语言(languages)，无论是正则语言还是非正则语言，通常都用某种形式的二进制串来表示。

例如：第一个字符是0的语言，可以包括001,011,1,01001等符合该语言的字符串。 而110,10001,1等字符串不属于该语言。

不同的表达式有可能表达的是同一个语言。

例: $((0^{\ast })(1))((1)(0^{\ast })(1)+0{)}^{\ast }$$((0^*)(1))((1)(0^*)(1)+0)^*$和 $0^{\ast }1({10}^{\ast }1+0{)}^{\ast }$$0^*1(10^*1+0)^*$表达的语言相同。

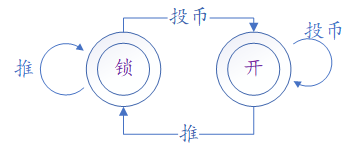
有限状态机可以产生或接受(Accept)正则语言。

这里的字符串中的字符相当于之前例子中的"投币"和"推"。

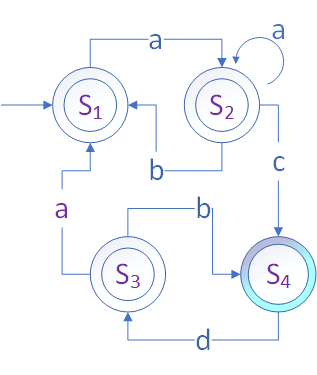
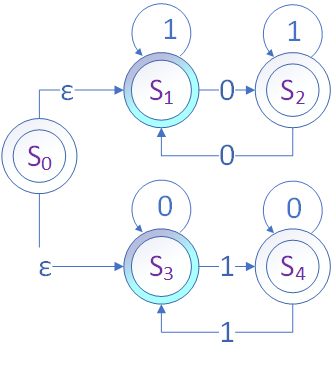
有两个办法来建立有限状态机与语言的联系。

• 反复从起始状态运行到终止状态，看看此有限状态机能生成哪些串？
• 给定一类字符串，看看有限状态机是否能按照字符串走到终止状态。

特别需要注意的是: 并非所有的语言都是正则语言。

例如: $L_1=\{0^p{1}^p|p\ge 1\}$$L_1=\{0^p1^p\,|\,p{\ge}1\}$和$L_2=\{a^{n}b{a}^n|n\ge 1\}$$L_2=\{a^nba^n\,|\,n{\ge}1\}$不是正则语言。

通常, 有两种类型的有限状态机:确定性(Deterministic)有限状态机和非确定性(Non-Deterministic)有限状态机(NDFAs)。

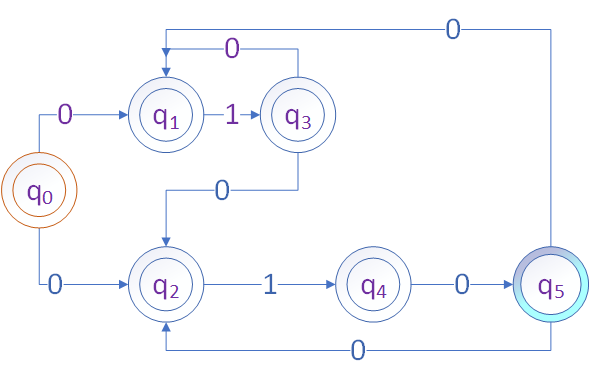
事实上非确定性有限状态机与确定性有限状态机(DFAs)是等价的。

• DFA可以看作NDFA的一个子集, 所以DFA转换成NDFA不成问题。
• NDFA转换成DFA: 如果NDFA用到$n$$n$个状态,转化后的DFA需要$2^n$$2^n$个状态。例如NDFA有3个状态，DFA就可以使用$\{\mathrm{\varnothing },\{a\},\{b\},\{c\},\{a,b\},$$\{\emptyset, \{a\},\{b\},\{c\},\{a,b\},$ $\{a,c\},\{b,c\},\{a,b,c\}\}$$\{a,c\},\{b,c\},\{a,b,c\}\}$来穷尽这些状态。

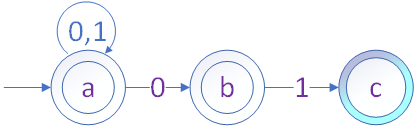
在非确定性状态机中$\delta :S\times \mathrm{\Sigma }\to \mathcal{P}(S)$$\delta: S \times \Sigma \rightarrow \mathcal{P}(S)$, 例如$\delta$$\delta$可能对于相同的输入进入不同的下一个状态。

有限状态机与图灵机之间的关系:

1.有限状态机可以看作是一个受限的图灵机：

• 只能读不能写
• 只能往单方向走

2.有限状态机也是图灵机的一部分。